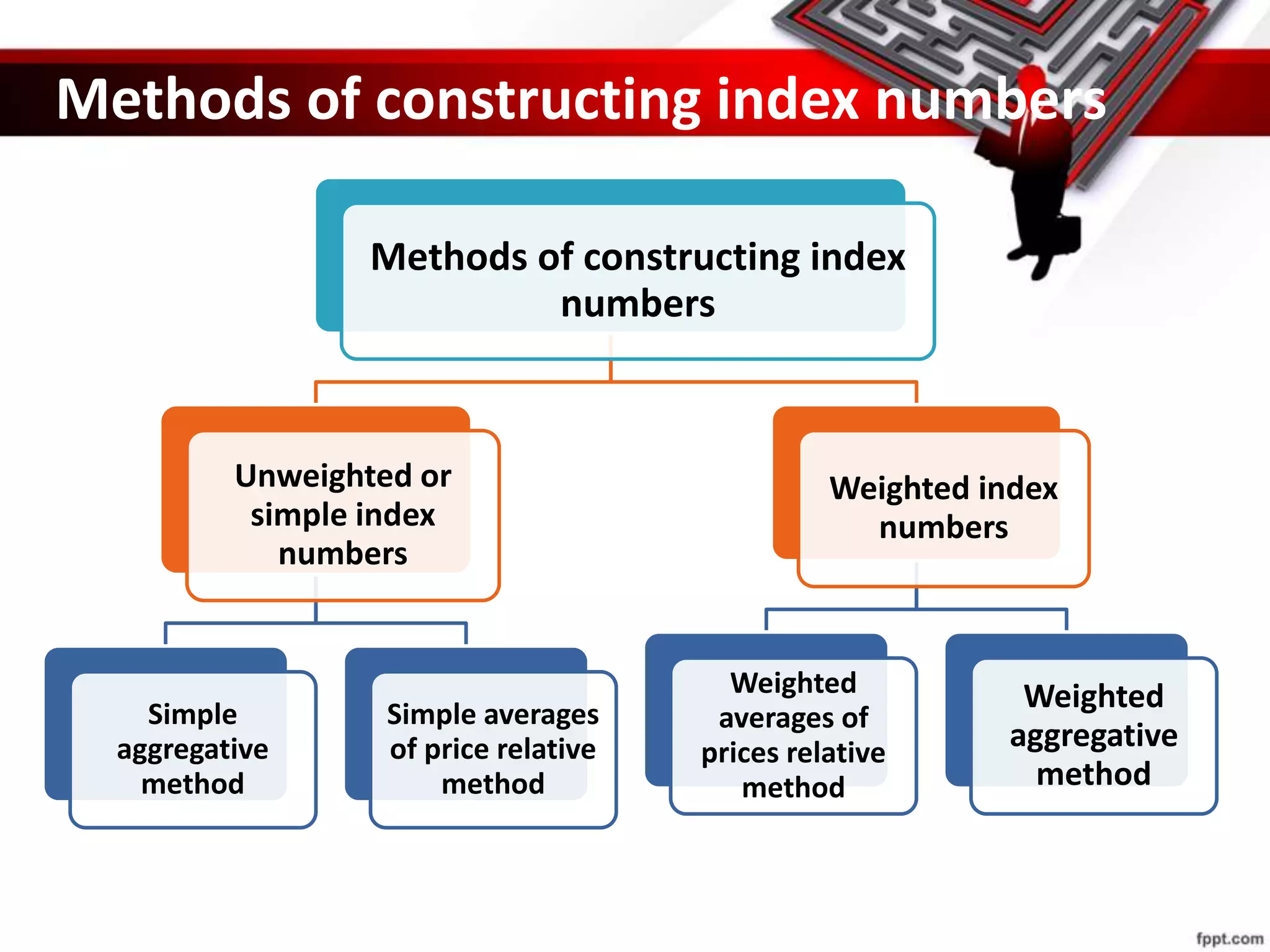
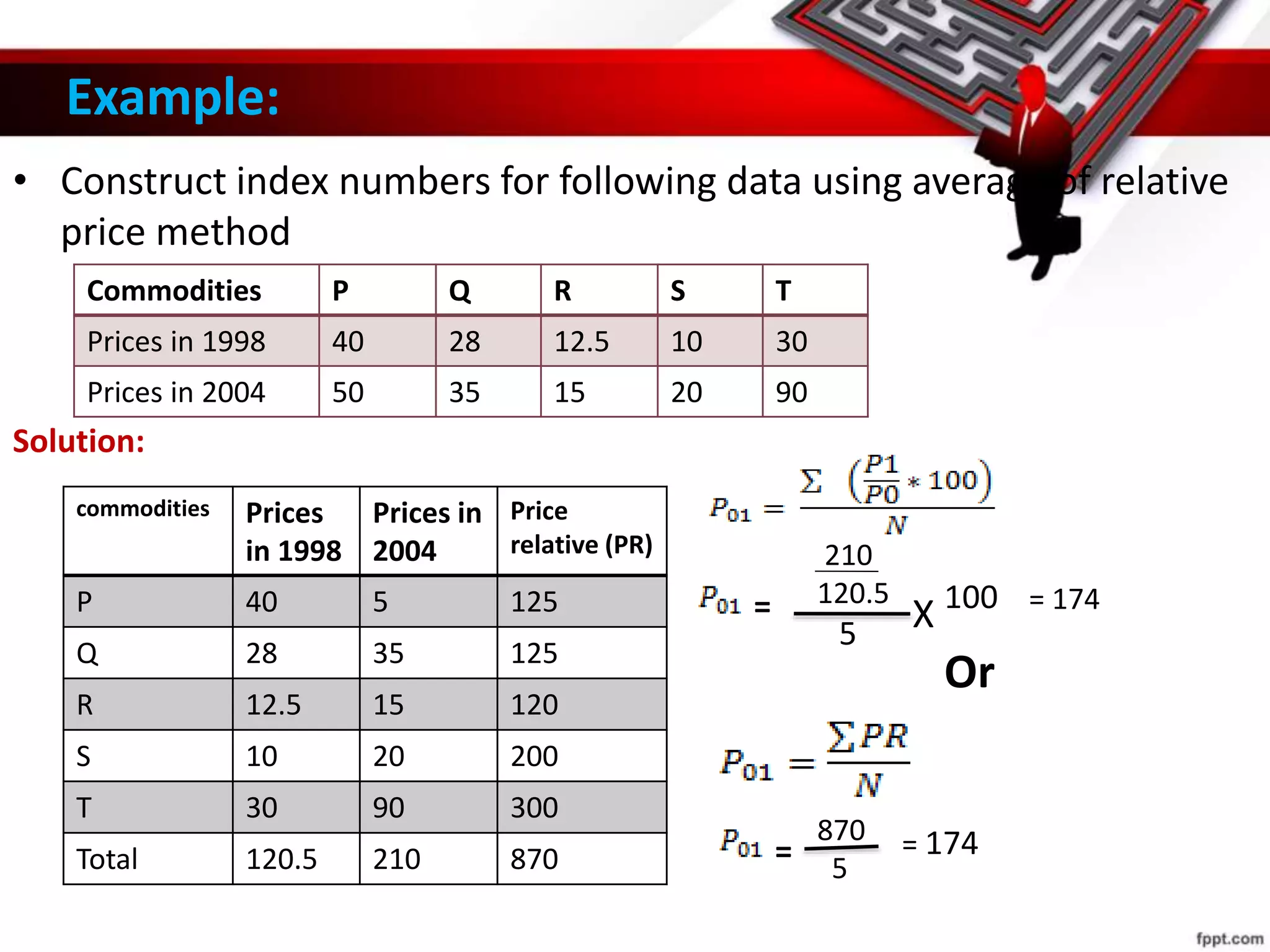
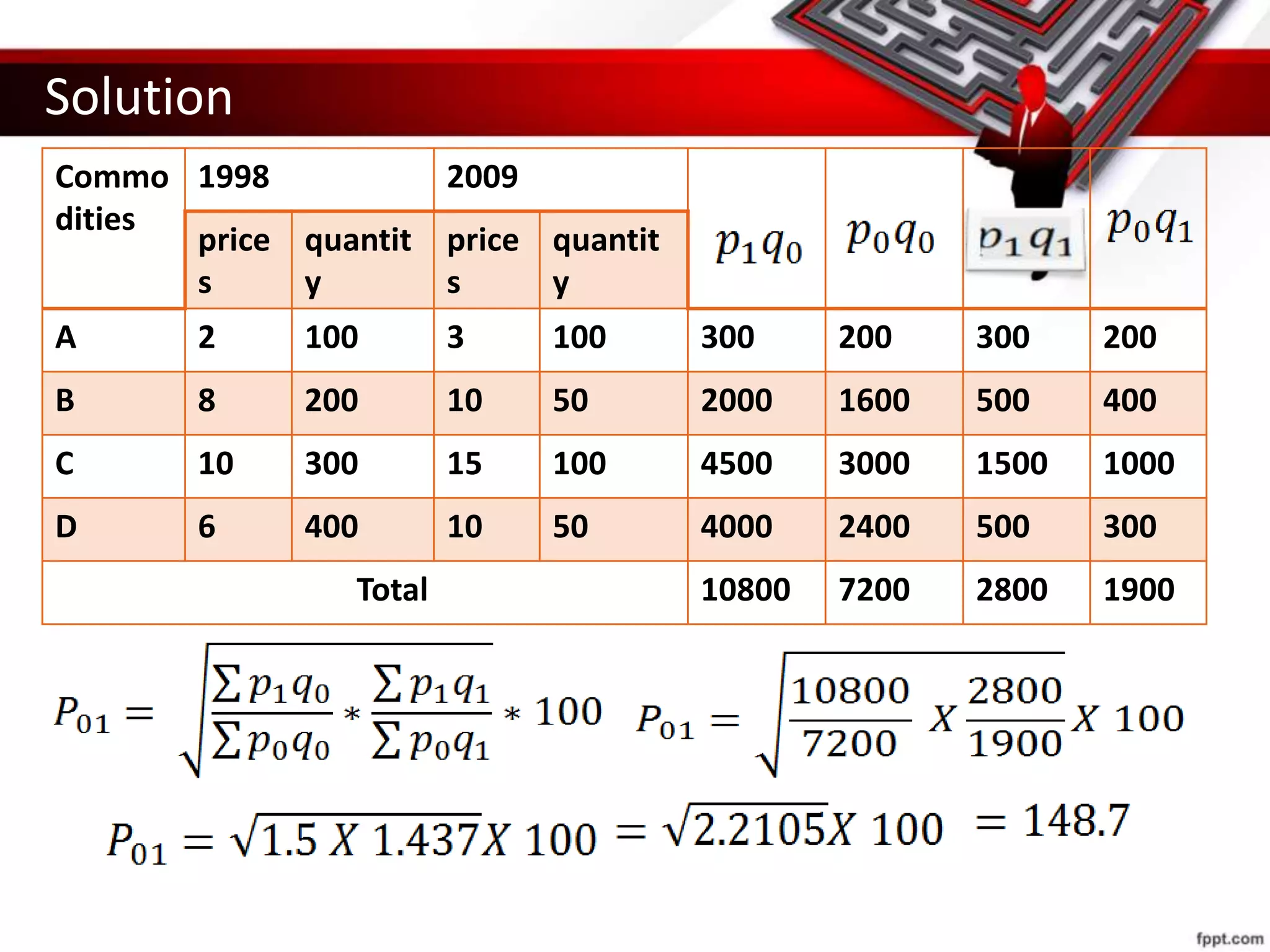
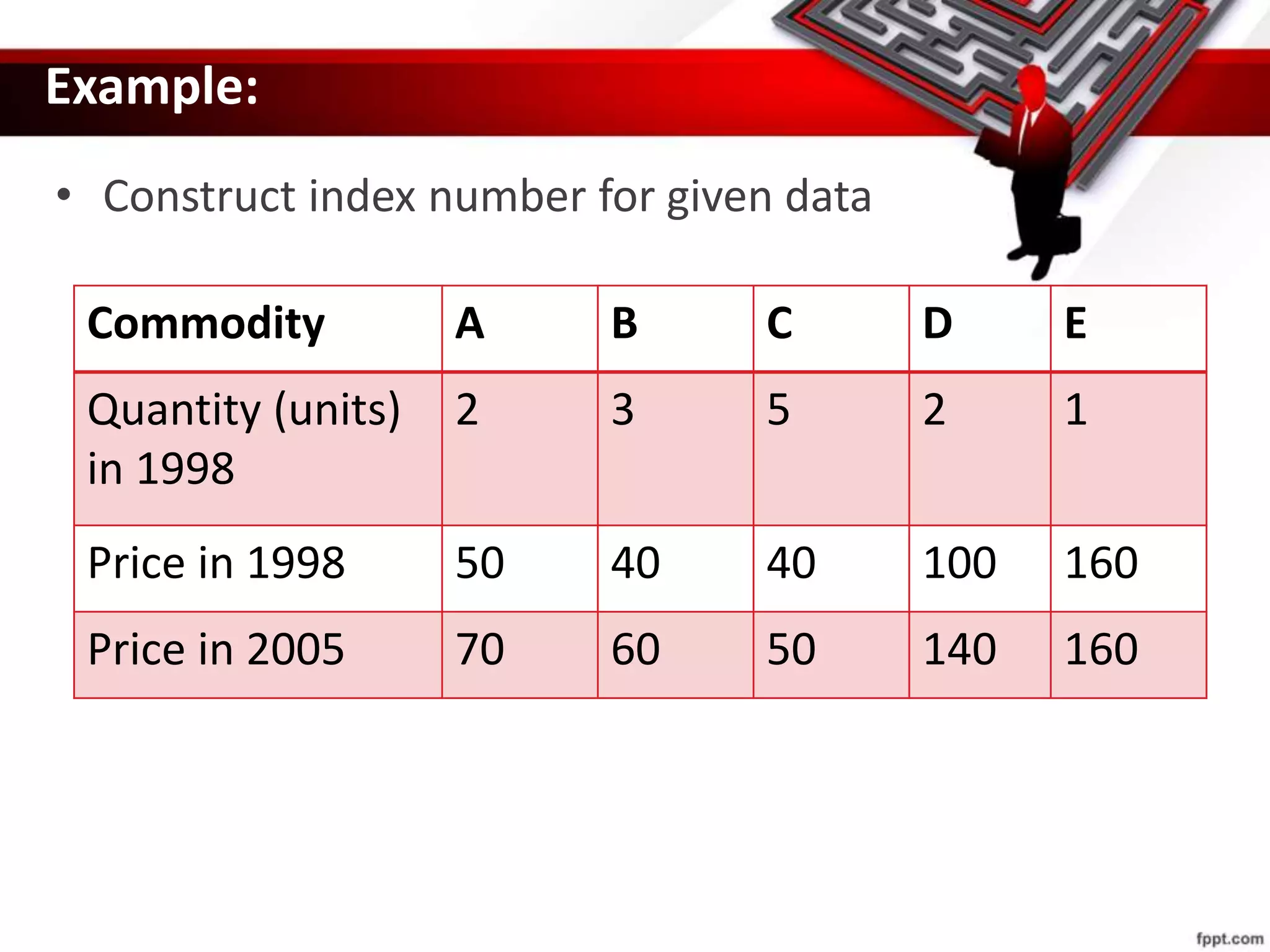
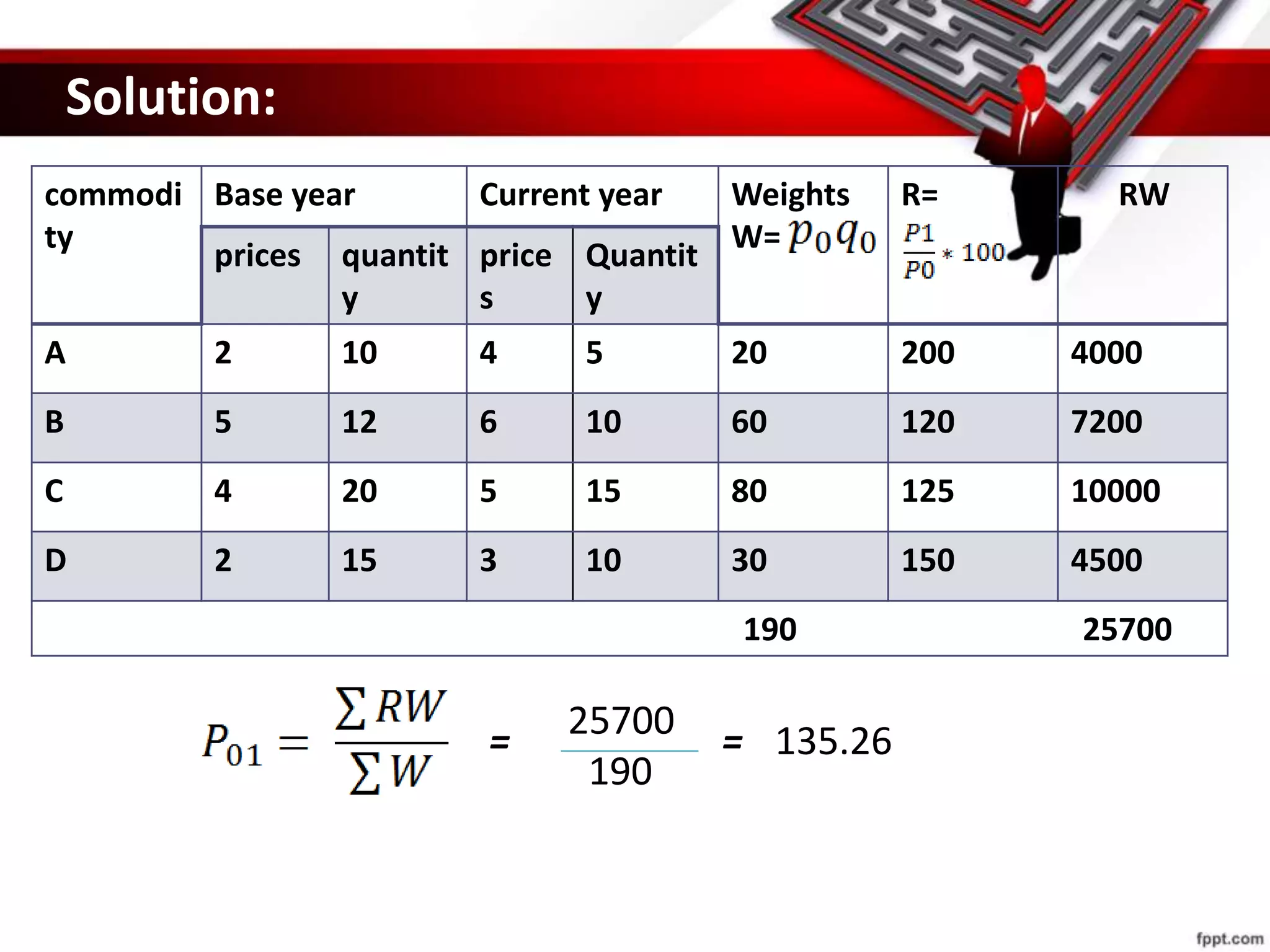
This document provides an overview of index numbers, including their meaning, features, advantages, limitations, construction methods, and examples of important index numbers. Index numbers are statistical measures used to compare economic variables, like prices or production, over time. They show percentage changes from a base period and are widely used by governments, businesses, and economists to understand inflation trends and formulate policies. The document discusses various methods for constructing index numbers, such as Laspeyre's method, Paasche's method, and Fisher's method which involve assigning weights. Important commonly used index numbers mentioned include the Consumer Price Index, Sensex, Agricultural Production Index, and Wholesale Price Index.