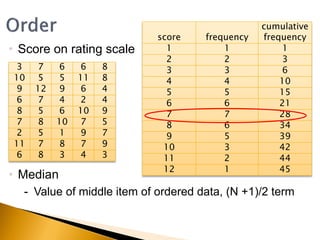
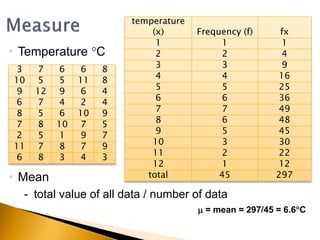
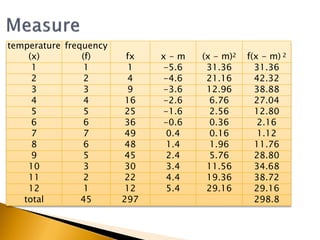
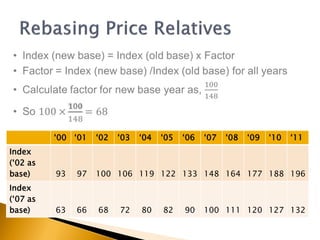
The document provides an overview of fundamental management statistics, covering data types (nominal, ordinal, interval, and ratio) and essential summary statistics (mode, median, mean, etc.). It teaches students how to calculate important index numbers and use them for percentage changes and data deflation. Additionally, it illustrates how to analyze and interpret different data types through various examples and calculations.

1. Topic 1:
Introductory Management Statistics

2. This topic will cover:
◦ Data types
◦ A revision of summary statistics
◦ Index numbers

3. By the end of this topic students will be able
to:
◦ recognise nominal, ordinal, interval and ratio data
types
◦ recognise and use mode, median, mean, range,
standard deviation and coefficient of variation
◦ calculate Laspeyres and Paasche index numbers
◦ use index numbers to calculate percentage changes
and to deflate series

4. ◦ Nominal
◦ Ordinal
◦ Interval
◦ Ratio
Information Content
High
Low

5. ◦ Data which is only categorised (group characteristic)
 Count but not order, nor measure nor ratio
◦ Examples
 Gender (male or female)
 Job role (administration, production, accounting,
sales)
 Product type (fruit cake, chocolate cake, cream
cake)
◦ Summary statistics
 Mode

6. • Parts in stock
• Mode
- The number or category that occurs the most
3 7 6 6 8
10 5 5 11 8
9 12 9 6 4
6 7 4 2 4
8 5 6 10 9
7 8 10 7 5
2 5 1 9 7
11 7 8 7 9
6 8 3 4 3
part number frequency
7 7
6 6
8 6
5 5
9 5
4 4
3 3
10 3
2 2
11 2
1 1
12 1
total 45

7. ◦ Data which can be ranked
 Count and put in order but not measure nor
ratio
◦ Examples
 Employee grades (A, B, C …)
 Voting preferences (best candidate, 2nd best
…)
 Product preferences
◦ Summary statistics
 Mode, median

8. • Score on rating scale
• Median
- Value of middle item of ordered data, (N +1)/2 term
score frequency
cumulative
frequency
1 1 1
2 2 3
3 3 6
4 4 10
5 5 15
6 6 21
7 7 28
8 6 34
9 5 39
10 3 42
11 2 44
12 1 45
3 7 6 6 8
10 5 5 11 8
9 12 9 6 4
6 7 4 2 4
8 5 6 10 9
7 8 10 7 5
2 5 1 9 7
11 7 8 7 9
6 8 3 4 3

9. ◦ Data which can be placed along a scale
 Count, put in order, measure but not ratio
◦ Examples
 Centigrade temperature scale (10C, 15C,
20C)
 IQ score (100, 115, 130)
◦ Summary statistics
 Mode, median, mean
 Range, standard deviation

10. • Temperature C
• Mean
- total value of all data / number of data
3 7 6 6 8
10 5 5 11 8
9 12 9 6 4
6 7 4 2 4
8 5 6 10 9
7 8 10 7 5
2 5 1 9 7
11 7 8 7 9
6 8 3 4 3
temperature
(x) Frequency (f) fx
1 1 1
2 2 4
3 3 9
4 4 16
5 5 25
6 6 36
7 7 49
8 6 48
9 5 45
10 3 30
11 2 22
12 1 12
total 45 297
 = mean = 297/45 = 6.6C

11.  Population variance is 𝜎2 =
𝑓 𝑖 𝑥 𝑖−𝜇 2
𝑁
 where𝑁 = 𝑓𝑖and the mean 𝜇 =
𝑓 𝑖 𝑥 𝑖
𝑁
 and the standard deviation is
 𝜎 =
𝑓𝑖 𝑥 𝑖−𝜇 2
𝑁

12. temperature
(x)
frequency
(f) fx x - m (x - m)2 f(x - m) 2
1 1 1 -5.6 31.36 31.36
2 2 4 -4.6 21.16 42.32
3 3 9 -3.6 12.96 38.88
4 4 16 -2.6 6.76 27.04
5 5 25 -1.6 2.56 12.80
6 6 36 -0.6 0.36 2.16
7 7 49 0.4 0.16 1.12
8 6 48 1.4 1.96 11.76
9 5 45 2.4 5.76 28.80
10 3 30 3.4 11.56 34.68
11 2 22 4.4 19.36 38.72
12 1 12 5.4 29.16 29.16
total 45 297 298.8

13.  𝑁 = 𝑓𝑖 = 45
 𝜇 =
𝑓 𝑖 𝑥 𝑖
𝑁
=
297
45
= 6.6
 𝜎 =
𝑓𝑖 𝑥 𝑖−𝜇 2
𝑁
=
298.8
45
= 2.577

14. ◦ Data along a scale which can be ratioed
 Count, put in order, measure and ratio
◦ Examples
 Kelvin temperature scale
 Time spent in queue (10, 20, 30 minutes)
 Differences on interval scales
◦ Summary statistics
 Mode, median, mean
 Range, standard deviation, coefficient of
variation, skewness

15. queuing time
(x)
frequency
(f) fx x - m
(x -
m)2 f(x - m) 2
1 1 1 -5.6 31.36 31.36
2 2 4 -4.6 21.16 42.32
etc. etc. etc. etc. etc. etc.
11 2 22 4.4 19.36 38.72
12 1 12 5.4 29.16 29.16
total 45 297 298.8
𝜇 =
𝑓𝑖 𝑥𝑖
𝑁
= 6.6𝜎 =
𝑓𝑖 𝑥𝑖 − 𝜇 2
𝑁
= 2.577
coefficient of variation 𝐶𝑉 =
𝜎
𝜇
=
2.577
6.6
= 0.39

16. ◦ Discrete data
 Can take a countable number of values
 Number of products built (1,237,502)
 Number of questions correct in test (4)
◦ Continuous
 Can take an uncountable number of values
 Length of fabric cut (45.9847248738…metres)
 Time in queue (23 minutes
5.2084792…seconds)

17. ◦ How to show the change of data (often price or
quantity) over time
 Relative to a reference point (the base period)
◦ e.g. simple price index (aka price relative)
𝑅 =
𝑝 𝑛
𝑝0
× 100where 0 denotes the base year
i.e. arbitrarily set price as 100 in base year

18. Consider chocolate bar, set 2009 as base year
Price (GBP)
Jan 2009 Jan 2010 Jan 2011
Chocolate bar 0.47 0.52 0.56
Sandwich 1.85 1.92 2.00
Bag of crisps 0.60 0.61 0.63
year price
Jan 2009 0.47 1.0000 100.00
Jan 2010 0.52 1.1064 110.64
Jan 2011 0.56 1.1915 119.15

19. ◦ Compare the prices of snack products over time
year chocolate bar
price index
sandwich
price index
bag of crisps
price index
Jan 2009 0.47 100.00 1.85 0.60
Jan 2010 0.52 110.64 1.92 0.61
Jan 2011 0.56 119.15 2.00 0.63
𝑅 =
𝑝 𝑛
𝑝0
× 100

20. year chocolate bar
price index
sandwich
price index
bag of crisps
price index
Jan 2009 0.47 100.00 1.85 100.00 0.60 100.00
Jan 2010 0.52 110.64 1.92 103.78 0.61 101.67
Jan 2011 0.56 119.15 2.00 108.11 0.63 105.00
95.00
100.00
105.00
110.00
115.00
120.00
125.00
priceindex£-
£0.50
£1.00
£1.50
£2.00
£2.50
priceperunit

21. % 𝑐ℎ𝑎𝑛𝑔𝑒 =
𝑛𝑒𝑤 𝑖𝑛𝑑𝑒𝑥 − 𝑜𝑙𝑑 𝑖𝑛𝑑𝑒𝑥
𝑜𝑙𝑑 𝑖𝑛𝑑𝑒𝑥
× 100
% 𝑐ℎ𝑎𝑛𝑔𝑒 =
119.15 − 110.64
110.64
× 100 = 7.69%
year chocolate bar
index annual
%
sandwich
price index
bag of crisps
price index
Jan
2009
100.00 - 100.00 - 100.00 -
Jan
2010
110.64 10.64 103.78 ? 101.67 ?
Jan
2011
119.15 7.69 108.11 ? 105.00 ?
year chocolate bar
index annual
%
sandwich
price index
bag of crisps
price index
Jan
2009
100.00 - 100.00 - 100.00 -
Jan
2010
110.64 10.64 103.78 3.78 101.67 1.67
Jan
2011
119.15 7.69 108.11 4.17 105.00 3.27

22. ◦ Reasons for changing base period;
 Mature series => large indices, relevance of base
period
 Compare different indices which have used different
base years
‘00 ‘01 ‘02 ‘03 ‘04 ‘05 ‘06 ‘07 ‘08 ‘09 ‘10 ‘11
Index
(‘02 as
base) 93 97 100 106 119 122 133 148 164 177 188 196
Index
(‘07 as
base) ? 100

23. ‘00 ‘01 ‘02 ‘03 ‘04 ‘05 ‘06 ‘07 ‘08 ‘09 ‘10 ‘11
Index
(‘02 as
base) 93 97 100 106 119 122 133 148 164 177 188 196
Index
(‘07 as
base) ? ? 68 ? ? ? ? 100 ? ? ? ?
‘00 ‘01 ‘02 ‘03 ‘04 ‘05 ‘06 ‘07 ‘08 ‘09 ‘10 ‘11
Index
(‘02 as
base) 93 97 100 106 119 122 133 148 164 177 188 196
Index
(‘07 as
base) 63 66 68 72 80 82 90 100 111 120 127 132

24. year price
chocolate bar sandwich bag of crisps I
Jan 2009 0.47 1.85 0.60 100.00
Jan 2010 0.52 1.92 0.61 104.45
Jan 2011 0.56 2.00 0.63 ?

26. 𝐿𝑃𝐼09 = 100 ×
𝑞09 𝑝09
𝑞09 𝑝09
= 100 ×
45 × 0.47 + 17 × 1.85 + 13 × 0.60
45 × 0.47 + 17 × 1.85 + 13 × 0.60
= 100
𝐿𝑃𝐼10 = 100 ×
𝑞09 𝑝10
𝑞09 𝑝09
= 100 ×
45 × 0.52 + 17 × 1.92 + 13 × 0.61
45 × 0.47 + 17 × 1.85 + 13 × 0.60
= 105.91
𝐿𝑃𝐼11 = 100 ×
𝑞09 𝑝11
𝑞09 𝑝09
= 100 ×
45 ×? + 17 ×? + 13 ×?
45 × 0.47 + 17 × 1.85 + 13 × 0.60
=? ? ?
year chocolate bar
price quantity
sandwich
price quantity
bag of crisps
price quantity
’09 0.47 45 1.85 17 0.60 13
’10 0.52 30 1.92 20 0.61 13
‘11 0.56 22 2.00 22 0.63 13

28. 𝑃𝑃𝐼09 = 100 ×
𝑞09 𝑝09
𝑞09 𝑝09
= 100 ×
45 × 0.47 + 17 × 1.85 + 13 × 0.60
45 × 0.47 + 17 × 1.85 + 13 × 0.60
= 100
𝑃𝑃𝐼10 = 100 ×
𝑞10 𝑝10
𝑞10 𝑝09
= 100 ×
30 × 0.52 + 20 × 1.92 + 13 × 0.61
30 × 0.47 + 20 × 1.85 + 13 × 0.60
= 105.14
𝑃𝑃𝐼11 = 100 ×
𝑞11 𝑝11
𝑞11 𝑝09
= 100 ×
?×? + ?×? + ?×?
?× 0.47 + ?× 1.85 + ?× 0.60
=? ? ?
year chocolate bar
price quantity
sandwich
price quantity
bag of crisps
price quantity
’09 0.47 45 1.85 17 0.60 13
’10 0.52 30 1.92 20 0.61 13
‘11 0.56 22 2.00 22 0.63 13

29. ◦ Weighted index number is defined as
𝑤𝑅
𝑤
◦ where w is the weight and Ris the price relative for
an item.
◦ e.g. weights represent fraction of total expenditure
on each item

30. ◦ Weighted index number is defined as
𝑤𝑅
𝑤
=
27358
100
= 273.58
w R
eggs 18 151.00 2718.00
flour 16 225.70 3611.20
fat 5 94.60 473.00
sugar 14 405.00 5670.00
lemons 2 256.40 512.80
gas 45 319.40 14373.00
100 27358.00

31. ◦ Use ratio of price indices to deflate actual values into
those of comparison year.
◦
104.7
108.5
× £17,127 = £16,527
1. ONS (2011)
Year CPI1 actual pay deflated (2007)
2007 104.7 £16,769 £16,769
2008 108.5 £17,127
2009 110.8 £17,582
2010 114.5 £17,940

32. Year CPI actual pay deflated (2007)
2007 104.7 £16,769 £16,769
2008 108.5 £17,127 £16,527
2009 110.8 £17,582 £16,614
2010 114.5 £17,940 £16,405
£16,000
£16,500
£17,000
£17,500
£18,000
actual
deflated (2007)

33. ◦ Recognise nominal, ordinal, interval and ratio data
types
◦ Recognise and use mode, median, mean, range,
standard deviation and coefficient of variation
◦ Calculate Laspeyres and Paasche index numbers
◦ Use index numbers to calculate percentage changes
and to deflate series

34. ◦ ONS (2011),
www.statistics.gov.uk/statbase/product.asp?vlnk=8
68, accessed 2nd March 2011

35. Any Questions?