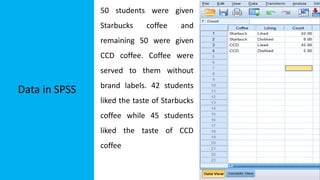
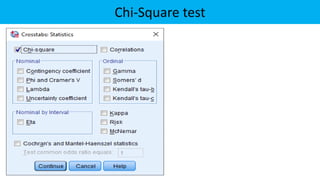
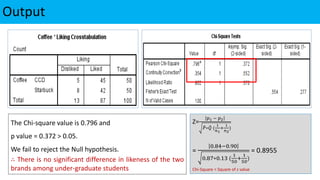
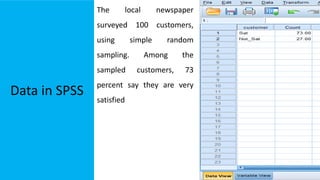
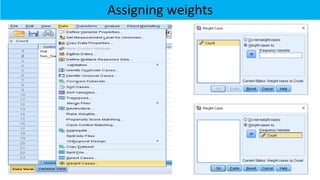
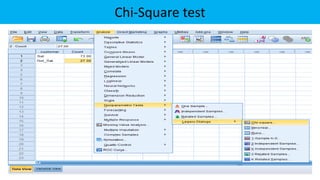
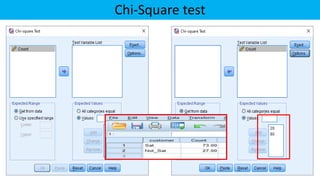
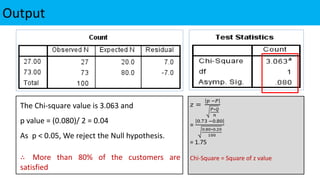
The document explains statistical tests for proportions using SPSS, detailing the test for a single proportion and the test for the difference between two proportions, including hypothesis formulation and statistical calculations. It includes case studies involving customer satisfaction and coffee brand preference, demonstrating how to apply the chi-square test and z-test in practical scenarios. The results indicate that the CEO's claim about customer satisfaction is supported, while there is no significant difference in preferences between the two coffee brands among undergraduate students.

1. TEST FOR PROPORTION(S)
USING SPSS

2. TEST FOR PROPORTION(S)
There are mainly two tests for proportion
• Test for single proportion
• Test for significant difference between proportion of two samples
SPSS does not have Z test to test the proportion(s).
But Chi-Square test can be used to the test the proportion in SPSS.

3. Chi- Square Statistic
If X~𝑁(𝜇, 𝜎2) then 𝑍 =
𝑋−𝜇
𝜎
~𝑁(0,1) and
𝑍2
=
𝑋−𝜇
𝜎
2
~𝜒2
with 1 d.f. and
𝑋−𝜇
𝜎
2
~𝜒2
with n d.f.

4. Test of Single
Proportion
Step 1: Null hypothesis H0: 𝑃 = 𝑃0
Step 2: Alternative hypothesis H1: 𝑃 ≠ 𝑃0 or 𝑃 > 𝑃0 or 𝑃 < 𝑃0
Step 3: Test statistics
𝑧 =
𝑝 −𝑃0
𝑃0 ∗𝑄0
𝑛
Denominator is the Standard Error of sample proportion i.e. S.E.(𝑝)
Step 4: Table value of z at 𝛼 % level of significance
Step 5: If z ≤ z table value, H0 is Accepted
If z > z table value, H0 is Rejected

5. Test of Single
Proportion
Step 1: Null hypothesis H0: 𝑃 = 𝑃0
Step 2: Alternative hypothesis H1: 𝑃 ≠ 𝑃0 or 𝑃 > 𝑃0 or 𝑃 < 𝑃0
Step 3: Check Assumptions
Step 4: Test statistic – Chi-square and p value
Step 5: Conclusion
• If p ≤ Level of significance (∝), We Reject Null hypothesis
• If p > Level of significance (∝), We fail to Reject Null hypothesis

6. Case Study
The CEO of a large water pump manufacturing company claims that more than 80 percent of
his customers are satisfied with the water pump. To test this claim, the local newspaper
surveyed 100 customers, using simple random sampling. Among the sampled customers, 73
percent say they are very satisfied. Based on these findings, what can we say about the
manufacturer’s claim ? Use a 0.05 level of significance.

7. Null & Alternative
Hypothesis
Step 1: H0: P = 0.80
[Not more than 80% of the customers are satisfied ]
Step 2: H1: P > 0.80
[More than 80% of the customers are satisfied ]
(One-tailed test)

8. Data in SPSS
The local newspaper
surveyed 100 customers,
using simple random
sampling. Among the
sampled customers, 73
percent say they are very
satisfied

9. Assigning weights

10. Chi-Square test

11. Chi-Square test

12. Output
The Chi-square value is 3.063 and
p value = (0.080)/ 2 = 0.04
As p < 0.05, We reject the Null hypothesis.
∴ More than 80% of the customers are
satisfied
𝑧 =
𝑝 −𝑃
𝑃∗𝑄
𝑛
=
0.73 −0.80
0.80∗0.20
100
= 1.75
Chi-Square = Square of z value

13. Test of significance of difference between two proportions
Step 1: Null hypothesis H0: 𝑃1= 𝑃2
Step 2: Alternative hypothesis H1: 𝑃1 ≠ 𝑃2 or 𝑃1 > 𝑃2 or 𝑃1 < 𝑃2
Step 3: Test statistics
𝑧 =
𝑝1 − 𝑝2
𝑃1∗𝑄1
𝑛1
+
𝑃2∗𝑄2
𝑛2
or
𝑝1 − 𝑝2
𝑃∗𝑄 (
1
𝑛1
+
1
𝑛2
)
where 𝑃 =
𝑛1𝑝1+𝑛2𝑝2
𝑛1+𝑛2
Denominator is the Standard Error of difference in sample proportion i.e. S.E.(𝑝1 − 𝑝2)
Step 4: Table value of z at 𝛼 % level of significance
Step 5: If z ≤ z table value, H0 is Accepted
If z > z table value, H0 is Rejected

14. Z test
for
two proportions
Step 1: Null hypothesis H0: 𝑃1 = 𝑃2
Step 2: Alternative hypothesis H1: 𝑃1≠ 𝑃2 or 𝑃1 > 𝑃2 or 𝑃1 < 𝑃2
Step 3: Check Assumptions
Step 4: Test statistic – Chi-square and p value
Step 5: Conclusion
• If p ≤ Level of significance (∝), We Reject Null hypothesis
• If p > Level of significance (∝), We fail to Reject Null hypothesis
Assumptions Tests
𝑛1 × 𝑝1 > 10 and 𝑛1 × (1 − 𝑝1) > 10
𝑛2 × 𝑝2 > 10 and 𝑛2 × (1 − 𝑝2) > 10
____

15. Case Study
Two brands of coffee - Starbucks and CCD were to be compared. A sample of 100 under-
graduate students were selected and of them randomly 50 students were given Starbucks
coffee and remaining 50 were given CCD coffee. Coffee were served to them without brand
labels. 42 students liked the taste of Starbucks coffee while 45 students liked the taste of CCD
coffee. Is there a significant difference in likeness of the two brands for the under-graduate
students?

16. Null & Alternative
Hypothesis
Step 1: H0: 𝑃1 = 𝑃1
[There is no significant difference in likeness of the two brands]
Step 2: H1: 𝑃1 ≠ 𝑃1
[There is significant difference in likeness of the two brands]
(Two-tailed test)

17. Data in SPSS
50 students were given
Starbucks coffee and
remaining 50 were given
CCD coffee. Coffee were
served to them without
brand labels. 42 students
liked the taste of Starbucks
coffee while 45 students
liked the taste of CCD
coffee

18. Assigning weights

19. Chi-Square test

20. Chi-Square test

21. Chi-Square test

22. Output
The Chi-square value is 0.796 and
p value = 0.372 > 0.05.
We fail to reject the Null hypothesis.
∴ There is no significant difference in likeness of the two
brands among under-graduate students
Z=
𝑝1 − 𝑝2
𝑃∗𝑄 (
1
𝑛1
+
1
𝑛2
)
=
0.84−0.90
0.87∗0.13 (
1
50
+
1
50
)
= 0.8955
Chi-Square = Square of z value

23. THANK YOU
Dr Parag Shah | M.Sc., M.Phil., Ph.D. ( Statistics)
pbshah@hlcollege.edu
www.paragstatistics.wordpress.com