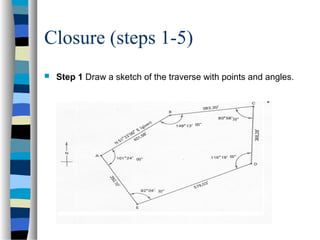
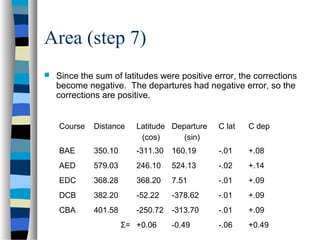
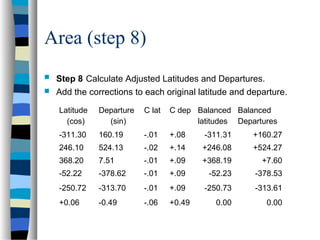
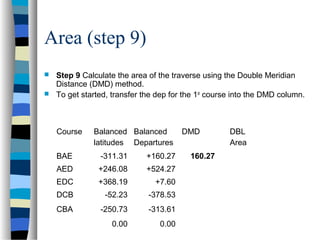
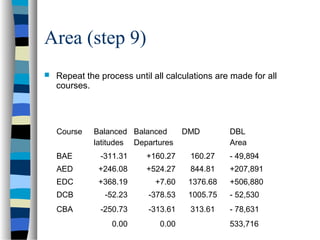
This document outlines the steps to compute the closure, accuracy, and area of a traverse survey. It discusses key terms, sources of error, and a 9-step process to calculate closure, precision ratio, and area using the double meridian distance method. As an example, it works through the calculations for a 5-sided closed traverse, determining the closure is 0.49 feet, precision ratio is 1:4200, and total area is 6.126 acres.

1. CMgt2340 Surveying
Chapter 6 Traverse
Surveys

2. Objectives




Match terms related to traversing with the
correct definitions.
List major sources of error in traverse
operations.
Perform traverse calculations in order to
determine closure, accuracy, and area.
Perform a closed loop traverse.

3. Terms and Definitions
 Angular
Error
 Closed Traverse
 Departure
 Error of Closure
 Latitude
 Open Traverse

4. Sources of Error in Traverse Operations



Errors in measurement of angles and
distances.
Poor selection of traverse points resulting in
bad sighting conditions (into sun, through
timber, etc.)
Failing to measure the angles an equal
number of times direct and reversed
(doubling and averaging)

5. 9 Steps to Computing a Traverse’s
Closure, Accuracy, and Area









1. Draw a sketch of the traverse with points and angles.
2. Compute the angular error and adjust the angles.
3. Compute the bearings or azimuths.
4. Compute Latitudes and Departures.
5. Compute the error of closure.
6. Compute the measure of accuracy.
7. Compute corrections for latitudes and departures.
8. Calculate Adjusted Latitudes and Departures.
9. Calculate the area of the traverse using the Double Meridian
Distance (DMD) method.

6. Problem (see figure 6.4 in text)


A five-sided closed field traverse has the
following angles: A=101°24’00”,
B=149°13’00”, C=80°58’30”, D=116° 19’00”,
E=92°04’30”. The lengths of the sides are as
follows: AE 350.10’, ED 579.03’, DC 368.28’,
CB 382.20’, BA 401.58’.
Determine the traverse’s closure, accuracy,
and area.

7. Closure (steps 1-5)

Step 1 Draw a sketch of the traverse with points and angles.
30”
00”
00”
00”
30”

8. Closure (steps 1-5)


Step 2 Compute the angular error and adjust the angles.
(n-2)180= (5-2)180= 540°00’00”
BAE
101°24’00”
+12”
101°24’12”
CBA
149°13’00”
+12”
149°13’12”
DCB
80°58’30”
+12”
80°58’42”
EDC
116°19’00”
+12”
116°19’12”
AED
92°04’30”
+12”
92°04’42”
539°59’00”
+12”
540°00’00”
Σ
-1’00”/5=-12”

9. Closure (steps 1-5)

Step 3 Compute the azimuths (or bearings).
Course
Azimuth
Bearing
BAE
152°46’12”
S27°13’48”E
AED
64°50’54”
N64°50’54”E
EDC
1°10’06”
N1°10’06”E
DCB
262°08’48”
S82°08’48”W
CBA
231°22’00”
S51°22’00”W

10. Closure (steps 1-5)






Step 4 Compute Latitudes and Departures.
What are latitudes and departures?
For any given line BA, latitude is the change in y and departure
is the change in x (see figure 6.6, p.167).
Latitude (north is +, south is -).
Departure (west is -, east is +).
If a survey has been perfectly performed, the plus latitudes will
equal the minus latitudes and the same with the departures.
Dep. BA (-)
Lat. BA (-)
A
B

11. Closure (steps 1-5)

Step 4 Compute Latitudes and Departures.

Formula for finding Lats and Deps
Latitude=Horizontal distance (H) cos θ
Departure=Horizontal distance (H) sin θ



12. Closure (steps 1-5)
On the TI-30xa calculator, enter 152.4612, 2nd key,
DMS-DD, cos, X, 350.10

Step 4 continued
STA
Distance
Azimuth
Latitude
(cos)
Departure
(sin)
BAE
350.10
152°46’12”
-311.30
160.19
AED
579.03
64°50’54”
246.10
524.13
EDC
368.28
1°10’06”
368.20
7.51
DCB
382.20
262°08’48”
-52.22
-378.62
CBA
401.58
231°22’00”
-250.72
-313.70

13. Closure (steps 1-5)
Step 5 Compute the error of closure (E).
 Sum the latitudes and departures. Since they do not equal zero, the
traverse did not make it back to the original point.
 The mathematical distance between the original point and the new point
is the error of closure (E) (see Fig. 6.11, p 156).
 E=square root of (Σlat2+Σdep2)=sq rt (0.062+0.492)=0.49

Course
Distance
Azimuth
Latitude Departure
(cos)
(sin)
BAE
350.10
152°46’12”
-311.30
160.19
AED
579.03
64°50’54”
246.10
524.13
EDC
368.28
1°10’06”
368.20
7.51
DCB
382.20
262°08’48”
-52.22
-378.62
CBA
401.58
231°22’00”
-250.72
-313.70
P= 2081.19
Σ= +0.06
-0.49

14. Accuracy (step 6)






Step 6 Compute the measure of accuracy.
Precision Ratio= Error of Closure (E) to Total distance around
the traverse (P).
Precision Ratio= E/P = 0.49/2081.19
Precision Ratios are always written with the numerator as 1,
thus if we divide both by the original numerator we have the new
format (1/4247)
We then round the denominator to the nearest 100.
= 1/4200

15. Accuracy (step 6)




What is the importance of the Precision Ratio?
So that states and provinces are able to mandate the
level of competency on given works.
A gravel road could pass with a 1/3000, whereas a
monorail would need a 1/7500 to 1/10000 level of
precision.
In our example, if we specified that the survey must
meet a 1/7500 Precision Ratio, we would have to
resurvey because we are only at 1/4200.

16. Area (step 7)




Step 7 Compute corrections for latitudes and departures.
Just like balancing angles, once we identify the sum of the
latitudes and departures, we need to distribute that error before
proceeding.
One way to distribute the error is through the compass rule.
This technique distributes errors in latitude and departure for
each course in the same proportion as the course distance is to
the traverse perimeter.

17. Area (step 7)







The formula is as follows:
C lat AB = Σ lat x AB/P
Where C lat AB = correction in latitude AB
Σ lat = error of closure in latitude
AB = distance AB
P = Perimeter of traverse
(the formula for departure is the same, just substitute
dep for lat)

18. Area (step 7)


Using the calculator, we can set up a
constant in memory such as .06/2081.19 and
then multiply this by each course distance.
For example, for the latitudes, perform the
above calculation and store it as M1. Then
for each course, enter RCL1, X, the next
course distance.

19. Area (step 7)

Since the sum of latitudes were positive error, the corrections
become negative. The departures had negative error, so the
corrections are positive.
Course
Distance
Latitude Departure
(cos)
(sin)
C lat
C dep
BAE
350.10
-311.30
160.19
-.01
+.08
AED
579.03
246.10
524.13
-.02
+.14
EDC
368.28
368.20
7.51
-.01
+.09
DCB
382.20
-52.22
-378.62
-.01
+.09
CBA
401.58
-250.72
-313.70
-.01
+.09
-0.49
-.06
+0.49
Σ= +0.06

20. Area (step 8)


Step 8 Calculate Adjusted Latitudes and Departures.
Add the corrections to each original latitude and departure.
Latitude
(cos)
Departure
(sin)
C lat
C dep Balanced Balanced
latitudes Departures
-311.30
160.19
-.01
+.08
-311.31
+160.27
246.10
524.13
-.02
+.14
+246.08
+524.27
368.20
7.51
-.01
+.09
+368.19
+7.60
-52.22
-378.62
-.01
+.09
-52.23
-378.53
-250.72
-313.70
-.01
+.09
-250.73
-313.61
+0.06
-0.49
-.06
+0.49
0.00
0.00

21. Area (step 9)
Step 9 Calculate the area of the traverse using the Double Meridian
Distance (DMD) method.
 To get started, transfer the dep for the 1st course into the DMD column.

Course
Balanced Balanced
latitudes Departures
BAE
-311.31
+160.27
AED
+246.08
+524.27
EDC
+368.19
+7.60
DCB
-52.23
-378.53
CBA
-250.73
-313.61
0.00
0.00
DMD
160.27
DBL
Area

22. Area (step 9)

Next, multiply the DMD of the 1st by lat of 1st and record in DBL
area for 1st.
X
Course
Balanced Balanced
latitudes Departures
BAE
-311.31
+160.27
AED
+246.08
+524.27
EDC
+368.19
+7.60
DCB
-52.23
-378.53
CBA
-250.73
-313.61
0.00
0.00
DMD
160.27
DBL
Area
= - 49,894

23. Area (step 9)

Add DMD of 1st row to dep of 1st row to dep of 2nd row and record in DMD
for 2nd row.
+
Course
Balanced Balanced
latitudes Departures
DMD
BAE
-311.31
+160.27
160.27
AED
+246.08
+524.27 = 844.81
EDC
+368.19
+7.60
DCB
-52.23
-378.53
CBA
-250.73
-313.61
0.00
0.00
DBL
Area
- 49,894

24. Area (step 9)

Repeat the steps (multiply the DMD of the 2nd by lat of 2nd and
record in DBL area for 2nd).
X
Course
Balanced Balanced
latitudes Departures
DMD
DBL
Area
BAE
-311.31
+160.27
160.27
- 49,894
AED
+246.08
+524.27
844.81
=+207,891
EDC
+368.19
+7.60
DCB
-52.23
-378.53
CBA
-250.73
-313.61
0.00
0.00

25. Area (step 9)

Repeat the process until all calculations are made for all
courses.
Course
Balanced Balanced
latitudes Departures
DMD
DBL
Area
BAE
-311.31
+160.27
160.27
- 49,894
AED
+246.08
+524.27
844.81
+207,891
EDC
+368.19
+7.60
1376.68
+506,880
DCB
-52.23
-378.53
1005.75
- 52,530
CBA
-250.73
-313.61
313.61
- 78,631
0.00
0.00
533,716

26. Area (step 9)




Sum all of DBL areas and divide by 2
533,716 sq ft /2=266,858 sq ft
Divide by 43,560 sq ft /acre to find answer in acres
266,858/43,560 = 6.126 acres

27. References Cited
 Examples
and step by step tutorials
were copied directly from the following:
 Mid-America Vocational Curriculum
Consortium, Inc., Basic Surveying
Technology, Stillwater, OK: Oklahoma
State Department of Vocational
Technical Education, 1987