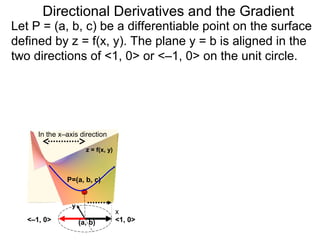
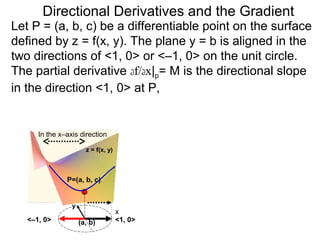
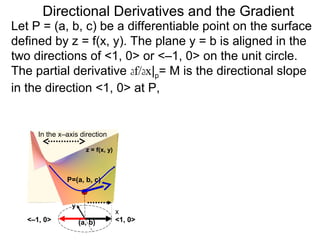
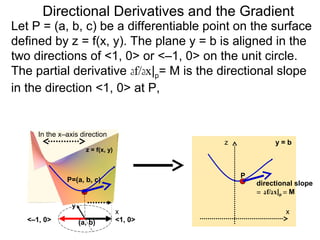
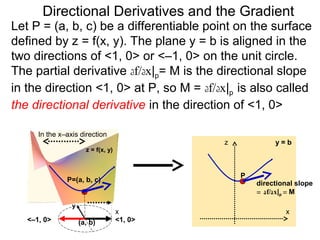
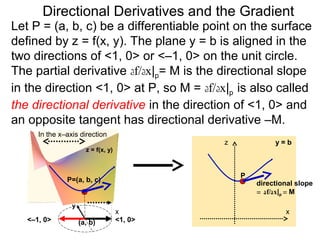
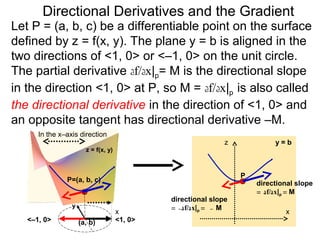
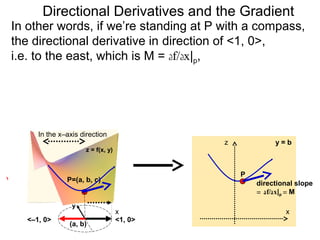
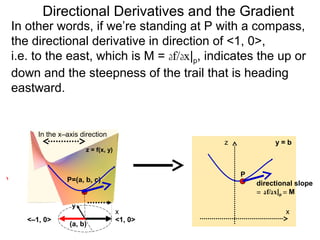
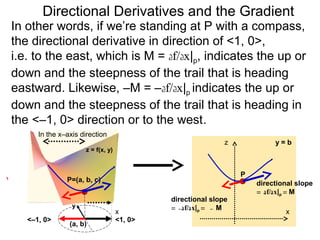
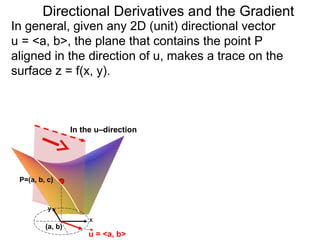
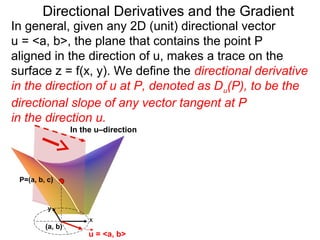
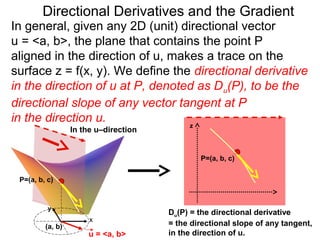
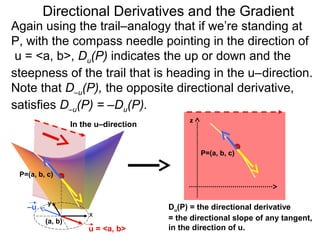
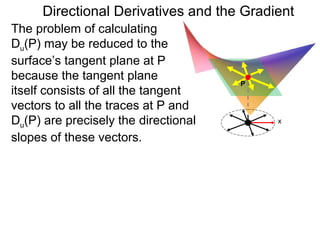
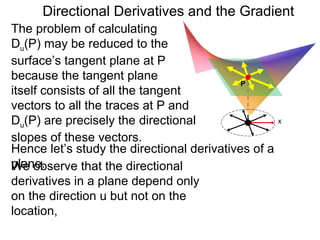
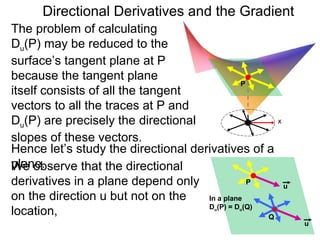
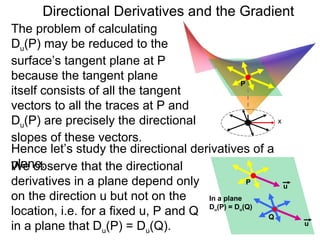
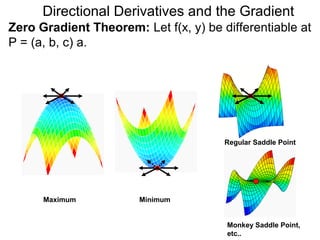
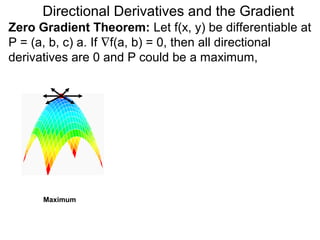
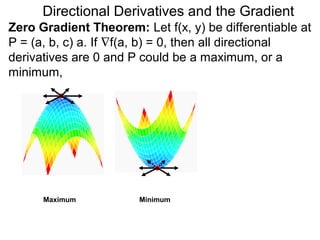
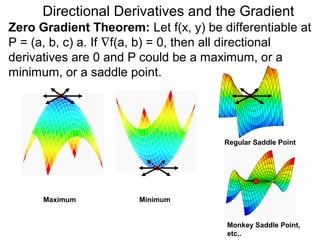
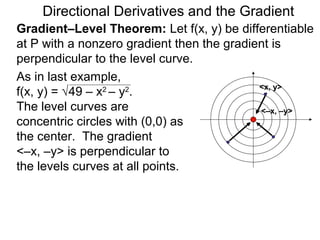
The document discusses directional derivatives and the gradient. It defines the directional slope of a vector v as the ratio of the y-component to the x-component of v. It then gives an example of calculating the directional slopes of several vectors. It explains that the directional slope indicates the steepness and direction of v. For a differentiable function f(x), the directional derivative in the direction of the unit vector <1,0> is the partial derivative df/dx, while the opposite direction has derivative -df/dx.

1. Directional Derivatives and the Gradient

2. Directional Derivatives and the Gradient
Given a vector v = <x, y>, we define the directional
y
slope of v to be
|x|.

3. Directional Derivatives and the Gradient
Given a vector v = <x, y>, we define the directional
y
slope of v to be
|x|.
Example A. Find the directional slope of
<1, 2>, <–1, –2>, <1, –2> and <–1, 2>.

4. Directional Derivatives and the Gradient
Given a vector v = <x, y>, we define the directional
y
slope of v to be
|x|.
Example A. Find the directional slope of
<1, 2>, <–1, –2>, <1, –2> and <–1, 2>.
The directional slope of y
<–1, 2> <1, 2>
a. <1, 2> is 2,
b. <–1, 2> is 2, x

5. Directional Derivatives and the Gradient
Given a vector v = <x, y>, we define the directional
y
slope of v to be
|x|.
Example A. Find the directional slope of
<1, 2>, <–1, –2>, <1, –2> and <–1, 2>.
The directional slope of y
<–1, 2> <1, 2>
a. <1, 2> is 2,
b. <–1, 2> is 2, x
c. <–1, –2> is –2, <–1, –2> <1, –2>
d. <1, –2> is –2.

6. Directional Derivatives and the Gradient
Given a vector v = <x, y>, we define the directional
y
slope of v to be
|x|.
Example A. Find the directional slope of
<1, 2>, <–1, –2>, <1, –2> and <–1, 2>.
The directional slope of y
<–1, 2> <1, 2>
a. <1, 2> is 2,
b. <–1, 2> is 2, x
c. <–1, –2> is –2, <–1, –2> <1, –2>
d. <1, –2> is –2.
The directional slope of v indicates the steepness of v
and the vertical direction it’s pointing.
Positive directional slope indicates v points upward and
negative directional slope means v points downward.

7. Directional Derivatives and the Gradient
y = f(x)
Given a differentiable point p on the
p
curve y = f(x) and a tangent vector v at p,
depending whether v points up or down,
we obtain two possible directional slopes for v.

8. Directional Derivatives and the Gradient
y = f(x)
Given a differentiable point p on the
p
curve y = f(x) and a tangent vector v at p,
depending whether v points up or down,
we obtain two possible directional slopes for v.
If v points to the right in the positive x–axis direction
then its directional slope is f '(x), and if v points to the
left then the directional slope of v is –f '(x).

9. Directional Derivatives and the Gradient
y = f(x)
Given a differentiable point p on the
p
curve y = f(x) and a tangent vector v at p,
depending whether v points up or down,
we obtain two possible directional slopes for v.
If v points to the right in the positive x–axis direction
then its directional slope is f '(x), and if v points to the
left then the directional slope of v is –f '(x).
For example, v = <1, –2> and u = <–2, 4> y=x 2
u = <–2, 4> are tangent to y = x 2
at (–1, 1),
x
v = <1, –2>

10. Directional Derivatives and the Gradient
y = f(x)
Given a differentiable point p on the
p
curve y = f(x) and a tangent vector v at p,
depending whether v points up or down,
we obtain two possible directional slopes for v.
If v points to the right in the positive x–axis direction
then its directional slope is f '(x), and if v points to the
left then the directional slope of v is –f '(x).
For example, v = <1, –2> and y=x 2
u = <–2, 4> are tangent to y = x 2
at (–1, 1), v points to the positive
x–axis direction, so its directional
slope is –2 = f '(x),
x
v = <1, –2>

11. Directional Derivatives and the Gradient
y = f(x)
Given a differentiable point p on the
p
curve y = f(x) and a tangent vector v at p,
depending whether v points up or down,
we obtain two possible directional slopes for v.
If v points to the right in the positive x–axis direction
then its directional slope is f '(x), and if v points to the
left then the directional slope of v is –f '(x).
For example, v = <1, –2> and u = <–2, 4> y=x 2
u = <–2, 4> are tangent to y = x 2
at (–1, 1), v points to the positive
x–axis direction, so its directional
slope is –2 = f '(x), and u points in
x
the negative x–axis direction with
directional slope 2 = –f '(x). v = <1, –2>

12. Directional Derivatives and the Gradient
Let P = (a, b, c) be a differentiable point on the surface
defined by z = f(x, y). The plane y = b is aligned in the
two directions of <1, 0> or <–1, 0> on the unit circle.

13. Directional Derivatives and the Gradient
Let P = (a, b, c) be a differentiable point on the surface
defined by z = f(x, y). The plane y = b is aligned in the
two directions of <1, 0> or <–1, 0> on the unit circle.
In the x–axis direction
z = f(x, y)
P=(a, b, c)
y
x
<–1, 0> (a, b) <1, 0>

14. Directional Derivatives and the Gradient
Let P = (a, b, c) be a differentiable point on the surface
defined by z = f(x, y). The plane y = b is aligned in the
two directions of <1, 0> or <–1, 0> on the unit circle.
The partial derivative df/dx|p= M is the directional slope
in the direction <1, 0> at P,
In the x–axis direction
z = f(x, y)
P=(a, b, c)
y
x
<–1, 0> (a, b) <1, 0>

15. Directional Derivatives and the Gradient
Let P = (a, b, c) be a differentiable point on the surface
defined by z = f(x, y). The plane y = b is aligned in the
two directions of <1, 0> or <–1, 0> on the unit circle.
The partial derivative df/dx|p= M is the directional slope
in the direction <1, 0> at P,
In the x–axis direction
z = f(x, y)
P=(a, b, c)
y
x
<–1, 0> (a, b) <1, 0>

16. Directional Derivatives and the Gradient
Let P = (a, b, c) be a differentiable point on the surface
defined by z = f(x, y). The plane y = b is aligned in the
two directions of <1, 0> or <–1, 0> on the unit circle.
The partial derivative df/dx|p= M is the directional slope
in the direction <1, 0> at P,
In the x–axis direction
z y=b
z = f(x, y)
P
P=(a, b, c)
directional slope
= df/dx|p = M
y
x x
<–1, 0> (a, b) <1, 0>

17. Directional Derivatives and the Gradient
Let P = (a, b, c) be a differentiable point on the surface
defined by z = f(x, y). The plane y = b is aligned in the
two directions of <1, 0> or <–1, 0> on the unit circle.
The partial derivative df/dx|p= M is the directional slope
in the direction <1, 0> at P, so M = df/dx|p is also called
the directional derivative in the direction of <1, 0>
In the x–axis direction
z y=b
z = f(x, y)
P
P=(a, b, c)
directional slope
= df/dx|p = M
y
x x
<–1, 0> (a, b) <1, 0>

18. Directional Derivatives and the Gradient
Let P = (a, b, c) be a differentiable point on the surface
defined by z = f(x, y). The plane y = b is aligned in the
two directions of <1, 0> or <–1, 0> on the unit circle.
The partial derivative df/dx|p= M is the directional slope
in the direction <1, 0> at P, so M = df/dx|p is also called
the directional derivative in the direction of <1, 0> and
an opposite tangent has directional derivative –M.
In the x–axis direction
z y=b
z = f(x, y)
P
P=(a, b, c)
directional slope
= df/dx|p = M
y
x x
<–1, 0> (a, b) <1, 0>

19. Directional Derivatives and the Gradient
Let P = (a, b, c) be a differentiable point on the surface
defined by z = f(x, y). The plane y = b is aligned in the
two directions of <1, 0> or <–1, 0> on the unit circle.
The partial derivative df/dx|p= M is the directional slope
in the direction <1, 0> at P, so M = df/dx|p is also called
the directional derivative in the direction of <1, 0> and
an opposite tangent has directional derivative –M.
In the x–axis direction
z y=b
z = f(x, y)
P
P=(a, b, c)
directional slope
= df/dx|p = M
directional slope
y = –df/dx|p = – M
x x
<–1, 0> (a, b) <1, 0>

20. Directional Derivatives and the Gradient
In other words, if we’re standing at P with a compass,
the directional derivative in direction of <1, 0>,
i.e. to the east, which is M = df/dx|p,
In the x–axis direction
z y=b
z = f(x, y)
P
P=(a, b, c)
directional slope
= df/dx|p = M
y
x x
<–1, 0> <1, 0>
(a, b)

21. Directional Derivatives and the Gradient
In other words, if we’re standing at P with a compass,
the directional derivative in direction of <1, 0>,
i.e. to the east, which is M = df/dx|p, indicates the up or
down and the steepness of the trail that is heading
eastward.
In the x–axis direction
z y=b
z = f(x, y)
P
P=(a, b, c)
directional slope
= df/dx|p = M
y
x x
<–1, 0> <1, 0>
(a, b)

22. Directional Derivatives and the Gradient
In other words, if we’re standing at P with a compass,
the directional derivative in direction of <1, 0>,
i.e. to the east, which is M = df/dx|p, indicates the up or
down and the steepness of the trail that is heading
eastward. Likewise, –M = –df/dx|p indicates the up or
down and the steepness of the trail that is heading in
the <–1, 0> direction or to the west.
In the x–axis direction
z y=b
z = f(x, y)
P
P=(a, b, c)
directional slope
= df/dx|p = M
directional slope
y = –df/dx|p = – M
x x
<–1, 0> <1, 0>
(a, b)

23. Directional Derivatives and the Gradient
In general, given any 2D (unit) directional vector
u = <a, b>,
y
x
(a, b)
u = <a, b>

24. Directional Derivatives and the Gradient
In general, given any 2D (unit) directional vector
u = <a, b>, the plane that contains the point P
aligned in the direction of u, makes a trace on the
surface z = f(x, y).
y
x
(a, b)
u = <a, b>

25. Directional Derivatives and the Gradient
In general, given any 2D (unit) directional vector
u = <a, b>, the plane that contains the point P
aligned in the direction of u, makes a trace on the
surface z = f(x, y).
In the u–direction
P=(a, b, c)
y
x
(a, b)
u = <a, b>

26. Directional Derivatives and the Gradient
In general, given any 2D (unit) directional vector
u = <a, b>, the plane that contains the point P
aligned in the direction of u, makes a trace on the
surface z = f(x, y). We define the directional derivative
in the direction of u at P, denoted as D u(P), to be the
directional slope of any vector tangent at P
in the direction u.
In the u–direction
P=(a, b, c)
y
x
(a, b)
u = <a, b>

27. Directional Derivatives and the Gradient
In general, given any 2D (unit) directional vector
u = <a, b>, the plane that contains the point P
aligned in the direction of u, makes a trace on the
surface z = f(x, y). We define the directional derivative
in the direction of u at P, denoted as D u(P), to be the
directional slope of any vector tangent at P
in the direction u. z
In the u–direction
P=(a, b, c)
P=(a, b, c)
y
Du(P) = the directional derivative
x
(a, b) = the directional slope of any tangent,
u = <a, b> in the direction of u.

28. Directional Derivatives and the Gradient
Again using the trail–analogy that if we’re standing at
P, with the compass needle pointing in the direction of
u = <a, b>, Du(P) indicates the up or down and the
steepness of the trail that is heading in the u–direction.
z
In the u–direction
P=(a, b, c)
P=(a, b, c)
y
Du(P) = the directional derivative
x
(a, b) = the directional slope of any tangent,
u = <a, b> in the direction of u.

29. Directional Derivatives and the Gradient
Again using the trail–analogy that if we’re standing at
P, with the compass needle pointing in the direction of
u = <a, b>, Du(P) indicates the up or down and the
steepness of the trail that is heading in the u–direction.
Note that D–u(P), the opposite directional derivative,
satisfies D–u(P) = –Du(P).
z
In the u–direction
P=(a, b, c)
P=(a, b, c)
y
–u Du(P) = the directional derivative
x
(a, b) = the directional slope of any tangent,
u = <a, b> in the direction of u.

30. Directional Derivatives and the Gradient
The problem of calculating
Du(P) may be reduced to the
surface’s tangent plane at P
because the tangent plane
itself consists of all the tangent
vectors to all the traces at P

31. Directional Derivatives and the Gradient
The problem of calculating
Du(P) may be reduced to the
surface’s tangent plane at P
because the tangent plane
P
itself consists of all the tangent
vectors to all the traces at P

32. Directional Derivatives and the Gradient
The problem of calculating
Du(P) may be reduced to the
surface’s tangent plane at P
because the tangent plane
P
itself consists of all the tangent
vectors to all the traces at P and
Du(P) are precisely the directional x
slopes of these vectors.

33. Directional Derivatives and the Gradient
The problem of calculating
Du(P) may be reduced to the
surface’s tangent plane at P
because the tangent plane
P
itself consists of all the tangent
vectors to all the traces at P and
Du(P) are precisely the directional x
slopes of these vectors.
Hence let’s study the directional derivatives of a
plane.

34. Directional Derivatives and the Gradient
The problem of calculating
Du(P) may be reduced to the
surface’s tangent plane at P
because the tangent plane
P
itself consists of all the tangent
vectors to all the traces at P and
Du(P) are precisely the directional x
slopes of these vectors.
Hence let’s study the directional derivatives of a
plane.
We observe that the directional
derivatives in a plane depend only
on the direction u but not on the
location,

35. Directional Derivatives and the Gradient
The problem of calculating
Du(P) may be reduced to the
surface’s tangent plane at P
because the tangent plane
P
itself consists of all the tangent
vectors to all the traces at P and
Du(P) are precisely the directional x
slopes of these vectors.
Hence let’s study the directional derivatives of a
plane.
We observe that the directional
derivatives in a plane depend only P
u
on the direction u but not on the In a plane
D (P) = D (Q)
location, u u
Q
u

36. Directional Derivatives and the Gradient
The problem of calculating
Du(P) may be reduced to the
surface’s tangent plane at P
because the tangent plane
P
itself consists of all the tangent
vectors to all the traces at P and
Du(P) are precisely the directional x
slopes of these vectors.
Hence let’s study the directional derivatives of a
plane.
We observe that the directional
derivatives in a plane depend only P
u
on the direction u but not on the In a plane
location, i.e. for a fixed u, P and Q D (P) = D (Q) Q
u u
in a plane that Du(P) = Du(Q). u

37. Directional Derivatives and the Gradient
We also note that the directional derivatives in the
plane are determined by the way the plane sits in
space. For example, a flat plane defined by z = c has
the Du(P) = 0 for all u's and P's.

38. Directional Derivatives and the Gradient
We also note that the directional derivatives in the
plane are determined by the way the plane sits in
space. For example, a flat plane defined by z = c has
the Du(P) = 0 for all u's and P's. The direction that a
plane T faces is determined by its partials derivative
df/dx = M and df/dy = L. In particular
we may reconstruct the plane
using M and L as shown.

39. Directional Derivatives and the Gradient
We also note that the directional derivatives in the
plane are determined by the way the plane sits in
space. For example, a flat plane defined by z = c has
the Du(P) = 0 for all u's and P's. The direction that a
plane T faces is determined by its partials derivative
df/dx = M and df/dy = L. In particular
we may reconstruct the plane
using M and L as shown. Mdx
x
dx

40. Directional Derivatives and the Gradient
We also note that the directional derivatives in the
plane are determined by the way the plane sits in
space. For example, a flat plane defined by z = c has
the Du(P) = 0 for all u's and P's. The direction that a
plane T faces is determined by its partials derivative
df/dx = M and df/dy = L. In particular
we may reconstruct the plane
using M and L as shown. Ldy
Mdx
x
y
dy dx

41. Directional Derivatives and the Gradient
We also note that the directional derivatives in the
plane are determined by the way the plane sits in
space. For example, a flat plane defined by z = c has
the Du(P) = 0 for all u's and P's. The direction that a
plane T faces is determined by its partials derivative
df/dx = M and df/dy = L. In particular
we may reconstruct the plane
using M and L as shown. Ldy
Mdx
x
y
dy dx

42. Directional Derivatives and the Gradient
We also note that the directional derivatives in the
plane are determined by the way the plane sits in
space. For example, a flat plane defined by z = c has
the Du(P) = 0 for all u's and P's. The direction that a
plane T faces is determined by its partials derivative
df/dx = M and df/dy = L. In particular
we may reconstruct the plane
using M and L as shown. Ldy
Mdx
The Gradient y
x
The vector <M, L> is called the
dy dx
gradient (vector) of T.

43. Directional Derivatives and the Gradient
We also note that the directional derivatives in the
plane are determined by the way the plane sits in
space. For example, a flat plane defined by z = c has
the Du(P) = 0 for all u's and P's. The direction that a
plane T faces is determined by its partials derivative
df/dx = M and df/dy = L. In particular The gradient
∇ f(P) = <M,L>
we may reconstruct the plane
using M and L as shown. Ldy
Mdx
The Gradient y
<M,L> x
The vector <M, L> is called the M
dy dx
gradient (vector) of T. L

44. Directional Derivatives and the Gradient
We also note that the directional derivatives in the
plane are determined by the way the plane sits in
space. For example, a flat plane defined by z = c has
the Du(P) = 0 for all u's and P's. The direction that a
plane T faces is determined by its partials derivative
df/dx = M and df/dy = L. In particular The gradient
∇ f(P) = <M,L>
we may reconstruct the plane
using M and L as shown. Ldy
Mdx
The Gradient y
<M,L> x
The vector <M, L> is called the M
dy dx
gradient (vector) of T. L
If T is the tangent plane at P to the surface z = f(x, y),
then we call <M, L> the gradient at P,
and is denoted as∇ f(P), i.e. ∇ f(P) = (fx(P), fy(P)).

45. Directional Derivatives and the Gradient
Gradient–Directional Derivative Theorem: Given
that z = f(x, y) is differentiable at P, the directional
derivative at P in the direction of u = <a, b> with |u| = 1
is Duf(x, y) = ∇f(x, y) • u = <M, L> • <a, b> = Ma + Lb.

46. Directional Derivatives and the Gradient
Gradient–Directional Derivative Theorem: Given
that z = f(x, y) is differentiable at P, the directional
derivative at P in the direction of u = <a, b> with |u| = 1
is Duf(x, y) = ∇f(x, y) • u = <M, L> • <a, b> = Ma + Lb.
Example B. Let f(x, y) = √49 – x2 – y2 and P = (3, 2, 6).
Find the gradient at P, and the directional derivative
with u = < 4/5, 3/5>.

47. Directional Derivatives and the Gradient
Gradient–Directional Derivative Theorem: Given
that z = f(x, y) is differentiable at P, the directional
derivative at P in the direction of u = <a, b> with |u| = 1
is Duf(x, y) = ∇f(x, y) • u = <M, L> • <a, b> = Ma + Lb.
Example B. Let f(x, y) = √49 – x2 – y2 and P = (3, 2, 6).
Find the gradient at P, and the directional derivative
with u = < 4/5, 3/5>.
We need ∇f(3, 2) = (fx(3, 2), fy(3, 2)) where
fx = –x/√49 – x2 – y2, fy = –y/√49 – x2 – y2 .

48. Directional Derivatives and the Gradient
Gradient–Directional Derivative Theorem: Given
that z = f(x, y) is differentiable at P, the directional
derivative at P in the direction of u = <a, b> with |u| = 1
is Duf(x, y) = ∇f(x, y) • u = <M, L> • <a, b> = Ma + Lb.
Example B. Let f(x, y) = √49 – x2 – y2 and P = (3, 2, 6).
Find the gradient at P, and the directional derivative
with u = < 4/5, 3/5>.
We need ∇f(3, 2) = (fx(3, 2), fy(3, 2)) where
fx = –x/√49 – x2 – y2, fy = –y/√49 – x2 – y2 .
So M = –1/2 and L = –1/3 and the
gradient at P is ∇f(3, 2) = <–1/2, –1/3>.

49. Directional Derivatives and the Gradient
Gradient–Directional Derivative Theorem: Given
that z = f(x, y) is differentiable at P, the directional
derivative at P in the direction of u = <a, b> with |u| = 1
is Duf(x, y) = ∇f(x, y) • u = <M, L> • <a, b> = Ma + Lb.
Example B. Let f(x, y) = √49 – x2 – y2 and P = (3, 2, 6).
Find the gradient at P, and the directional derivative
with u = < 4/5, 3/5>.
We need ∇f(3, 2) = (fx(3, 2), fy(3, 2)) where
fx = –x/√49 – x2 – y2, fy = –y/√49 – x2 – y2 .
So M = –1/2 and L = –1/3 and the
gradient at P is ∇f(3, 2) = <–1/2, –1/3>.
The directional derivative Duf(2, 3)
with u = <4/5, –3/5> is ∇f(3, 2) • u

50. Directional Derivatives and the Gradient
Gradient–Directional Derivative Theorem: Given
that z = f(x, y) is differentiable at P, the directional
derivative at P in the direction of u = <a, b> with |u| = 1
is Duf(x, y) = ∇f(x, y) • u = <M, L> • <a, b> = Ma + Lb.
Example B. Let f(x, y) = √49 – x2 – y2 and P = (3, 2, 6).
Find the gradient at P, and the directional derivative
with u = < 4/5, 3/5>.
We need ∇f(3, 2) = (fx(3, 2), fy(3, 2)) where
fx = –x/√49 – x2 – y2, fy = –y/√49 – x2 – y2 .
So M = –1/2 and L = –1/3 and the
gradient at P is ∇f(3, 2) = <–1/2, –1/3>.
The directional derivative Duf(2, 3)
with u = <4/5, –3/5> is ∇f(3, 2) • u
= <–1/2, –1/3> • <4/5, –3/5> = –1/5.

51. Directional Derivatives and the Gradient
Gradient–Directional Derivative Theorem: Given
that z = f(x, y) is differentiable at P, the directional
derivative at P in the direction of u = <a, b> with |u| = 1
is Duf(x, y) = ∇f(x, y) • u = <M, L> • <a, b> = Ma + Lb.
Example B. Let f(x, y) = √49 – x2 – y2 and P = (3, 2, 6).
Find the gradient at P, and the directional derivative
with u = < 4/5, 3/5>.
We need ∇f(3, 2) = (fx(3, 2), fy(3, 2)) where
fx = –x/√49 – x2 – y2, fy = –y/√49 – x2 – y2 .
So M = –1/2 and L = –1/3 and the D f(2, 3)=–1/5
u
(3, 2, 6)
gradient at P is ∇f(3, 2) = <–1/2, –1/3>.
The directional derivative Duf(2, 3) y
with u = <4/5, –3/5> is ∇f(3, 2) • u x (3, 2, 0)
= <–1/2, –1/3> • <4/5, –3/5> = –1/5. u=<4/5, –3/5>

52. Directional Derivatives and the Gradient
Zero Gradient Theorem: Let f(x, y) be differentiable at
P = (a, b, c) a.
Regular Saddle Point
Maximum Minimum
Monkey Saddle Point,
etc..

53. Directional Derivatives and the Gradient
Zero Gradient Theorem: Let f(x, y) be differentiable at
P = (a, b, c) a. If ∇f(a, b) = 0, then all directional
derivatives are 0

54. Directional Derivatives and the Gradient
Zero Gradient Theorem: Let f(x, y) be differentiable at
P = (a, b, c) a. If ∇f(a, b) = 0, then all directional
derivatives are 0 and P could be a maximum,
Maximum

55. Directional Derivatives and the Gradient
Zero Gradient Theorem: Let f(x, y) be differentiable at
P = (a, b, c) a. If ∇f(a, b) = 0, then all directional
derivatives are 0 and P could be a maximum, or a
minimum,
Maximum Minimum

56. Directional Derivatives and the Gradient
Zero Gradient Theorem: Let f(x, y) be differentiable at
P = (a, b, c) a. If ∇f(a, b) = 0, then all directional
derivatives are 0 and P could be a maximum, or a
minimum, or a saddle point.
Regular Saddle Point
Maximum Minimum
Monkey Saddle Point,
etc..

57. Directional Derivatives and the Gradient
Gradient–Steepness Theorem: Let f(x, y) be
differentiable at P = (a, b, c) and ∇f(a, b) = <M, L>
(≠ 0) then <M, L> gives the direction of maximum
directional derivative (steepest climb) with value equal
to |<M, L>|. The opposite direction <–M, –L> gives the
direction of minimum directional derivative (steepest
descend) with value –|<M, L>|.

58. Directional Derivatives and the Gradient
Gradient–Steepness Theorem: Let f(x, y) be
differentiable at P = (a, b, c) and ∇f(a, b) = <M, L>
(≠ 0) then <M, L> gives the direction of maximum
directional derivative (steepest climb) with value equal
to |<M, L>|. The opposite direction <–M, –L> gives the
direction of minimum directional derivative (steepest
descend) with value –|<M, L>|.
The gradient
∇ f(P) = <M,L>
Mdx
Ldy
<M,L> x
y
M
dy dx
L

59. Directional Derivatives and the Gradient
Gradient–Steepness Theorem: Let f(x, y) be
differentiable at P = (a, b, c) and ∇f(a, b) = <M, L>
(≠ 0) then <M, L> gives the direction of maximum
directional derivative (steepest climb) with value equal
to |<M, L>|. The opposite direction <–M, –L> gives the
direction of minimum directional derivative (steepest
descend) with value –|<M, L>|. Here is an example of
the steepest direction in a plane.
The gradient The Steepest Climb (0, 1, 1/2)
∇ f(P) = <M,L>
Mdx
Ldy 1/2
<M,L> x (1, 0, 1/4)
y
M 1
1/4 y
dy dx 1
L <1/4, 1/2>=∇f
x The Steepest Direction

60. Directional Derivatives and the Gradient
Example: Let f(x, y) = √k – x2 – y2, with k > 0. Draw the
gradient in the R2 plane at (a, b) in the domain.

61. Directional Derivatives and the Gradient
Example: Let f(x, y) = √k – x2 – y2, with k > 0. Draw the
gradient in the R2 plane at (a, b) in the domain.
We have fx = –x/√49 – x2 – y2, fy = –y/√49 – x2 – y2 .

62. Directional Derivatives and the Gradient
Example: Let f(x, y) = √k – x2 – y2, with k > 0. Draw the
gradient in the R2 plane at (a, b) in the domain.
We have fx = –x/√49 – x2 – y2, fy = –y/√49 – x2 – y2 .
At (a, b) in the domain, after clearing the
denominator, we've the direction the gradient or the
direction of the steepest climb to be <–a, –b>.

63. Directional Derivatives and the Gradient
Example: Let f(x, y) = √k – x2 – y2, with k > 0. Draw the
gradient in the R2 plane at (a, b) in the domain.
We have fx = –x/√49 – x2 – y2, fy = –y/√49 – x2 – y2 .
At (a, b) in the domain, after clearing the
denominator, we've the direction the gradient or the
direction of the steepest climb to be <–a, –b>.
The surface is a hemisphere
centered at the origin hence
<–a, –b> is the direction to the
top which is also the direction of
the steepest climb.

64. Directional Derivatives and the Gradient
Example: Let f(x, y) = √k – x2 – y2, with k > 0. Draw the
gradient in the R2 plane at (a, b) in the domain.
We have fx = –x/√49 – x2 – y2, fy = –y/√49 – x2 – y2 .
At (a, b) in the domain, after clearing the
denominator, we've the direction the gradient or the
direction of the steepest climb to be <–a, –b>.
(a,b)
The surface is a hemisphere
centered at the origin hence
<–a, –b> is the direction to the <–a,–b>
top which is also the direction of
the steepest climb.

65. Directional Derivatives and the Gradient
Gradient–Level Theorem: Let f(x, y) be differentiable
at P with a nonzero gradient then the gradient is
perpendicular to the level curve.

66. Directional Derivatives and the Gradient
Gradient–Level Theorem: Let f(x, y) be differentiable
at P with a nonzero gradient then the gradient is
perpendicular to the level curve.
As in last example,
f(x, y) = √49 – x2 – y2.
The level curves are
concentric circles with (0,0) as
the center.

67. Directional Derivatives and the Gradient
Gradient–Level Theorem: Let f(x, y) be differentiable
at P with a nonzero gradient then the gradient is
perpendicular to the level curve.
As in last example,
<x, y>
f(x, y) = √49 – x2 – y2.
The level curves are <–x, –y>
concentric circles with (0,0) as
the center. The gradient
<–x, –y> is perpendicular to
the levels curves at all points.