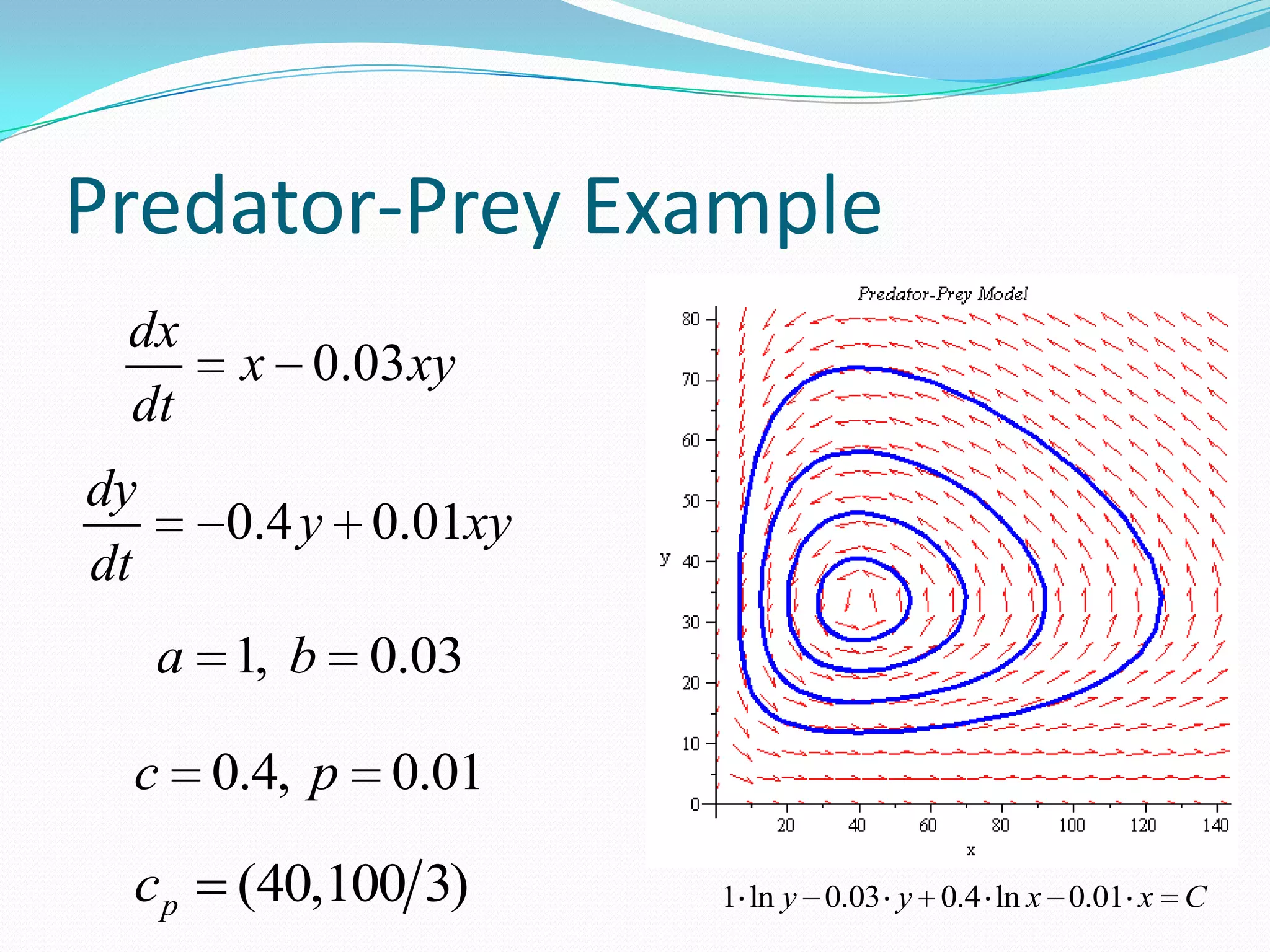
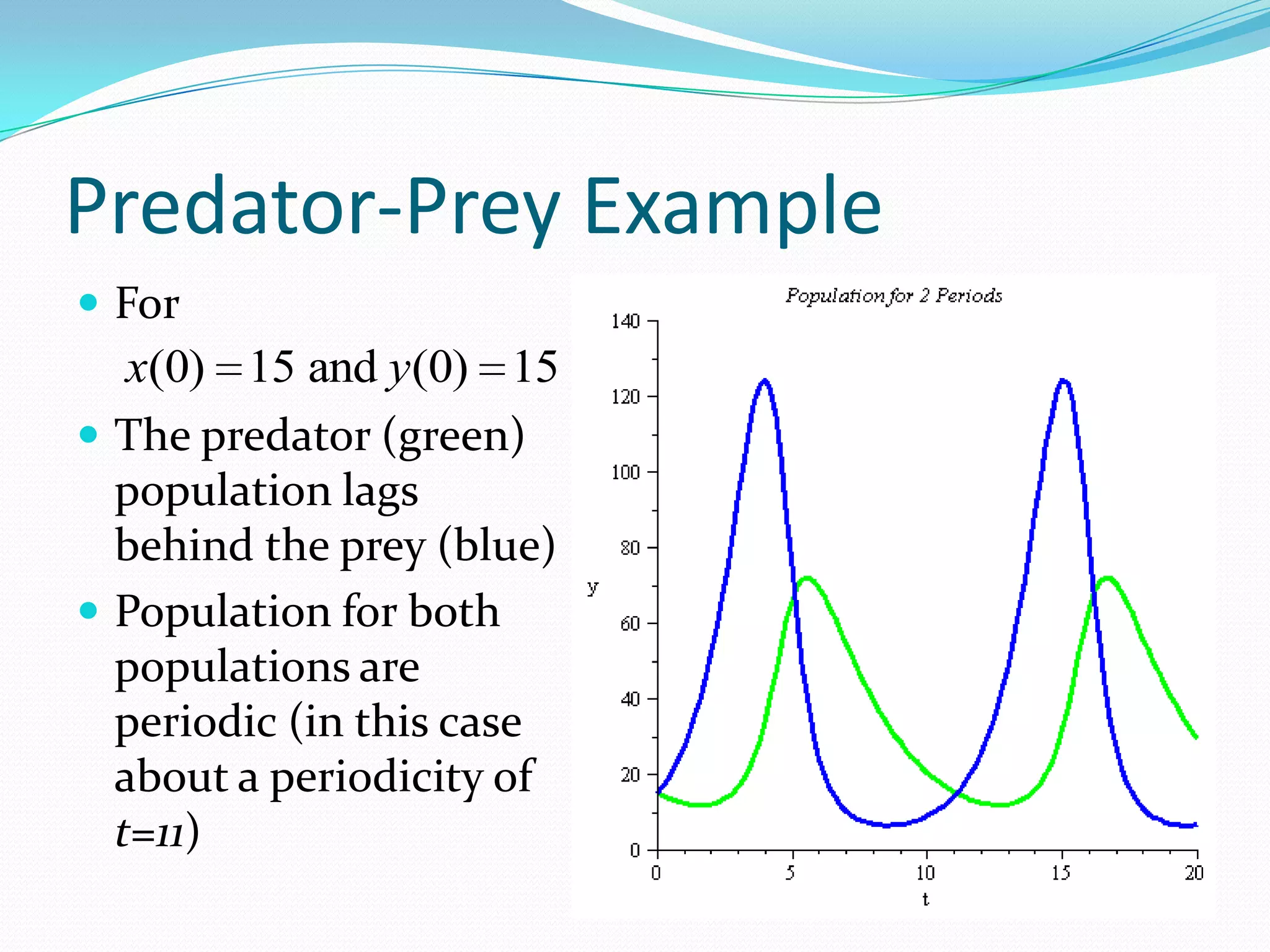
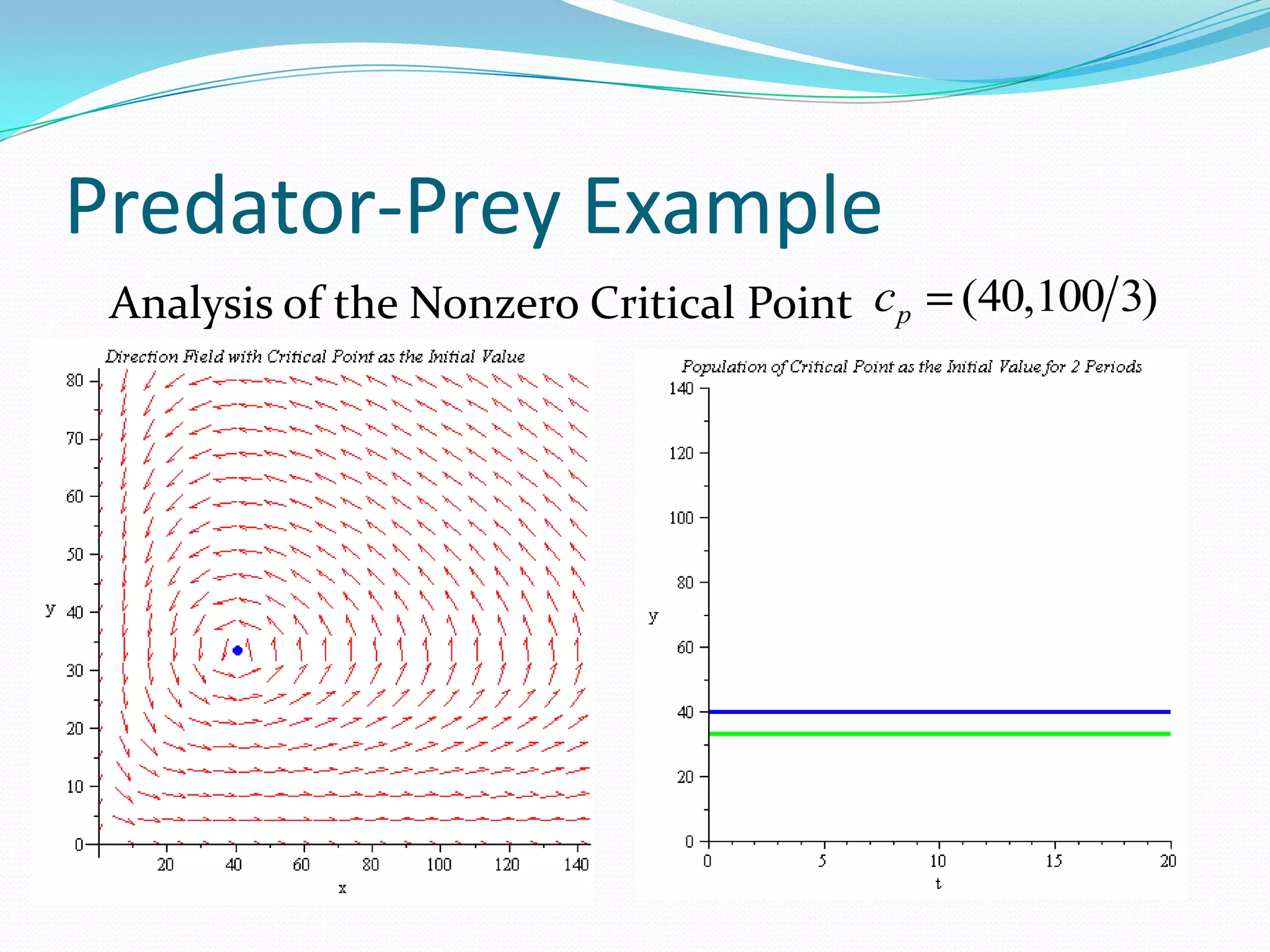
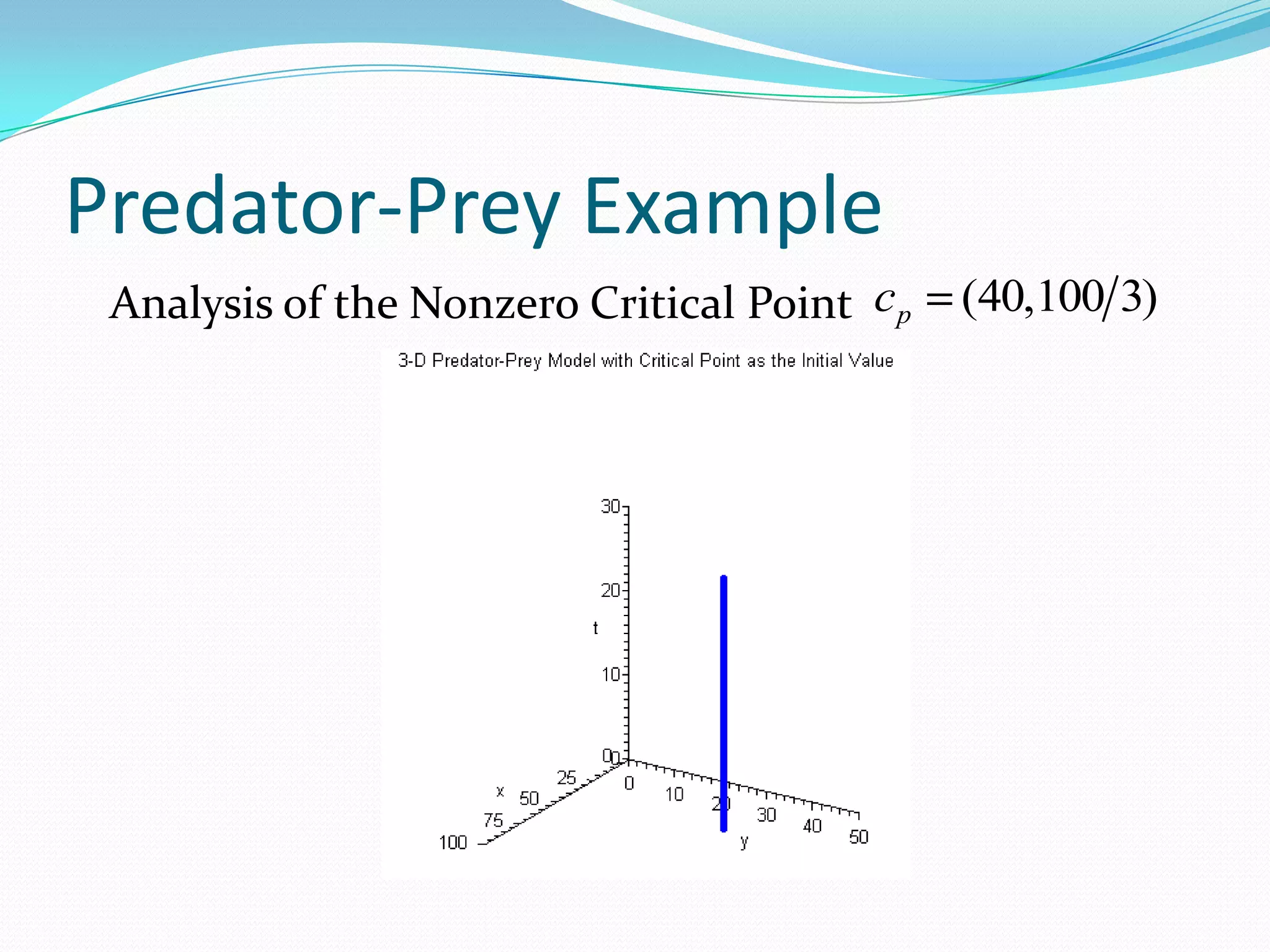
The document discusses systems of differential equations with multiple dependent variables and their solutions, including the use of eigenvalues and eigenvectors. It specifically explains the predator-prey model (Lotka-Volterra), which examines population dynamics and interactions between species, highlighting critical points and periodic behaviors. The analysis also introduces modifications for hunting effects on predator populations, leading to eventual extinction scenarios.

1. Presentation by: Joshua Dagenais

2. Systems of Differential Equations
 System involving several dependent variables ( x1, x2 ,..., xn ),
an independent variable (t), and rates of change of the
dependent variables ( x1, x2 ,..., xn )
x1 p11 (t ) x1 ... p1n (t ) xn g1 (t )
 x P(t ) x g (t )
xn pn1 (t ) x1 ... pnn (t ) xn g n (t )
x1 p11 (t )  p1n (t ) x1 g1 (t )
x  P (t )   x  g (t ) 
xn pn1 (t )  pnn (t ) xn g n (t )

3. Solutions to the System
 Solve for a 1 x 1 system
dx pt
px x ce
dt
 Solve systems second order or higher
x1 p11 (t ) x1 ... p1n (t ) xn
1 r1t n rn t
 x1 e ,..., xn e
xn pn1 (t ) x1 ... pnn (t ) xn

4. Solutions to the System
rt
 Substitute x e back into original equation
r ert P(t ) ert ( P(t ) rI ) 0
 Theorem: Let A be an n x n matrix of constant real
numbers and let X be an n-dimensional column vector.
The system of equations has nontrivial solutions, that
is, X 0 , if and only if the determinant of A is zero.
p11 (t ) r  p1n (t )
   0
pn1 (t )  pnn (t ) r

5. Solutions to the System
 Solving the determinant gives the characteristic eqn.
a0r n a1r n 1 ... an 1r an 0
 The roots , r, are the Eigenvalues r1 ,..., rn .
 Eigenvalues are used to solve for the associated
Eigenvectors, 1 ,..., n , and the specific solutions
n rnt
x(1) (t ) 1er1t ,..., x( n) (t ) e
 Specific solutions as a general solution
(1) (k ) (1) ( n)
x c1x (t )  ck x (t ) if W[ x ,..., x ] 0

6. Eigenvalues (Real & Distinct)
 Eigenvalues are of opposite signs,
the origin is a saddle point, and
trajectories are asymptotic to the
Eigenvectors
1 t 2
x(t ) c1 e c2 e 2t
2 1
 Eigenvalues are of the same signs, the
the origin is a node, and trajectories
converge to origin if Eigenvalues are
negative and vice versa if positive
7 1 4t 3 1 2t
x(t ) e e
2 1 2 3

7. Eigenvalues (Complex)
 Eigenvalues are complex with a
nonzero real point (a+bi)
 Use one of Euler’s Formulas
e( i )t e t cos( t ) i e t sin( t )
to find real-valued solutions
 The origin is called a spiral point
and trajectories converge to origin
if Eigenvalues are negative and vice
versa if positive
cos(2t ) sin(2t )
x(t ) c1et c2et
sin(2t ) cos(2t ) sin(2t ) cos(2t )

8. Eigenvalues (Repeated)
 Eigenvalues are real and
repeated with multiplicity 2
 Use x(t ) tert ert to solve
for the specific solution of
second repeated Eigenvalue
 The origin is called a improper
node and trajectories converge
to origin if Eigenvalues are x(t ) c1
1
2
e6t c2
1
2
t
0
1
e6t
negative and vice versa if positive

9. Application
 Predator-Prey Model also
known as the Lokta-Volterra
Model
 Part of mathematical ecology
that studies populations that
interact, thereby affecting each
other's growth rates
 Model represents the "natural"
growth rate and the "carrying
capacity" of the environment
(predators & prey)

10. Predator-Prey Model
 Few interactions have been
recorded in nature
 One such set of data was
taken between the
Snowshoe Hare and the
Canadian Lynx for almost
100 years
 The dominating feature is
the oscillation behavior of
both populations

11. Predator-Prey Assumptions
 x(t) will represent the number of prey at a time given
by t and y(t) will represent the number of predators at
a time also given by t.
 In the absence of the predator, the prey grows at a rate
proportional to the current population; thus
dx
ax, a 0, when y 0
dt
 In the absence of the prey, the predator dies out; thus
dy
cy, c 0, when x 0
dt

12. Predator-Prey Assumptions
 The number of encounters between predator and prey
is proportional to the product of their populations
 The growth rate of the predator is increased by a term
of the form bxy, while the growth rate of the prey is
decreased by a term –pxy
dx dy
ax bxy x(a by ) and cy pxy y( c px)
dt dt
 Critical points (when x(a by) 0 and y( c px) 0)
are (0,0) and (c / p, a / b)

13. Predator-Prey Example
dx
x 0.03 xy
dt
dy
0.4 y 0.01xy
dt
a 1, b 0.03
c 0.4, p 0.01
cp (40,100 3) 1 ln y 0.03 y 0.4 ln x 0.01 x C

14. Predator-Prey Example
 For
x(0) 15 and y(0) 15
 The predator (green)
population lags
behind the prey (blue)
 Population for both
populations are
periodic (in this case
about a periodicity of
t=11)

15. Predator-Prey Example
 Population of predators vs.
prey as t for
x(0) 15 and y(0) 15
 Prey first increase because
of small population
 Predators increase because
of abundance of food
 Heavier predation causes
prey to decrease
 Predators decrease because
of diminished food supply
 Cycle repeats itself

16. Predator-Prey Example
Analysis of the Nonzero Critical Point c p (40,100 3)

17. Predator-Prey Example
Analysis of the Nonzero Critical Point c p (40,100 3)

18. Model with Hunters Introduced
dx
ax bxy
dt
dy
cy pxy h
dt
 h is the effect of
hunting and killing a
constant amount of
predators every cycle
 Extinction eventually
occurs