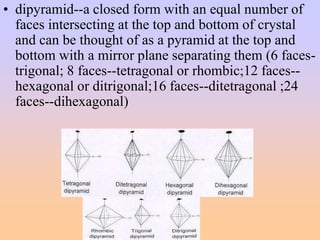
- Crystallography is the study of crystal shapes and symmetry based on how atoms combine to form geometric patterns on the smallest scale. - There are 5 main symmetry functions that determine the 32 possible crystal classes: axis of rotation, mirror plane, center of symmetry, axis of rotoinversion, and crystal forms. - Crystal forms include pinacoids, prisms, pyramids, dipyramids, and others that are characteristic of specific crystal classes and systems. Identifying crystal forms is important for determining the crystal's symmetry and class.

1. CRYSTALLOGRAPHY

2. INTRODUCTION
• crystallography is the study of crystal shapes
based on symmetry
• atoms combine to form geometric shapes on
smallest scale-- these in turn combine to form
seeable crystal shapes if mineral forms in a
nonrestrictive space (quartz crystal vs massive
quartz)
• symmetry functions present on a crystal of a
mineral allows the crystal to be categorized or
placed into one of 32 classes comprising the 6
crystal systems

5. SYMMETRY FUNCTIONS
• 1. Axis of rotation
• rotation of a crystal through 360 degrees on an axis may
reveal 2,3,4, or 6 reproductions of original face or faces--
these kinds of fold axes are:
• A2= 2-fold--a reproduction of face(s) twice
• A3= 3-fold--the same 3 times
• A4= 4-fold--the same 4 times
• A6= 6-fold--the same 6 times
• a crystal can have more than 1 kind and multiple of the
kind of fold axis each located in a perpendicular plane to
another or in some isometric classes the same at a 45
degree plane.

6. • An axis of rotation can represent only 1 YAX
• Mirror plane (symmetry plane)
• plane dividing a crystal in equal halves in which
one is a mirror image of the other
• there may be 0-9 different mirror planes on a
crystal
• designation of total mirror images on a crystal is
given by the absolute number of mirror planes
followed by a small m--four mirror images is
designated as 4m
• mirror planes, if present, occur in the same plane as
rotation axes and in the isometric, also at 45
degrees to the axes

7. • in determination of rotation axes and mirror planes, do
not count the same yAx or m more than once.
Center of symmetry
• Exists if the same surface feature is located on exact
opposite sides of the crystal and are both equal
distance from the center of crystal
• surface features include points, corners, edges, or
faces
• a crystal has or lacks a center of symmetry and if it
has, there are an infinite number of cases on the
crystal
• i is the symbol which indicates the presence of a
center of symmetry

8. Axis of rotoinversion
• is present if a reproduction of the face or faces on the
crystal is obtained through a rotation axis, then
inverting the crystal
• if done so on an A3 axis, the symmetry is designated
as an A3 with a bar above
• there can be a barA3, barA4 or barA6 but only one of
these roto inversion axes can exist on a crystal if
present
• although an important symmetry function, it is not
necessary to use it to categorize crystals---if present
a combination of the other 3 symmetry functions
substitutes for it
• a barA3 is equivalent to an A3 + an i; a barA4, to an A2 ; a
barA6 to an A3+ m

9. • If the total symmetry of crystal is ascertained, (
substitute symmetries if an axis of roto inversion
exists) the crystal can be categorized in one of 32
classes---see table
• mother nature limits the combinations of symmetry
functions which can occur with crystals--for
example;
• an A6 cannot be present with an A4 and vice versa
• an A6 cannot be present with an A3 and vice versa
• the number or kind of symmetry function(s) can lend
important information
• the presence of a 1A4 signifies a tetragonal class crystal
and if more A4 there must be 3A4, then belonging to the
isomeric class

10. • presence of 1A3 signifies a hexagonal class, if more,
there must be 4A3 present and belongs in an isometric
class
• HOLOHEDRAL refers to the respective class in
each crystal system possessing the highest (most
complex) symmetry
• even though crystals may not appear to look the
same, they may have the exact same symmetry
• NOW LET’S spend time on determining crystal
symmetry on wooden blocks and to which crystal
class and system each belongs

11. CRYSTAL FORMS
• a group of faces on a crystal related to the same symmetry
functions
• the faces of the group are usually the same size and shape
on the crystal
• recognition of crystal forms can help determine the
symmetry functions present on a crystal and vice versa
• forms related to non isometric classes are quite different
than those related to isometric classes
• since more than one form can exist on a crystal, it is more
difficult to ascertain each form in the “full form”--each “full
form” will be shown in the following presentation--also note
the symmetry related to the form--see page 127 for axes
symbols

12. Rotation axis Symbol
or for
Inversion axis axis

13. • Non-isometric forms
• pedion--a single face
• pinacoid--an open form comprised of 2 parallel faces--
many possible locations on crystal
• dome--open form with 2 non parallel faces with respect
to a mirror plane and A2--located at top of crystal
• sphenoid--two nonparallel faces related to an A2--located
at top of crystal

14. • prism-- open form of 3 (trigonal), 4
(tetragonal, monoclinc or orthorhombic), 6 (
hexagonal or ditrigonal), 8 (ditetragonal), or
12 ( dihexagonal) faces all parallel to same
axis and except for some in the monoclinic,
that axis is the highest fold axis--most prism
faces are located on side of crystal

15. • pyramid--open form with 3 (trigonal), 4
(tetragonal or orthorhombic), 6 (hexagonal or
ditrigonal), 8 (ditetragonal) or 12 (dihexagonal)
nonparallel faces meeting at the top of a crystal

16. • dipyramid--a closed form with an equal number of
faces intersecting at the top and bottom of crystal
and can be thought of as a pyramid at the top and
bottom with a mirror plane separating them (6 faces-
trigonal; 8 faces--tetragonal or rhombic;12 faces--
hexagonal or ditrigonal;16 faces--ditetragonal ;24
faces--dihexagonal)

17. • trapezohedron--a closed form with 6, 8, or 12 faces
with 3 (trigonal), 4 (tetragonal) or 6 (hexagonal)
upper faces offset with each of the same number at
bottom--no mirror plane separates top set from
bottom--note the 3 sets of A2 at the sides

18. • scalenohedron--a closed form with 8
(tetragonal) or 12 (hexagonal) faces grouped
in symmetrical pairs--note the inversion 4
fold and inversion 3 fold and A2 axes
associated with each

19. • disphenoid--a closed form with 2 upper
faces alternating with 2 lower faces offset
by 90 degrees

20. ISOMETRIC FORMS
• Many of these forms are based on a triad of isometric
forms, the cube (hexahedron), octahedron, and tetrahedron--
the name of a form often includes the suffix of the triad with
a prefix
• cube (hexahedron)--6 equal faces intersecting at 90
degrees
• octahedron--8 equilateral triangular faces
• tetrahedron--4 equilateral triangular faces

21. • dodecahedron--12 rhombed faces
• tetrahexahedron--24 isosceles triangular faces--4
faces on each basic hexahedron face
• trapezohedron--24 trapezium shaped faces
• trisoctahedron--24 isosceles triangular faces--3
faces on each octahedron face

22. • hexoctahedron--48 triangular faces--6 faces on each
basic octahedron face
• tristetrahedron--12 triangular faces--3 faces on each
basic tetrahedron face
• deltoid dodecahedron--12 faces corresponding to 1/2
of trisoctahedron faces
• hextetrahedron--24 faces--6 faces on each basic
tetrahedron face

23. • diploid--24 faces
• pyritohedron--12 pentagonal faces

24. • It is possible to identify the class of the crystal in
some cases based on the form(s) present--this can be
done with much practice in identifying crystal forms
• refer to the table with all possible forms which can
exist in a crystal class of each crystal system--
examples of key forms present on crystals are:
• the rhombic dipyramid can only occur in the rhombic
dipyramidal class
• the ditrigonal dipyramid can only occur in the ditrigonal
dipyramidal class
• the hextetrahedron can occur only in the hextetrahedral
class
• the tetrahexahedron can occur only in the hextetrahedral
class
• crystal class names are based on the most outstanding
form possible--NOW, GO TO IT