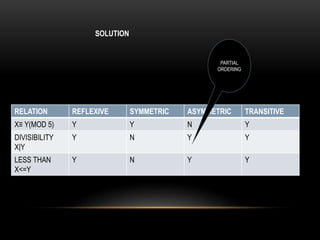
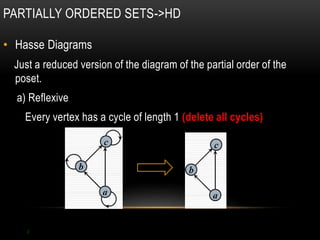
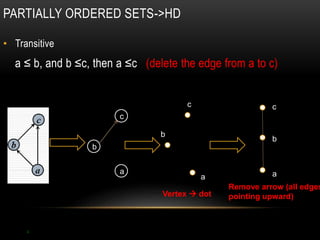
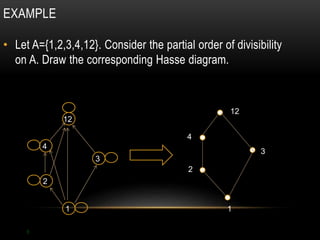
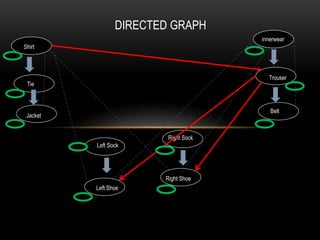
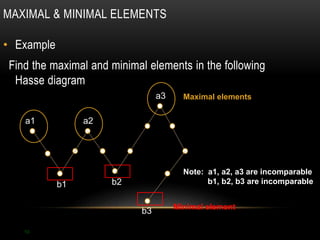
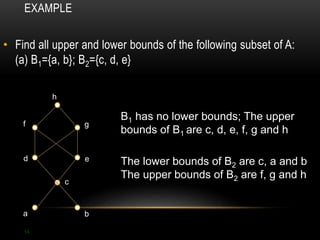
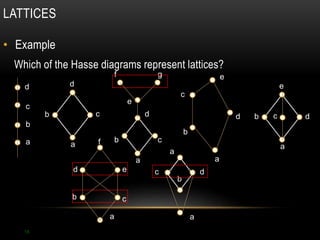
The document discusses partial ordering and lattices. It defines key concepts like reflexive, symmetric, antisymmetric, and transitive relations. It introduces Hasse diagrams as a way to visualize partial orders and uses examples to demonstrate extremal elements, bounds, and lattices. Lattices are partial orders where every two elements have a greatest lower bound and least upper bound. The document provides examples of determining these bounds and whether a partial order represents a lattice.

1. INTRODUCTION TO PARTIAL ORDERING
RELATION REFLEXIVE SYMMETRIC ASYMMETRIC TRANSITIVE
X≡ Y(MOD 5)
DIVISIBILITY
X|Y
LESS THAN
X<=Y

2. PARTIAL
ORDERING
SOLUTION
RELATION REFLEXIVE SYMMETRIC ASYMMETRIC TRANSITIVE
X≡ Y(MOD 5) Y Y N Y
DIVISIBILITY
Y N Y Y
X|Y
LESS THAN
X<=Y
Y N Y Y

3. PARTIALLY ORDERED SETS->HD
• Hasse Diagrams
Just a reduced version of the diagram of the partial order of the
poset.
a) Reflexive
Every vertex has a cycle of length 1 (delete all cycles)
3

4. PARTIALLY ORDERED SETS->HD
• Transitive
a ≤ b, and b ≤c, then a ≤c (delete the edge from a to c)
4
b
c
a
a
b
c
Vertex  dot
c
b
a
Remove arrow (all edges
pointing upward)

5. EXAMPLE
• Let A={1,2,3,4,12}. Consider the partial order of divisibility
on A. Draw the corresponding Hasse diagram.
5
12
4
2
1
3
12
4
2
1
3

6. Shirt
innerwear
Tie
Jacket
Trouser
Belt
HASSE DIAGRAM
Left Sock Right Sock
Left Shoe Right Shoe

7. Shirt
innerwear
Tie
Jacket
Trouser
Belt
DIRECTED GRAPH
Left Shoe
Right Shoe
Left Sock
Right Sock

8. EXTREMAL ELEMENTS & BOUNDS
• Lets assume a poset (A, p) represented by a hasse diagram as shown.
• Binary Relation : ( a divides b)
• Set is = {1,2…..6}
6 3
4 5
2 1

9. EXTREMAL ELEMENTS & BOUNDS
• 1 --- > Least element in Poset ( < everything)
• No greatest element in this Poset( as defined by BR)
• 4,6 Are maximal Elements
• 1 is Minimal Elements
• For 2,3 ----- > 6 is the LEAST UPPER BOUND
• ------ >1 is the GREATEST LOWER BOUND
• For 3,5 ----- > NO LEAST UPPER BOUND
• ------ >1 is GREATEST LOWER BOUND
• For 4,3 ----- > NO LEAST UPPER BOUND
• ------ >1 is GREATEST LOWER BOUND

10. MAXIMAL & MINIMAL ELEMENTS
• Example
Find the maximal and minimal elements in the following
Hasse diagram
a1 a2
10
a3
b1 b2
b3
Maximal elements
Note: a1, a2, a3 are incomparable
b1, b2, b3 are incomparable
Minimal element

11. • Greatest element (Maximal )
An element a in A is called a greatest element of A if
x ≤ a for all x in A.
• Least element (Minimal)
An element a in A is called a least element of A if
a ≤ x for all x in A.
Note: an element a of (A, ≤ ) is a greatest (or least) element if
and only if it is a least (or greatest) element of (A, ≥ )
11

12. THEOREM
A poset has at most one greatest element and at most one least
element.
Proof:
Support that a and b are greatest elements of a poset A. since b is a
greatest element, we have a ≤ b;
since a is a greatest element, we have b ≤ a; thus
a=b by the antisymmetry property. so, if a poset has a greatest element, it
only has one such element.
This is true for all posets, the dual poset (A, ≥) has at most one greatest element,
so (A, ≤) also has at most one least element.
12

13. • Unit element
The greatest element of a poset, if it exists, is denoted by I
and is often called the unit element.
• Zero element
The least element of a poset, if it exists, is denoted by 0 and
is often called the zero element.
13

14. EXAMPLE
• Find all upper and lower bounds of the following subset of A:
(a) B1={a, b}; B2={c, d, e}
14
h
f g
d e
c
a b
B1 has no lower bounds; The upper
bounds of B1 are c, d, e, f, g and h
The lower bounds of B2 are c, a and b
The upper bounds of B2 are f, g and h

15. BOUNDS
Let A be a poset and B a subset of A,
• Least upper bound
An element a in A is called a least upper bound of B, denoted
by (LUB(B)), if a is an upper bound of B and a ≤a’,
whenever a’ is an upper bound of B.
• Greatest lower bound
An element a in A is called a greatest lower bound of B,
denoted by (GLB(B)), if a is a lower bound of B and a’ ≤ a,
whenever a’ is a lower bound of B.
15

16. EXAMPLE
• Let A={1,2,3,…,11} be the poset whose Hasse diagram is
shown below. Find the LUB and GLB of B={6,7,10}, if they
exist.
5 6 7 8
16
1
2
3
4
10
9
11 The upper bounds of B are 10, 11, and
LUB(B) is 10 (the first vertex that can be
Reached from {6,7,10} by upward paths )
The lower bounds of B are 1,4, and
GLB(B) is 4 (the first vertex that can be
Reached from {6,7,10} by downward paths )

17. LATTICES
A lattice is a poset (L, ≤) in which every subset {a, b}
consisting of two elements has a least upper bound and a
greatest lower bound. We denote :
LUB({a, b}) by a∨ b (the join of a and b)
GLB({a, b}) by a ∧b (the meet of a and b)
17

18. LATTICES
• Example
Which of the Hasse diagrams represent lattices?
d
c
b
a
18
f g
b c
a
d
e
a
c
b
e
d
a
b c
e
d
d
b c
a
d e
b c
a
f
c d
a
b
a

19. LATTICES: EXAMPLE
• Is the example from before
a lattice?
g h
b d
a
i
f
e
c
j
• No, because the pair
{b,c} does not have a
least upper bound

20. LATTICES: EXAMPLE
• What if we modified it as
shown here?
g h
b d
a
i
f
e
c
j
• Yes, because for any
pair, there is an lub & a
glb

21. Distributive lattices

22. THANK YOU
-- Aarti Jivrajani
-- Debarati Das