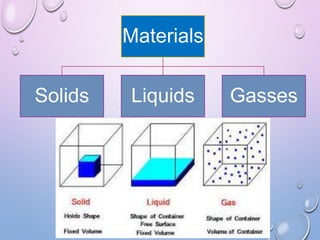
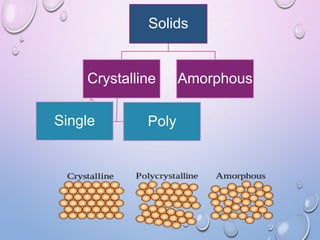
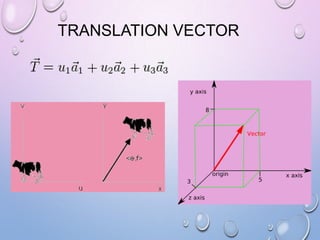
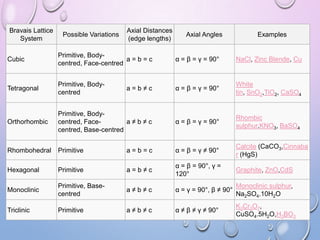
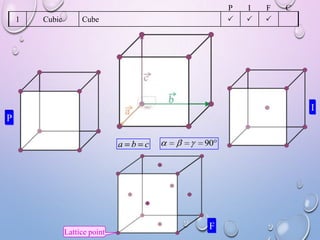
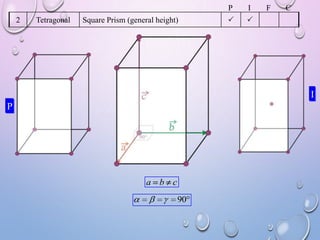
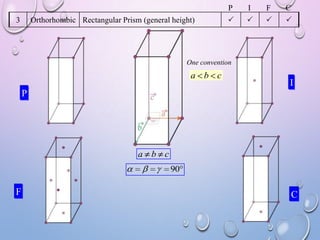
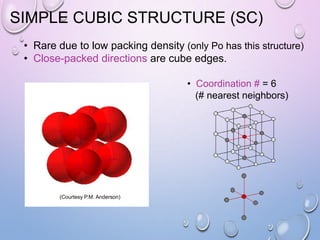
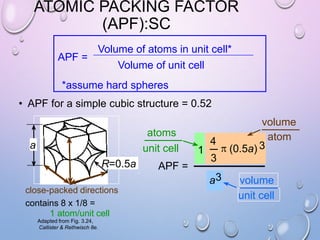
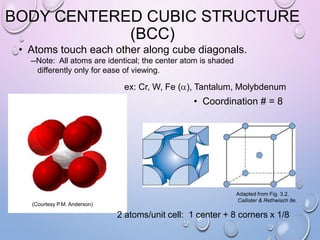
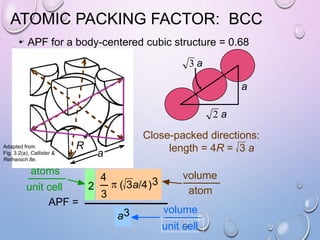
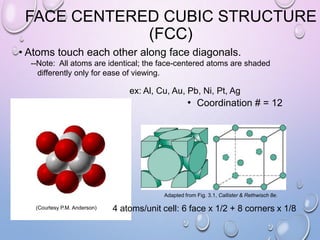
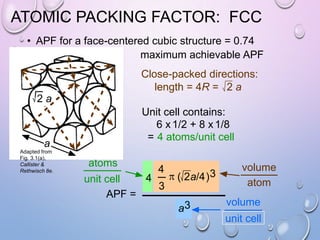
This document summarizes a seminar presentation on crystal structure. It introduces key concepts like translation vectors, basis and unit cells, Bravais and space lattices, fundamental quantities like nearest neighbor distance and coordination number. It describes the 7 crystal systems and 14 Bravais lattices. It discusses packing in simple cubic, body centered cubic and face centered cubic structures. It also covers Miller indices for directions and planes, and the formula for inter-planar spacing in cubic crystals.





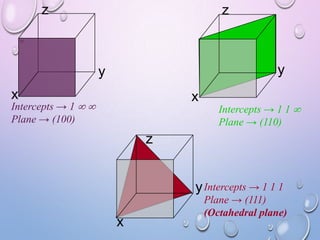
![MILLER INDICES
• INDICES ARE WRITTEN IN SQUARE BRACKETS WITHOUT
COMMAS (EX: [HKL])
• NEGATIVE VALUES ARE WRITTEN WITH A BAR OVER THE
INTEGER.
[hkl]
• EX: IF H<0 THEN THE DIRECTION IS
•](https://image.slidesharecdn.com/crystralstructure-131016053449-phpapp01/85/Crystral-structure-23-320.jpg)

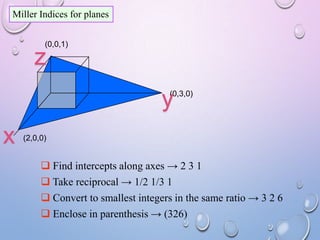
![MILLER INDICES
• CLEAR FRACTIONS DUE TO THE RECIPROCAL,
BUT DO NOT REDUCE TO LOWEST INTEGER
VALUES.
• PLANES ARE WRITTEN IN PARENTHESES, WITH
BARS OVER THE NEGATIVE INDICES. [hkl]
• EX: (HKL) OR IF H<0 THEN IT BECOMES](https://image.slidesharecdn.com/crystralstructure-131016053449-phpapp01/85/Crystral-structure-26-320.jpg)