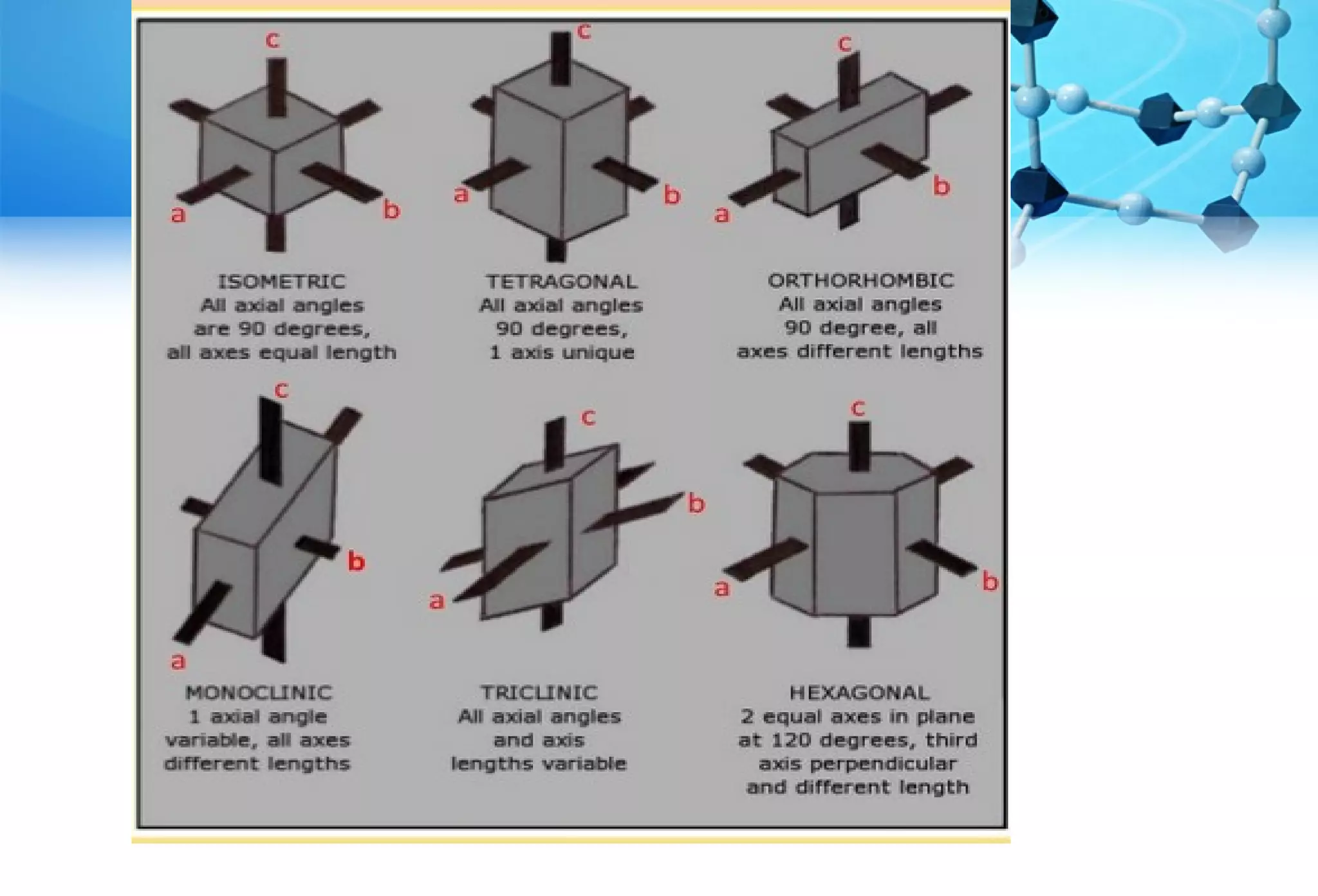
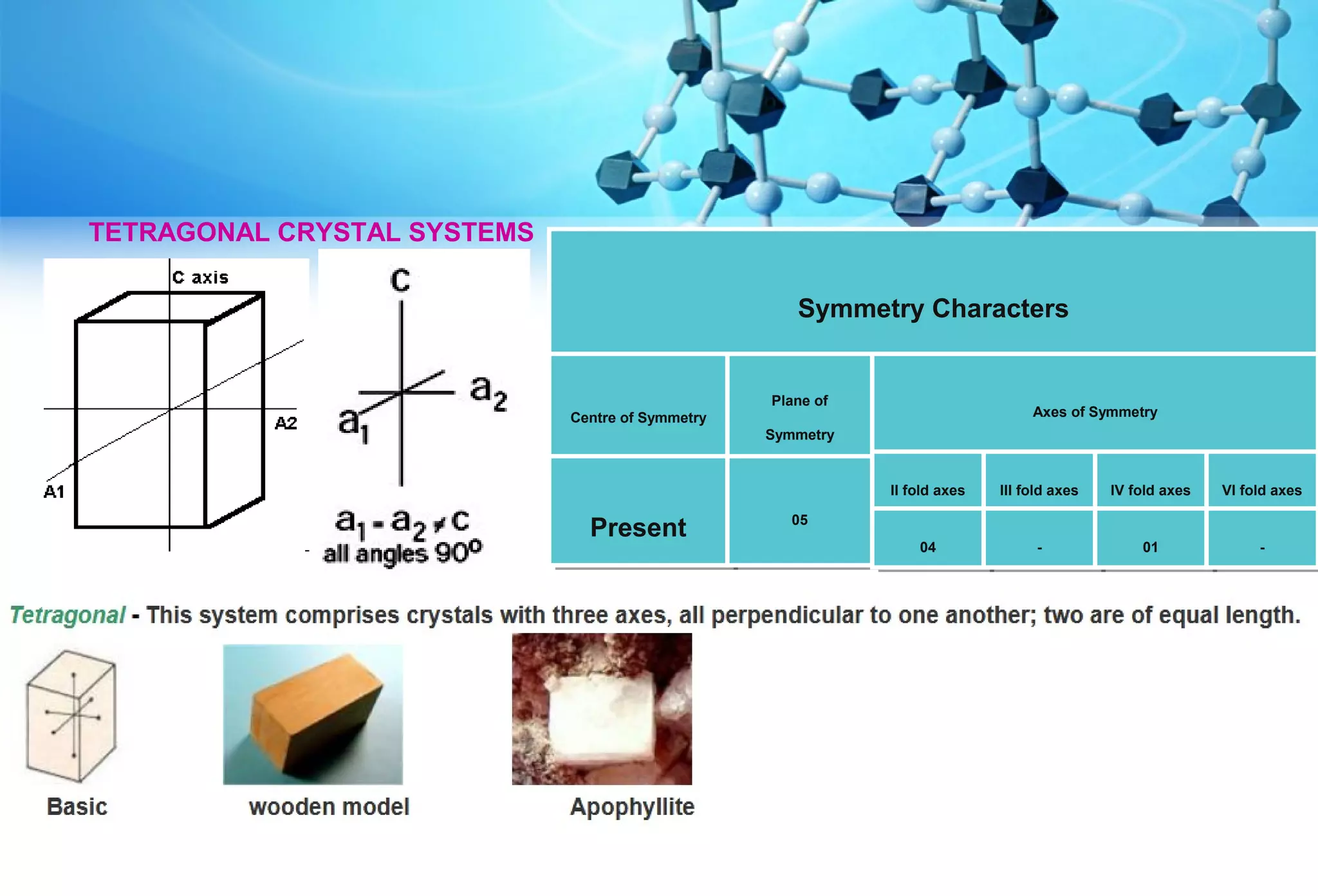
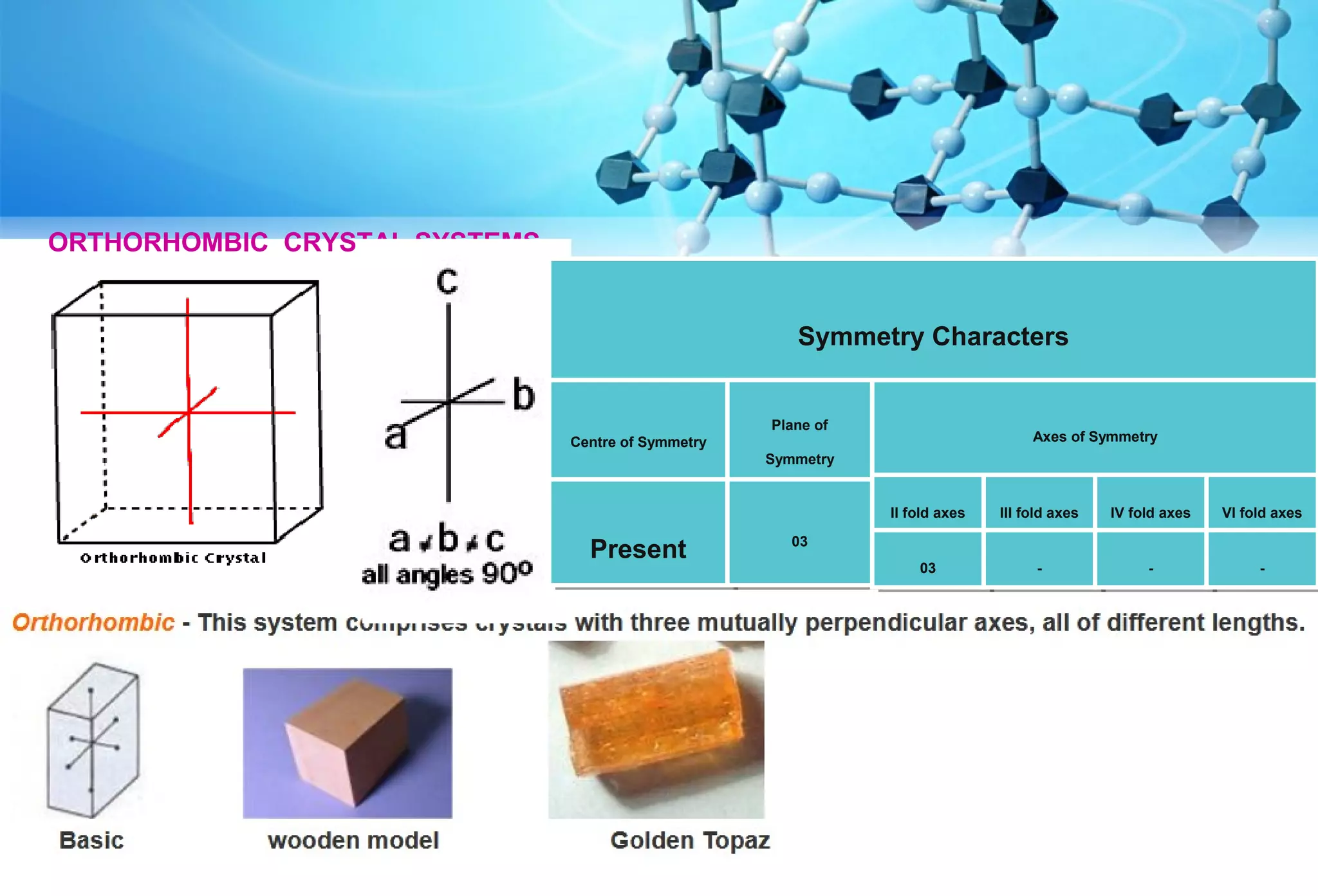
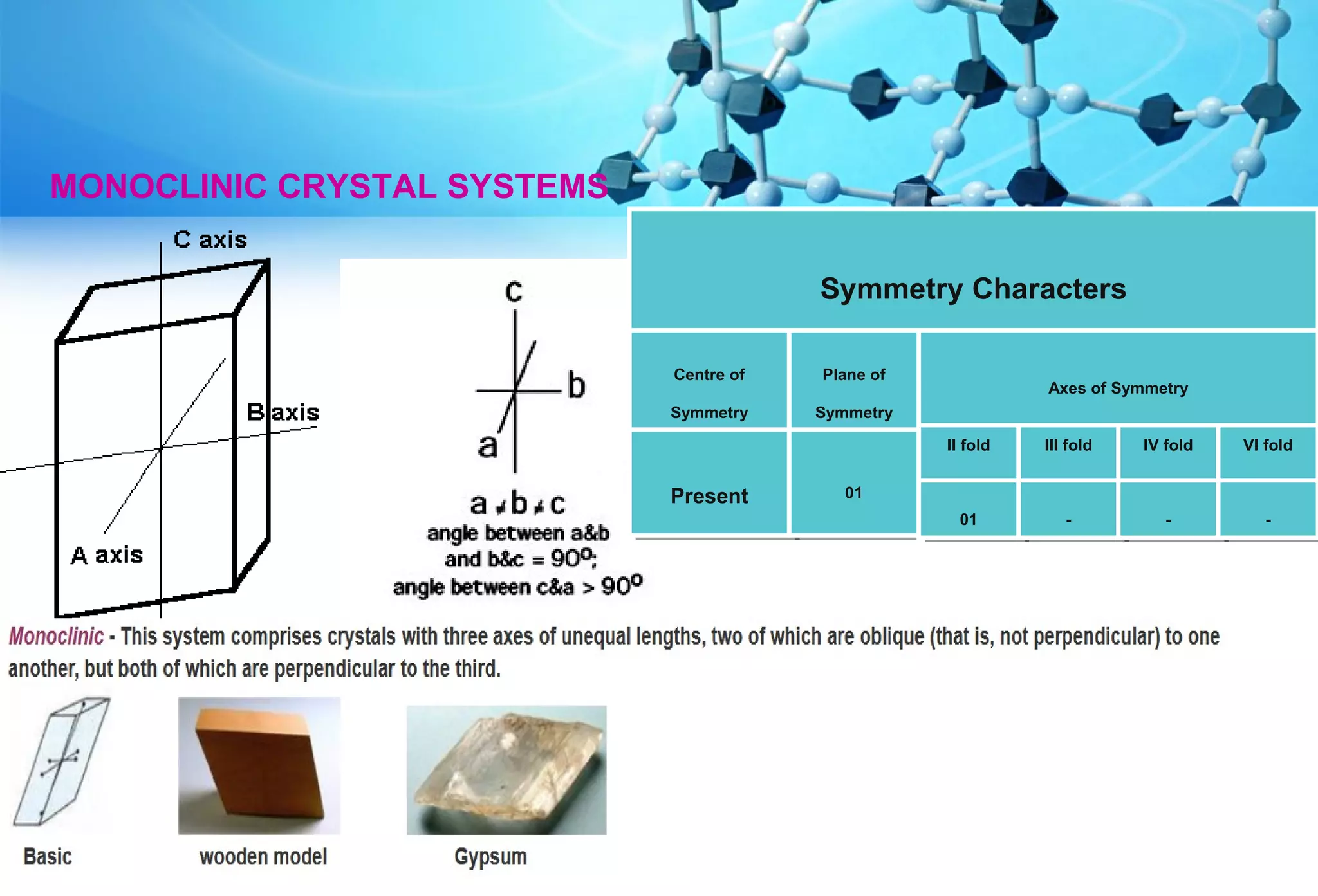
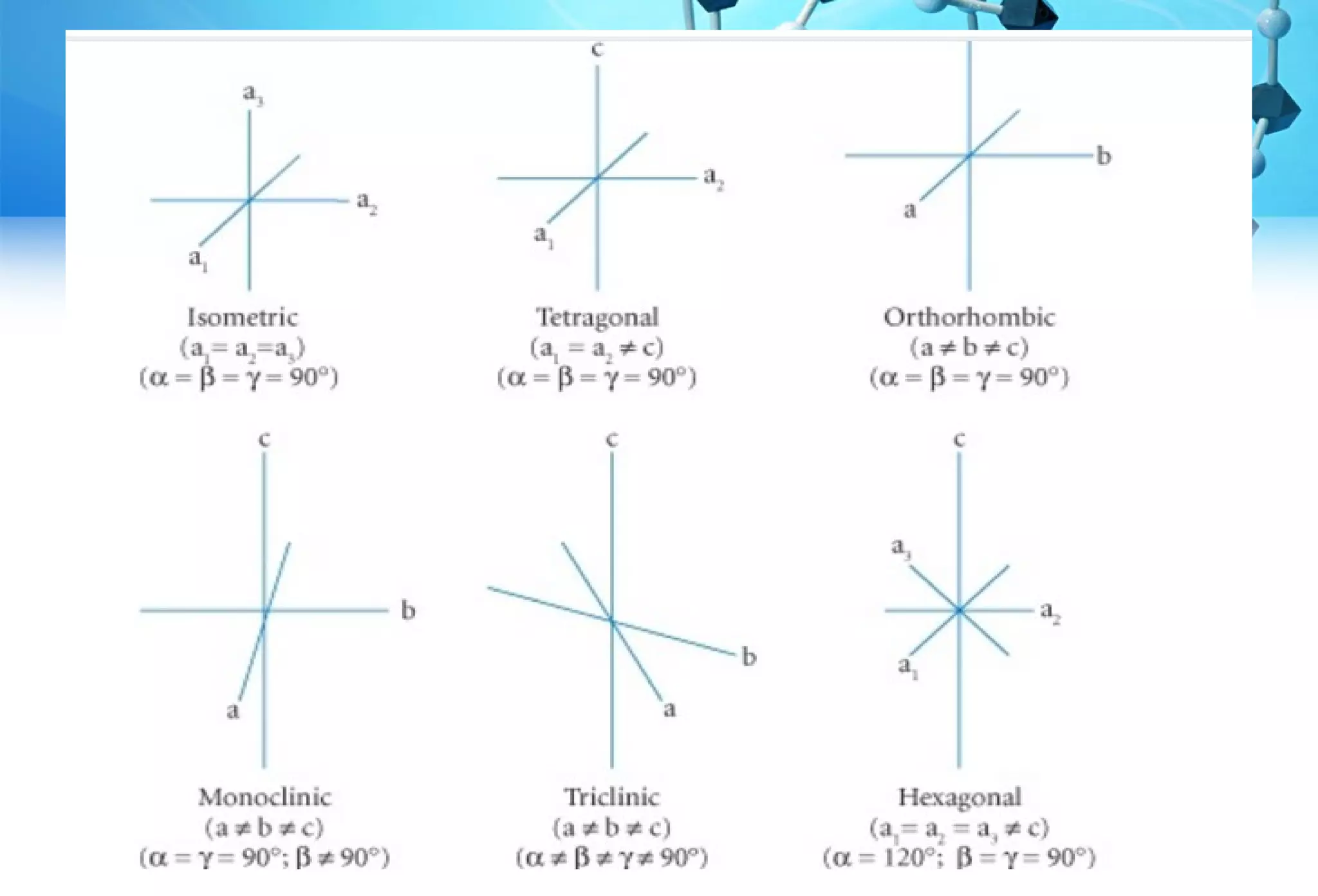
This document discusses crystallography and crystal structure. It defines key terms like crystalline solids, amorphous solids, unit cell, crystal lattice, crystallographic planes, and Miller indices. It describes the seven crystal systems (cubic, tetragonal, orthorhombic, monoclinic, triclinic, hexagonal, trigonal) based on their symmetry characteristics. It also discusses crystal forms, symmetry operations like rotation axes and planes of symmetry, and the notation used to describe crystal planes and orientations.