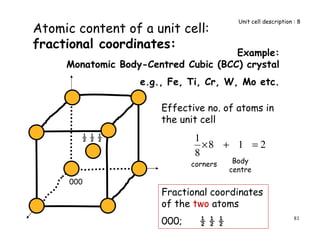
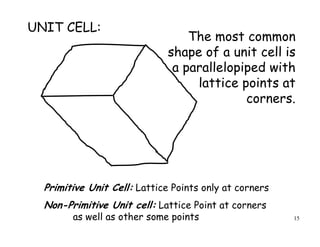
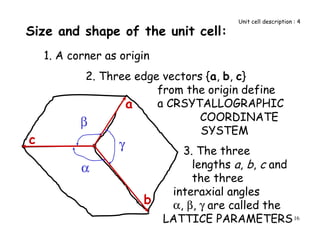
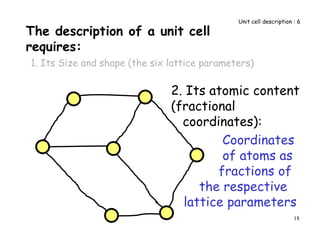
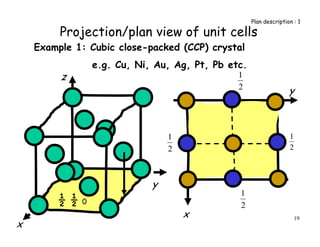
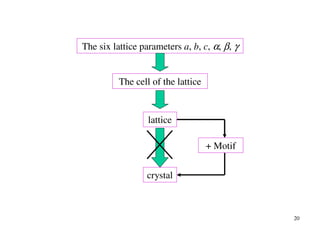
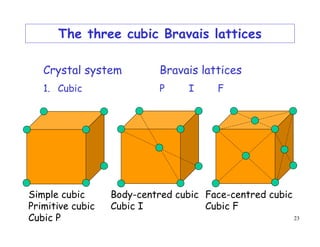
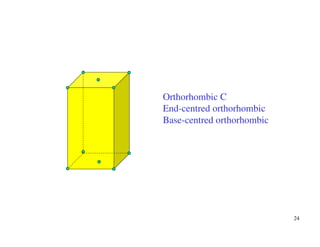
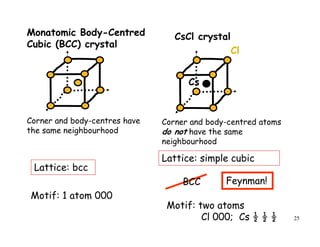
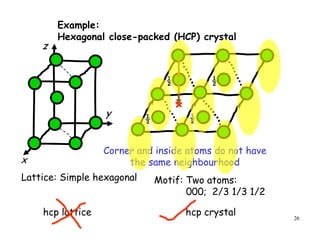
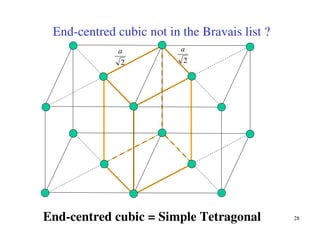
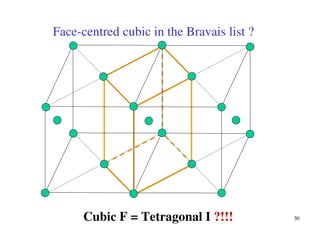
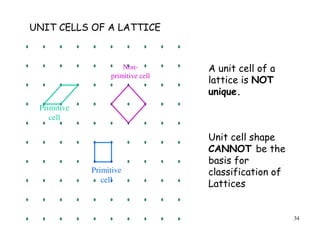
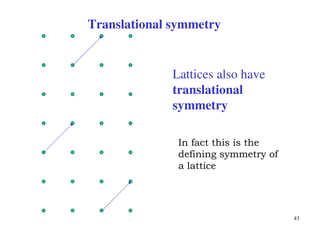
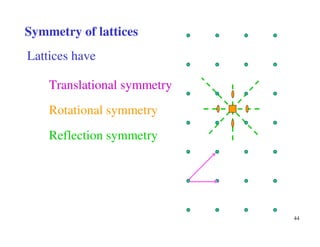
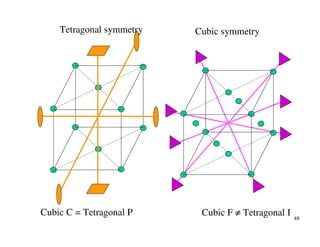
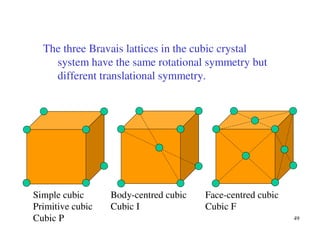
The document provides an introduction to basic crystallography concepts including crystals, lattices, motifs, unit cells, and Miller indices. It discusses that a crystal is defined as a periodically arranged structure of atoms or molecules in space. A lattice refers to the underlying periodic arrangement of points, while a motif represents the atom or group of atoms associated with each lattice point. Crystals are classified into 7 crystal systems and 14 Bravais lattices based on their rotational and translational symmetry properties. Miller indices are used to describe directions and planes in a crystal lattice using small integers.

1. DST-SERC School on Texture and Microstructure
BASIC CRYSTALLOGRAPHY
Rajesh Prasad
Department of Applied Mechanics
Indian Institute of Technology
New Delhi 110016
rajesh@am.iitd.ac.in

2. 2
Contents
Crystal, Lattice and Motif
Unit cells, Lattice Parameters and Projections
Miller Indices & Miller-Bravais Indices
Directions and Planes
Classification of Lattices:
7 crystal systems
14 Bravais lattices
Reciprocal lattice

3. 3
A 3D translationaly
periodic arrangement
of atoms in space is
called a crystal.
Crystal ?

4. 4
Lattice?
A 3D translationally
periodic arrangement
of points in space is
called a lattice.

5. 5
A 3D
translationally
periodic
arrangement
of atoms
Crystal
A 3D
translationally
periodic
arrangement of
points
Lattice

6. 6
What is the relation between
the two?
Crystal = Lattice + Motif
Motif or basis: an atom or
a group of atoms associated
with each lattice point

7. 7
Crystal=lattice+basis
Lattice: the underlying periodicity of
the crystal,
Basis: atom or group of atoms
associated with each lattice points
Lattice: how to repeat
Motif: what to repeat

8. 8
A 3D translationally periodic
arrangement of points
Each lattice point in a lattice
has identical neighbourhood of
other lattice points.
Lattice

9. 9
+
Love Pattern
(Crystal)
Love Lattice + Heart
(Motif)
=
=
Lattice + Motif = Crystal
Love Pattern

10. 10
Air,
Water
and
Earth
by
M.C.
Esher

11. 11
Every
periodic
pattern
(and hence
a crystal)
has a
unique
lattice
associated
with it

12. 12

13. 13
Contents
Crystal, Lattice and Motif
Unit cells, Lattice Parameters and Projections
Miller Indices & Miller-Bravais Indices
Directions and Planes
Classification of Lattices:
7 crystal systems
14 Bravais lattices
Reciprocal lattice

14. 14
Translational Periodicity
One can select a small volume of
the crystal which by periodic
repetition generates the entire
crystal (without overlaps or gaps)
Unit
Cell
Unit cell description : 1

15. 15
The most common
shape of a unit cell is
a parallelopiped with
lattice points at
corners.
UNIT CELL:
Primitive Unit Cell: Lattice Points only at corners
Non-Primitive Unit cell: Lattice Point at corners
as well as other some points

16. 16
Size and shape of the unit cell:
1. A corner as origin
2. Three edge vectors {a, b, c}
from the origin define
a CRSYTALLOGRAPHIC
COORDINATE
SYSTEM
3. The three
lengths a, b, c and
the three
interaxial angles
α, β, γ are called the
LATTICE PARAMETERS
α
β
γ
a
b
c
Unit cell description : 4

17. 17
7 crystal Systems
Crystal System Conventional Unit Cell
1. Cubic a=b=c, α=β=γ=90°
2. Tetragonal a=b≠c, α=β=γ=90°
3. Orthorhombic a≠b≠c, α=β=γ=90°
4. Hexagonal a=b≠c, α=β= 90°, γ=120°
5. Rhombohedral a=b=c, α=β=γ≠90°
OR Trigonal
6. Monoclinic a≠b≠c, α=β=90°≠γ
7. Triclinic a≠b≠c, α≠β≠γ
Unit cell description : 5

18. 18
The description of a unit cell
requires:
1. Its Size and shape (the six lattice parameters)
2. Its atomic content
(fractional
coordinates):
Coordinates
of atoms as
fractions of
the respective
lattice parameters
Unit cell description : 6

19. 19x
y
Projection/plan view of unit cells
½ ½ 0
Example 1: Cubic close-packed (CCP) crystal
e.g. Cu, Ni, Au, Ag, Pt, Pb etc.
2
1
2
1
2
1
2
1
x
y
z
Plan description : 1

20. 20
The six lattice parameters a, b, c, α, β, γ
The cell of the lattice
lattice
crystal
+ Motif

21. 21
Contents
Crystal, Lattice and Motif
Unit cells, Lattice Parameters and Projections
Miller Indices & Miller-Bravais Indices
Directions and Planes
Classification of Lattices:
7 crystal systems
14 Bravais lattices
Reciprocal lattice

22. 22
14 Bravais lattices divided into seven crystal systems
Crystal system Bravais lattices
1. Cubic P I F
2. Tetragonal P I
3. Orthorhombic P I F C
4. Hexagonal P
5. Trigonal P
6. Monoclinic P C
7. Triclinic P
P: Primitive
(lattice points only at
the 8 corners of the
unit cell)
I: Body-centred (lattice
points at the corners + one
lattice point at the centre of
the unit cell)
F: Face-centred
(lattice points at the
corners + lattice
points at centres of
all faces of the unit
cell)
C: End-centred or
base-centred
(lattice points at the
corners + lattice
points at the centres of
a pair of opposite
faces)

23. 23
The three cubic Bravais lattices
Crystal system Bravais lattices
1. Cubic P I F
Simple cubic
Primitive cubic
Cubic P
Body-centred cubic
Cubic I
Face-centred cubic
Cubic F

24. 24
Orthorhombic C
End-centred orthorhombic
Base-centred orthorhombic

25. 25
Monatomic Body-Centred
Cubic (BCC) crystal
Lattice: bcc
CsCl crystal
Lattice: simple cubic
BCC Feynman!
Corner and body-centres have
the same neighbourhood
Corner and body-centred atoms
do not have the same
neighbourhood
Motif: 1 atom 000
Motif: two atoms
Cl 000; Cs ½ ½ ½
Cs
Cl

26. 26
½
½½
½
Lattice: Simple hexagonal
hcp lattice hcp crystal
Example:
Hexagonal close-packed (HCP) crystal
x
y
z
Corner and inside atoms do not have
the same neighbourhood
Motif: Two atoms:
000; 2/3 1/3 1/2

27. 27
14 Bravais lattices divided into seven crystal
systems
Crystal system Bravais lattices
1. Cubic P I F
2. Tetragonal P I
3. Orthorhombic P I F C
4. Hexagonal P
5. Trigonal P
6. Monoclinic P C
7. Triclinic P
?

28. 28
End-centred cubic not in the Bravais list ?
End-centred cubic = Simple Tetragonal
2
a
2
a

29. 29
14 Bravais lattices divided into seven crystal
systems
Crystal system Bravais lattices
1. Cubic P I F C
2. Tetragonal P I
3. Orthorhombic P I F C
4. Hexagonal P
5. Trigonal P
6. Monoclinic P C
7. Triclinic P

30. 30
Face-centred cubic in the Bravais list ?
Cubic F = Tetragonal I ?!!!

31. 31
14 Bravais lattices divided into seven crystal
systems
Crystal system Bravais lattices
1. Cubic P I F C
2. Tetragonal P I
3. Orthorhombic P I F C
4. Hexagonal P
5. Trigonal P
6. Monoclinic P C
7. Triclinic P

32. 32
Couldn’t
find his
photo on
the net
1811-1863
Auguste Bravais
1850: 14 lattices1835: 15 lattices
ML Frankenheim
1801-1869
24 March 2008:
13 lattices !!!
DST-SERC
School
X
1856: 14 lattices
History:

33. 33
Why can’t the Face-
Centred Cubic lattice
(Cubic F) be considered
as a Body-Centred
Tetragonal lattice
(Tetragonal I) ?

34. 34
Primitive
cell
Primitive
cell
Non-
primitive cell
A unit cell of a
lattice is NOT
unique.
UNIT CELLS OF A LATTICE
Unit cell shape
CANNOT be the
basis for
classification of
Lattices

35. 35
What is the basis for
classification of lattices
into
7 crystal systems
and
14 Bravais lattices?

36. 36
Lattices are
classified on the
basis of their
symmetry

37. 37
What is
symmetry?

38. 38
If an object is brought into self-
coincidence after some
operation it said to possess
symmetry with respect to that
operation.
Symmetry

39. 39
NOW NO SWIMS ON MON

40. 40
Rotational symmetry
http://fab.cba.mit.edu/

41. 41
If an object come into self-coincidence through smallest
non-zero rotation angle of θ then it is said to have an n-
fold rotation axis where
θ
0
360
=n
θ=180°
θ=90°
Rotation Axis
n=2 2-fold rotation axis
n=4 4-fold rotation axis

42. 42
Reflection (or mirror symmetry)

43. 43
Lattices also have
translational
symmetry
Translational symmetry
In fact this is the
defining symmetry of
a lattice

44. 44
Symmetry of lattices
Lattices have
Rotational symmetry
Reflection symmetry
Translational symmetry

45. 45
The group of all symmetry elements of a
crystal except translations (e.g. rotation,
reflection etc.) is called its POINT
GROUP.
The complete group of all symmetry
elements of a crystal including translations
is called its SPACE GROUP
Point Group and Space Group

46. 46
Classification of lattices
Based on the space group symmetry, i.e.,
rotational, reflection and translational
symmetry
⇒ 14 types of lattices
⇒ 14 Bravais lattices
Based on the point group symmetry alone
⇒ 7 types of lattices
⇒ 7 crystal systems

47. 47
7 crystal Systems
System Required symmetry
• Cubic Three 4-fold axis
• Tetragonal one 4-fold axis
• Orthorhombic three 2-fold axis
• Hexagonal one 6-fold axis
• Rhombohedral one 3-fold axis
• Monoclinic one 2-fold axis
• Triclinic none

48. 48
Tetragonal symmetry Cubic symmetry
Cubic C = Tetragonal P Cubic F ≠≠≠≠ Tetragonal I

49. 49
The three Bravais lattices in the cubic crystal
system have the same rotational symmetry but
different translational symmetry.
Simple cubic
Primitive cubic
Cubic P
Body-centred cubic
Cubic I
Face-centred cubic
Cubic F

50. 50
QUESTIONS?

51. 51
Contents
Crystal, Lattice and Motif
Unit cells, Lattice Parameters and Projections
Miller Indices & Miller-Bravais Indices
Directions and Planes
Classification of Lattices:
7 crystal systems
14 Bravais lattices
Reciprocal lattice

52. 52
Miller Indices of directions and
planes
William Hallowes Miller
(1801 – 1880)
University of Cambridge
Miller Indices 1

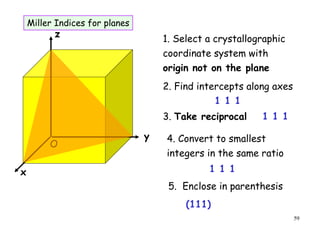
53. 53
1. Choose a point on the direction
as the origin.
2. Choose a coordinate system
with axes parallel to the unit
cell edges.
x
y 3. Find the coordinates of
another point on the direction in
terms of a, b and c
4. Reduce the coordinates to smallest integers.
5. Put in square brackets
Miller Indices of Directions
[100]
1a+0b+0c
z
1, 0, 0
1, 0, 0
Miller Indices 2
a
b
c

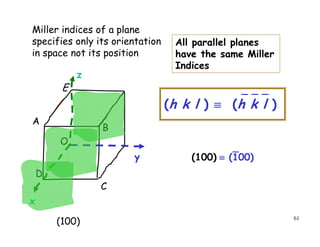
54. 54
y
z
Miller indices of a direction:
only the orientation
not its position or sense
All parallel directions have the
same Miller indices
[100]x
Miller Indices 3

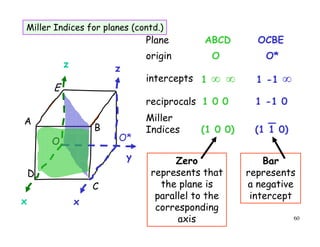
55. 55
x
y
z
O
A
1/2, 1/2, 1
[1 1 2]
OA=1/2 a + 1/2 b + 1 c
P
Q
x
y
z
PQ = -1 a -1 b + 1 c
-1, -1, 1
Miller Indices of
Directions (contd.)
[ 1 1 1 ]
__
-ve steps are shown as bar over the number
Direction OA
Direction PQ

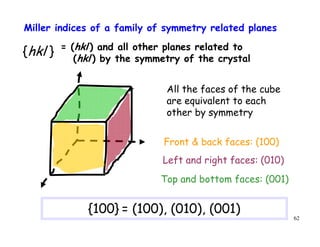
56. 56
Miller indices of a family of symmetry related directions
[100]
[001]
[010]
uvw = [uvw] and all other directions related to
[uvw] by the symmetry of the crystal
cubic
100 = [100], [010],
[001]
tetragonal
100 = [100], [010]
Cubic
Tetragonal
[010]
[100]
Miller Indices 4

57. 57
Slip System
A common microscopic mechanism of
plastic deformation involves slip on
some crystallographic planes known
as slip planes in certain
crystallographic directions called slip
directions.
A combination of slip direction lying
in a slip plane is called a slip system

58. 58
Miller indices of slip directions in CCP
y
z
[110]
[110]
[101]
[ 101]
[011]
[101]
Slip directions = close-packed directions = face diagonals
x
Six slip directions:
[110]
[101]
[011]
[110]
[101]
[101]
All six slip
directions in ccp:
110
Miller Indices 5

59. 59
5. Enclose in parenthesis
Miller Indices for planes
3. Take reciprocal
2. Find intercepts along axes
1. Select a crystallographic
coordinate system with
origin not on the plane
4. Convert to smallest
integers in the same ratio
1 1 1
1 1 1
1 1 1
(111)
x
y
z
O

60. 60
Miller Indices for planes (contd.)
origin
intercepts
reciprocals
Miller
Indices
A
B
C
D
O
ABCD
O
1 ∞ ∞
1 0 0
(1 0 0)
OCBE
O*
1 -1 ∞
1 -1 0
(1 1 0)
_
Plane
x
z
y
O*
x
z
E
Zero
represents that
the plane is
parallel to the
corresponding
axis
Bar
represents
a negative
intercept

61. 61
Miller indices of a plane
specifies only its orientation
in space not its position
All parallel planes
have the same Miller
Indices
A
B
C
D
O
x
z
y
E
(100)
(h k l ) ≡≡≡≡ (h k l )
_ _ _
(100) ≡≡≡≡ (100)
_

62. 62
Miller indices of a family of symmetry related planes
= (hkl ) and all other planes related to
(hkl ) by the symmetry of the crystal
{hkl }
All the faces of the cube
are equivalent to each
other by symmetry
Front & back faces: (100)
Left and right faces: (010)
Top and bottom faces: (001)
{100} = (100), (010), (001)

63. 63
Slip planes in a ccp crystal
Slip planes in ccp are the close-packed planes
AEG (111)
A
D
FE
D
G
x
y
z
B
C
y
ACE (111)
A
E
D
x
z
C
ACG (111)
A
G
x
y
z
C
A D
FE
D
G
x
y
z
B
C
All four slip
planes of a
ccp crystal:
{111}
D
E
G
x
y
z
C
CEG (111)

64. 64
{100}cubic = (100), (010), (001)
{100}tetragonal = (100), (010)
(001)
Cubic
Tetragonal
Miller indices of a family of
symmetry related planes
x
z
y
z
x
y

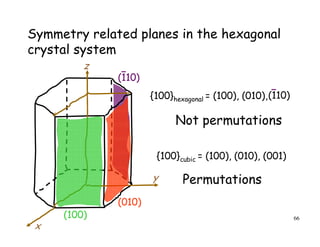
65. 65
[100]
[010]
Symmetry related directions in the
hexagonal crystal system
cubic
100 = [100], [010], [001]
hexagonal
100
Not permutations
Permutations
[110]
x
y
z
= [100], [010], [110]

66. 66
(010)
(100)
(110)
x
{100}hexagonal = (100), (010),
{100}cubic = (100), (010), (001)
Not permutations
Permutations
Symmetry related planes in the hexagonal
crystal system
(110)
y
z

67. 67
Problem:
In hexagonal system symmetry
related planes and directions do
NOT have Miller indices which
are permutations
Solution:
Use the four-index Miller-
Bravais Indices instead

68. 68
x1
x2
x3
(1010)
(0110)
(1100)
(hkl)=>(hkil) with i=-(h+k)
Introduce a fourth axis in
the basal plane
x1
x3
Miller-Bravais Indices of Planes
x2
Prismatic planes:
{1100} = (1100)
(1010)
(0110)
z

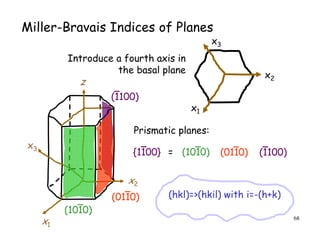
69. 69
Miller-Bravais Indices of Directions in
hexagonal crystals
x1
x2
x3
Basal plane
=slip plane
=(0001)
[uvw]=>[UVTW]
wWvuTuvVvuU =+−=−=−= );();2(
3
1
);2(
3
1
Require that: 0=++ TVU
Vectorially 0aaa 21 =++ 3
caa
caaa
wvu
WTVU
++=
+++
21
321
a1
a2
a2

70. 70
a1
a1
-a2
-a3
]0112[
a2
a3
x1
x2
x3
wWvuTuvVvuU =+−=−=−= );();2(
3
1
);2(
3
1
[ ] ]0112[0]100[ 3
1
3
1
3
2
≡−−⇒
[ ] ]0121[0]010[ 3
1
3
2
3
1
≡−−⇒
[ ] ]2011[0]011[ 3
2
3
1
3
1
≡−−⇒
x1:
x2:
x3:
Slip directions in hcp
0112
Miller-Bravais indices of slip directions in hcp
crystal:

71. 71
Some IMPORTANT Results
Condition for a direction [uvw] to be parallel to a plane or lie in
the plane (hkl):
h u + k v + l w = 0
Weiss zone law
True for ALL crystal systems
h U + k V + i T +l W = 0

72. 72
CUBIC CRYSTALS
[hkl] ⊥⊥⊥⊥ (hkl)
Angle between two directions [h1k1l1] and [h2k2l2]:
C
[111]
(111)
2
2
2
2
2
2
2
1
2
1
2
1
212121
cos
lkhlkh
llkkhh
++++
++
=θ

73. 73
dhkl
Interplanar spacing
between ‘successive’ (hkl)
planes passing through the
corners of the unit cell
222
lkh
acubic
hkld
++
=
O
x
(100)
ad =100
B
O
x
z
E
2011
a
d =

74. 74
[uvw] Miller indices of a direction (i.e. a set of
parallel directions)
<uvw> Miller indices of a family of symmetry
related directions
(hkl) Miller Indices of a plane (i.e. a set of
parallel planes)
{hkl} Miller indices of a family of symmetry
related planes
[uvtw] Miller-Bravais indices of a direction,
(hkil) plane in a hexagonal system
Summary of Notation convention for Indices

75. 75
Contents
Crystal, Lattice and Motif
Unit cells, Lattice Parameters and Projections
Miller Indices & Miller-Bravais Indices
Directions and Planes
Classification of Lattices:
7 crystal systems
14 Bravais lattices
Reciprocal lattice

76. 76
Reciprocal Lattice
A lattice can be defined in terms of three vectors
a, b and c along the edges of the unit cell
We now define another triplet of vectors a*, b*
and c* satisfying the following property:
The triplet a*, b* and c* define another unit cell
and thus a lattice called the reciprocal lattice.
The original lattice in relation to the reciprocal
lattice is called the direct lattice.
VVV
b)(a
c
a)(c
b
c)(b
a
×
=
×
=
×
= ∗∗∗
;;
V= volume of the unit cell

77. 77
Every crystal has a unique Direct Lattice and a
corresponding Reciprocal Lattice.
The reciprocal lattice vector ghkl has the
following interesting and useful properties:
A RECIPROCAL LATTICE VECTOR ghkl is a vector
with integer components h, k, l in the reciprocal
space:
∗∗∗
++= cbag lkhhkl
Reciprocal Lattice (contd.)

78. 78
hkl
hkl
d
1
=g
1. The reciprocal lattice vector ghkl with integer
components h, k, l is perpendicular to the
direct lattice plane with Miller indices (hkl):
)(hklhkl ⊥g
Properties of Reciprocal Lattice Vector:
2. The length of the reciprocal lattice vector
ghkl with integer components h, k, l is equal to
the reciprocal of the interplanar spacing of
direct lattice plane (hkl):

79. 79
Full significance of the
concept of the reciprocal
lattice will be appreciated
in the discussion of the x-
ray and electron
diffraction.

80. 80
Thank You

81. 81
Example:
Monatomic Body-Centred Cubic (BCC) crystal
e.g., Fe, Ti, Cr, W, Mo etc.
Atomic content of a unit cell:
fractional coordinates:
Fractional coordinates
of the two atoms
000; ½ ½ ½
Unit cell description : 8
Effective no. of atoms in
the unit cell
218
8
1
=+×
corners Body
centre
000
½ ½ ½