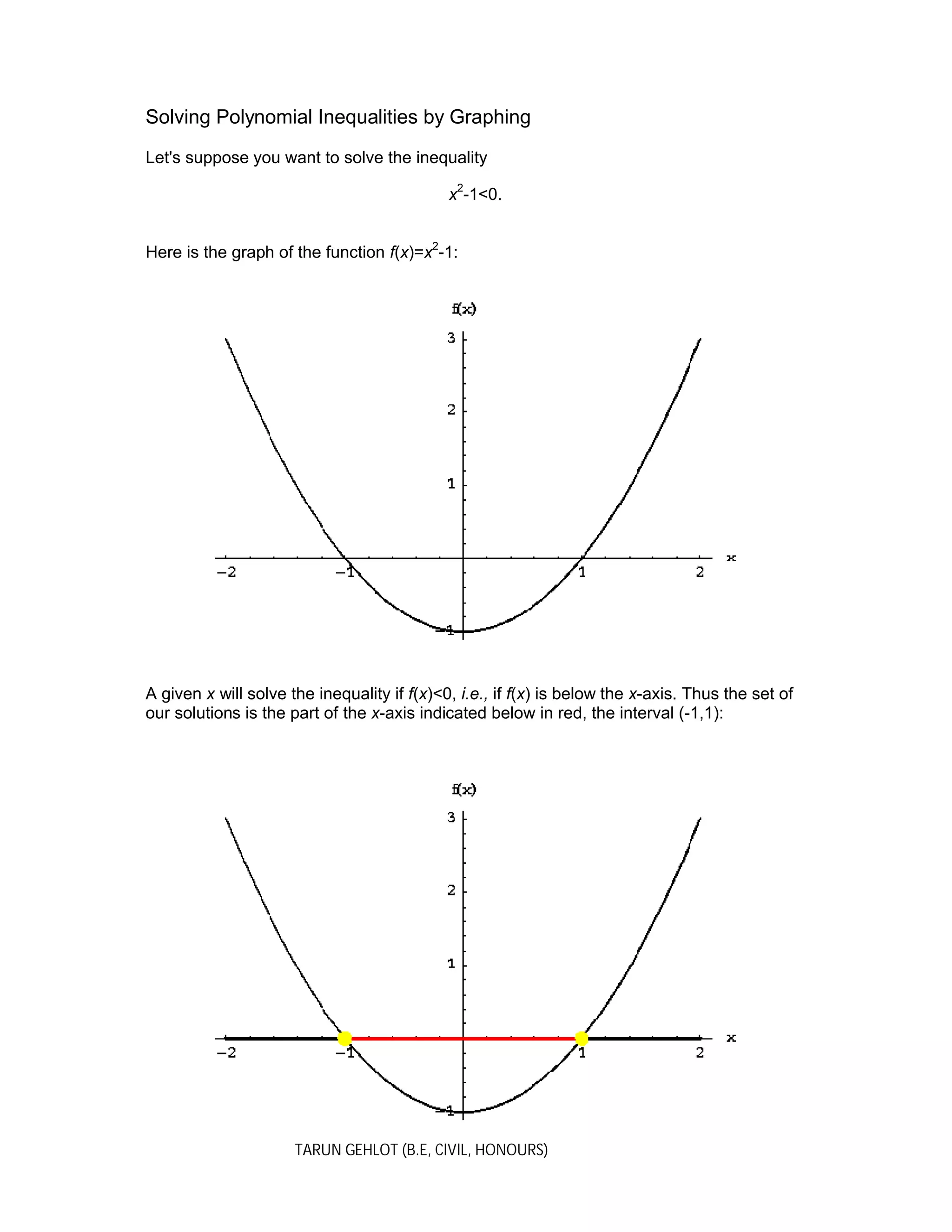
This document discusses solving polynomial inequalities by graphing. It explains that the solutions to an inequality like x^2 - 1 < 0 are the x-values where the graph of f(x)=x^2 - 1 is below the x-axis, or the interval (-1,1). Similarly, the solutions to x^2 - 1 > 0 are where the graph is above the x-axis. The x-intercepts, where f(x)=0, separate parts of the graph above and below the x-axis. Another example solves the inequality x^4 + x^3 - 2x^2 - 2x > 0, whose solutions are the union of the intervals (-1,0), (

1. TARUN GEHLOT (B.E, CIVIL, HONOURS)
Solving Polynomial Inequalities by Graphing
Let's suppose you want to solve the inequality
x2
-1<0.
Here is the graph of the function f(x)=x2
-1:
A given x will solve the inequality if f(x)<0, i.e., if f(x) is below the x-axis. Thus the set of
our solutions is the part of the x-axis indicated below in red, the interval (-1,1):

2. TARUN GEHLOT (B.E, CIVIL, HONOURS)
If we want to see the solutions of the inequality
x2
-1>0,
that's just as easy. Now we have to pick all values of x for which f(x)=x2
-1 is above the x-
axis. As you can see, we obtain as solutions the set , indicated
below in blue.
Note the pivotal role played by the "yellow dots", the x-intercepts of f(x).
f(x) can only change its sign by passing through an x-intercept, i.e., a solution of f(x)=0
will always separate parts of the graph of f(x) above the x-axis from parts below the x-
axis. This property of polynomials is called theIntermediate Value Property of
polynomials; your teacher might also refer to this property as continuity.
Let us consider another example: Solve the inequality
Here is the graph of the function f(x)=x4
+x3
-2x2
-2x>0:

3. TARUN GEHLOT (B.E, CIVIL, HONOURS)
A given x will solve the inequality if , i.e., if f(x) is above the x-axis. Thus the
set of our solutions is the part of the x-axis indicated below in blue, the union of the
following three intervals:

4. TARUN GEHLOT (B.E, CIVIL, HONOURS)
The (finite) endpoints are included since at these points f(x)=0 and so these x's are
included in our quest of finding the solutions of .
Our answer is approximate, the endpoints of the intervals were found by inspection; you
can usually obtain better estimates for the endpoints by using a numerical solver to find
the solutions of f(x)=0. In fact, as you will learn in the next section, the precise endpoints
of the intervals are , -1, 0 and .
Two more caveats: The method will only work, if your graphing window contains all x-
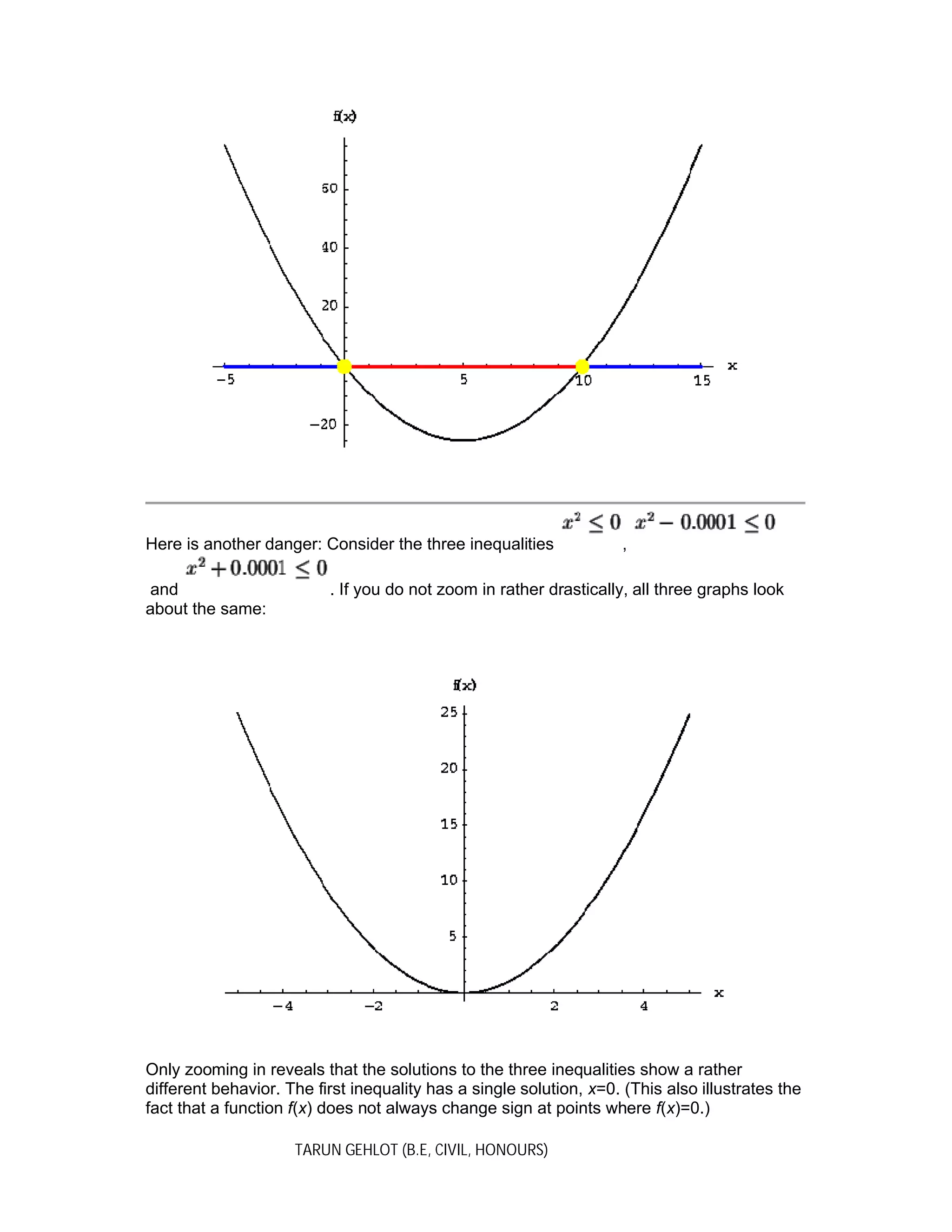
intercepts. Here is a rather simple-minded example to illustrate the point: Suppose you
want to solve the inequality
x2
-10x<0.
If your graphing window is set to the interval [-5,5], you will miss half of the action, and
probably come up with the incorrect answer:
To find the correct answer, the interval (0,10), your graphing window has to include the
second x-intercept at x=10:

5. TARUN GEHLOT (B.E, CIVIL, HONOURS)
Here is another danger: Consider the three inequalities ,
and . If you do not zoom in rather drastically, all three graphs look
about the same:
Only zooming in reveals that the solutions to the three inequalities show a rather
different behavior. The first inequality has a single solution, x=0. (This also illustrates the
fact that a function f(x) does not always change sign at points where f(x)=0.)

6. TARUN GEHLOT (B.E, CIVIL, HONOURS)
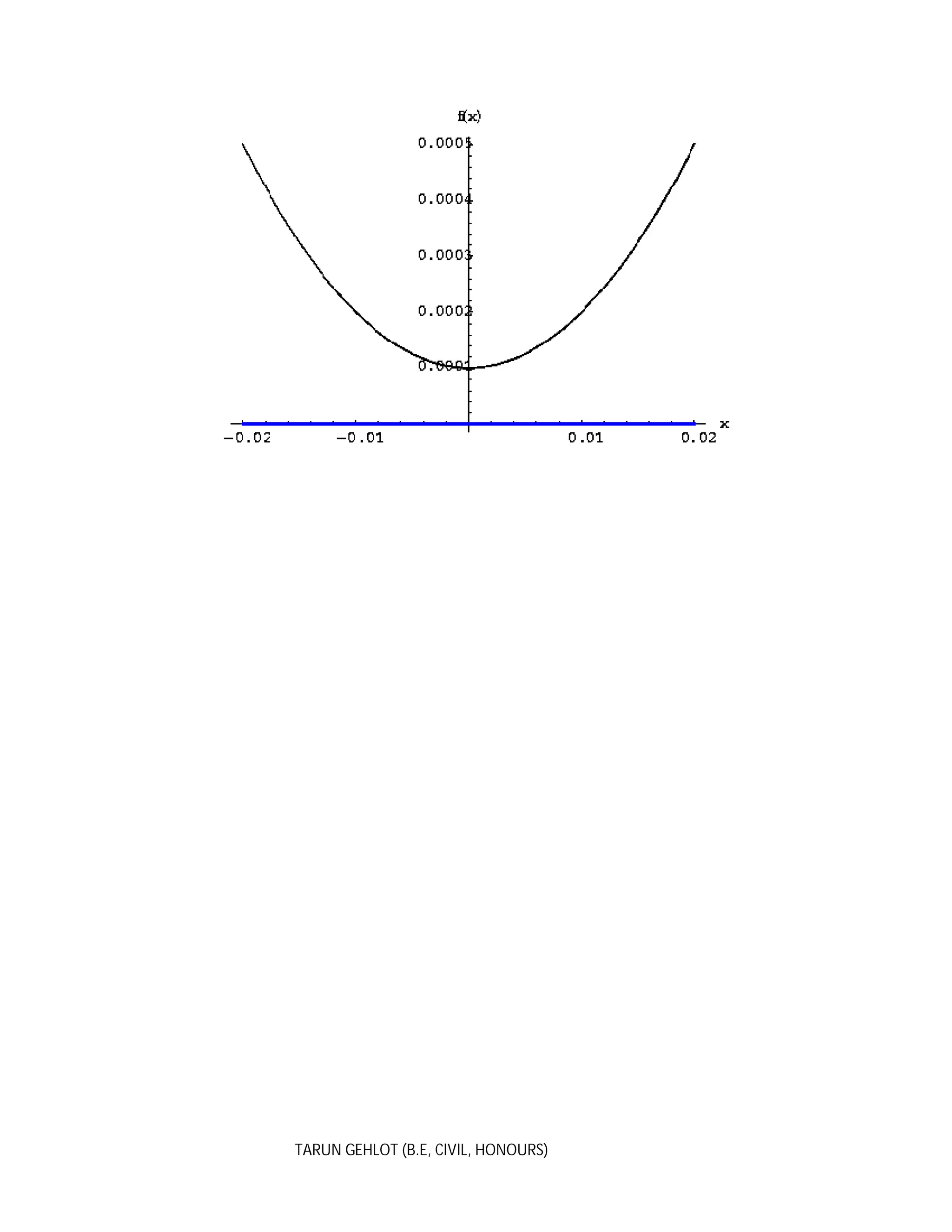
The second inequality, , has as its solutions the interval [-0.01,0.01]:
The third inequality, , has no solutions:

7. TARUN GEHLOT (B.E, CIVIL, HONOURS)