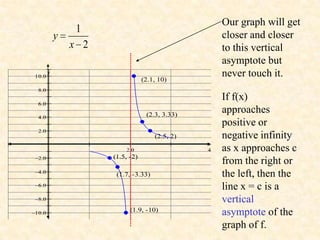
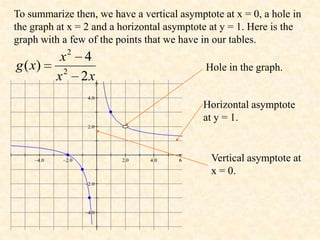
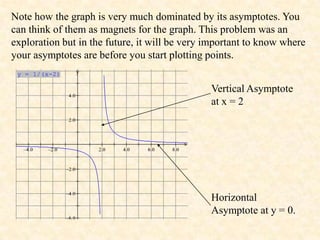
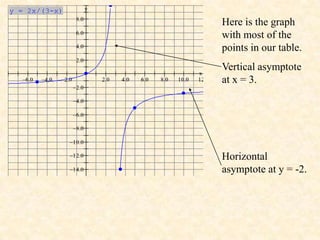
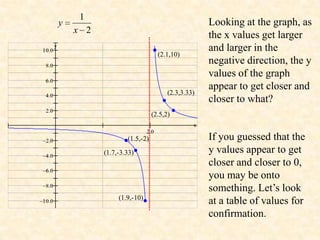
1. The rational function f(x) = 1/x^2 has a vertical asymptote at x = 2 because the denominator is 0 at that point. 2. As x values approach 2 from either side, y values approach positive or negative infinity, respectively. 3. The graph gets closer and closer to the vertical line x = 2 but never touches it. This line is called a vertical asymptote. 4. The graph also has a horizontal asymptote at y = 0, as y values approach 0 as x values increase or decrease indefinitely.

1. Graphs of Rational Functions

2. A rational function is a function that can be expressed in the form
f ( x)
y where both f(x) and g(x) are polynomial functions.
g ( x)
Examples of rational functions would be:
1
y
x 2
2x
f ( x)
3 x
x2 4
g ( x)
x2 2x
Over the next few frames we will look at the graphs of each of
the above functions.

3. 1
First we will look at y .
x 2
This function has one value of x that is banned from the domain.
What value of x do you think that would be? And why?
If you guessed x = 2, congratulations. This is the value at which
the function is undefined because x = 2 generates 0 in the
denominator.
Consider the graph of the function. What impact do you
think this forbidden point will have on the graph?
Think before you click.

4. Now just because we cannot use x = 2 in our x-y table, it does not
mean that we cannot use values of x that are close to 2. So before
you click again, fill in the values in the table below.
1
x y
x 2
As we pick values of x that are smaller
1.5 -2
than 2 but closer and closer to 2 what do
1.7 -3.33 you think is happening to y?
1.9 -10
2.0 undefined If you said that y is getting closer and
closer to negative infinity, nice job!

5. Now fill in the values in the rest of the table.
1
x y What about the behavior of the function
x 2
on the other side of x = 2? As we pick
1.5 -2
values of x that are larger than 2 but closer
1.7 -3.33 and closer to 2 what do you think is
happening to y?
1.9 -10
2.0 Und If you said that y is getting closer and
10 closer to positive infinity, you are right
2.1
on the money!
2.3 3.33
2.5 2

6. Let’s see what the points that we have calculated so far would look
like on graph.
1
y
x 2 This dotted
vertical line is a
y
(2.1, 10) crucial visual aid
for the graph. Do
you know what
(2.3, 3.33) the equation of
(2.5, 2)
this dotted line is?
x
(1.5, -2) The equation is
(1.7, -3.33) x = 2 because
every point on
the line has an
(1.9, -10) x coordinate of
2.

7. 1 Do you know
y
x 2 what this dotted
y vertical line is
(2.1, 10)
called?
(2.3, 3.33) Hint: it is one of
the many great
(2.5, 2)
x
and imaginative
(1.5, -2)
words in
mathematics.
(1.7, -3.33)
The line x = 2 is a
vertical asymptote.
(1.9, -10)

8. Our graph will get
1
y closer and closer
x 2 to this vertical
asymptote but
y
(2.1, 10)
never touch it.
If f(x)
(2.3, 3.33)
approaches
positive or
(2.5, 2) negative infinity
x
as x approaches c
(1.5, -2)
from the right or
(1.7, -3.33) the left, then the
line x = c is a
vertical
(1.9, -10)
asymptote of the
graph of f.

9. A horizontal asymptote is a horizontal line that the graph gets
closer and closer to but never touches. The official definition of a
horizontal asymptote:
The line y = c is a horizontal asymptote for the graph of a
function f if f(x) approaches c as x approaches positive or
negative infinity.
Huh?!
Don’t you just love official definitions? At any rate,
rational functions have a tendency to generate
asymptotes, so lets go back to the graph and see if we can
find a horizontal asymptote.

10. 1
y Looking at the graph, as
x 2
the x values get larger
y
and larger in the
(2.1,10)
negative direction, the y
values of the graph
appear to get closer and
(2.3,3.33)
closer to what?
(2.5,2)
x
(1.5,-2) If you guessed that the
(1.7,-3.33) y values appear to get
closer and closer to 0,
you may be onto
something. Let’s look
(1.9,-10)
at a table of values for
confirmation.

11. Before you click again, take a minute to calculate the y values in
the table below. What is your conclusion about the trend?
1
x y
x 2
0 -(1/2)
-5 -(1/7)
-20 -(1/22)
-100 -(1/102)
Conclusion: as the x values get closer and closer to negative
infinity, the y values will get closer and closer to 0.
Question: will the same thing happen as x values get closer to
positive infinity?

12. How about a guess? What do you think is going to happen to the y
values of our function as the x values get closer to positive infinity?
1
As x , y ?
x 2
1
As x , y 0
x 2
By looking at the fraction analytically, you can hopefully see that
very large values of x will generate values of y very close to 0. If
you are uneasy about this, expand the table in the previous slide to
include values like x = 10, 100, or 1000.
On the next frame then, is our final graph for this problem

13. Note how the graph is very much dominated by its asymptotes. You
can think of them as magnets for the graph. This problem was an
exploration but in the future, it will be very important to know where
your asymptotes are before you start plotting points.
y = 1/(x-2) y
Vertical Asymptote
at x = 2
x
Horizontal
Asymptote at y = 0.

14. Next up is the graph of one of the functions that was mentioned
back in frame #2.
2x
f ( x)
3 x
Let’s see if we can pick out the asymptotes analytically before we
start plotting points in an x-y table.
Do we have a vertical asymptote? If so, at what value of x?
We have a vertical asymptote at x = 3 because at that value of x, the
denominator is 0 but the numerator is not. Congratulations if you
picked this out on your own.
The horizontal asymptote is a little more challenging, but go ahead
and take a guess.

15. Notice though that as values of x get larger and larger, the 3 in the
denominator carries less and less weight in the calculation.
2x
f ( x) As the 3 “disappears”, the function looks
3 x
more and more like…
2x
f ( x)
x which reduces to y = -2.
This means that we should have a horizontal asymptote at y = -2.
We already have evidence of a vertical asymptote at x = 3. So we
are going to set up the x-y table then with a few values to the left
of x = 3 and a few values to the right of x = 3. To confirm the
horizontal asymptote we will also use a few large values of x just
to see if the corresponding values of y will be close to y = -2.

16. 2x
x y Take a few minutes and work out the
3 x y values for this table.
-5 -10/8 = -1.25
0 0 Don’t be lazy now, work them out
2.5 5/.5 = 10 yourself.
3 Undefined
As expected, y values tend to explode
3.5 7/-.5 = -14 when they get close to the vertical
5 10/-2 = -5 asymptote at x = 3.
10 20/-7 = -2.86 Also, as x values get large, y values
get closer and closer to the horizontal
50 100/-47= -2.13 asymptote at y = -2.
The graph is a click away.

17. y = 2x/(3-x) y
Here is the graph
with most of the
points in our table.
x
Vertical asymptote
at x = 3.
Horizontal
asymptote at y = -2.

18. Believe it or not, you are now sophisticated enough mathematically
to draw conclusions about the graph three ways:
Analytically: Numerically: Graphically: a
finding supporting and visual look at the
asymptotes with generating behavior of the
algebra!! conclusions function.
with the x-y
table!!
If your conclusions from the above areas do not agree, investigate
further to uncover the nature of the problem.

19. We are going to finish this lesson with an analysis of the third
function that was mentioned in the very beginning:
2
x 4
g ( x) 2
This is a rational function so we have
x 2x potential for asymptotes and this is
what we should investigate first. Take
a minute to form your own opinion
before you continue.
Hopefully you began by setting the denominator equal to 0.
It appears that we may have vertical
x2 2x 0 asymptotes at x = 0 and at x = 2. We will
xx 2 0 see if the table confirms this suspicion.
x 0, x 2

20. x2 4 See anything peculiar?
x y
x2 2x Notice that as x values get closer and
-2 0 closer to 0, the y values get larger and
larger. This is appropriate behavior
-1 -1
near an asymptote.
-.5 -3
But as x values get closer and closer
-.1 -19 to 2, the y values do not get large. In
fact, the y values seem to get closer
0 Und
and closer to 2.
1 3
Now, if x =2 creates 0 in the
1.5 2.33 denominator why don’t we have an
1.9 2.05 asymptote at x = 2?
2 und

21. We don’t get a vertical asymptote at x = 2
because when x = 2 both the numerator and
the denominator are equal to 0. In fact, if we
had thought to reduce the function in the
beginning, we could have saved ourselves a lot
of trouble. Check this out:
x2 4 x 2 x 2 x 2
y
x2 2x xx 2 x
x2 4 x 2
Does this mean that y and y
x2 2x x
are identical functions?
Yes, at every value of x except x = 2 where the former is undefined.
There will be a tiny hole in the graph where x = 2.

22. 2 As we look for horizontal asymptotes, we
x 4
g ( x) 2
look at y values as x approaches plus or
x 2x minus infinity. The denominator will get
very large but so will the numerator.
As was the case with
the previous function, You can verify this in the table.
we concentrate on the
ratio of the term with x2 4
the largest power of x
x y
in the numerator to
x2 2x
the term with the 10 1.2
largest power of x in
the denominator. As x 100 1.02
gets large… 1000 1.002
2 2
x 4 x So, we have a horizontal asymptote at
2 2
1
x 2x x y = 1.

23. To summarize then, we have a vertical asymptote at x = 0, a hole in
the graph at x = 2 and a horizontal asymptote at y = 1. Here is the
graph with a few of the points that we have in our tables.
2
x 4
g ( x) 2 Hole in the graph.
x 2x y
Horizontal asymptote
at y = 1.
x
Vertical asymptote at
x = 0.

24. Steps to graph when x is not to the 1st power
1. Find the x-intercepts. (Set numer. =0 and solve)
2. Find vertical asymptote(s). (set denom=0 and solve)
3. Find horizontal asymptote. 3 cases:
a. If degree of top < degree of bottom, y=0
lead. coeff. of top
b. If degrees are =, y
lead. coeff. of bottom
c. If degree of top > degree of bottom, no horiz. asymp,
but there will be a slant asymptote.
4. Make a T-chart: choose x-values on either side &
between all vertical asymptotes.
5. Graph asymptotes, pts., and connect with curves.
6. Check solutions on calculator.

25. Now you will get a chance to practice on exercises that use the
topics that were covered in this lesson:
Finding vertical and horizontal asymptotes in rational functions.
Graphing rational functions with asymptotes.
Good luck and watch out for those asymptotes!

26. Now you try!
• Pg 489 #’s 16, 18, 20, 22