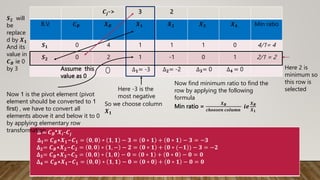
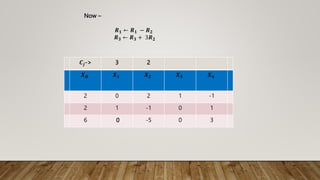
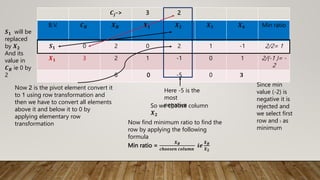
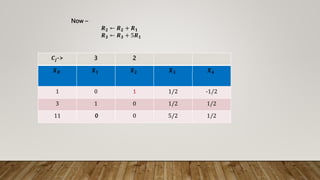
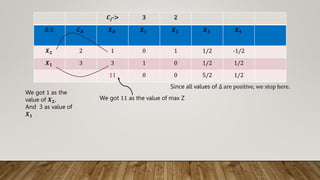
The document details the simplex method applied to a linear programming problem with the objective of maximizing the function z = 3x1 + 2x2 under specific constraints. It outlines the steps involved in incorporating slack variables, performing row transformations, and identifying pivot elements to arrive at the optimal solution. The final result indicates that the maximum value of z is 11, achieved with x1 = 3 and x2 = 1.

1. SIMPLEX METHOD
BY - ABHISHEK DUTTA

2. Q – CONSIDER THE LPP -
• max Z = 3𝑥1 +2𝑥2 𝑠𝑢𝑏𝑗𝑒𝑐𝑡 𝑡𝑜 𝑐𝑜𝑛𝑠𝑡𝑟𝑎𝑖𝑛𝑡𝑠 −
• 𝒙𝟏 +𝒙𝟐 ≤ 4
• 𝒙𝟏 - 𝒙𝟐 ≤ 2
• 𝒙𝟏, 𝒙𝟐 ≥ 0
• Now
• 𝒙𝟏 +𝒙𝟐 ≤ 4 --adding slack variable 𝒙𝟏 +𝒙𝟐 + 𝒙𝟑 = 4
• 𝒙𝟏 - 𝒙𝟐 ≤ 2 --adding slack variable 𝒙𝟏 - 𝒙𝟐 + 𝒙𝟒 = 2
• 𝒙𝟏, 𝒙𝟐 ≥ 0

3. 𝑪𝒋-> 3 2
B.V. 𝑪𝑩 𝑿𝑩 𝑿𝟏 𝑿𝟐 𝑿𝟑 𝑿𝟒 Min ratio
𝑺𝟏 0 4 1 1 1 0
𝑺𝟐 0 2 1 -1 0 1
(𝟏)𝒙𝟏 +(𝟏)𝒙𝟐 + 𝟏 𝒙𝟑+ 𝟎 𝒙𝟒= 4
(𝟏)𝒙𝟏 +(−𝟏)𝒙𝟐 + 𝟎 𝒙𝟑+ (𝟏)𝒙𝟒= 2
𝒙𝟏, 𝒙𝟐 ≥ 0

4. 𝑪𝒋-> 3 2
B.V. 𝑪𝑩 𝑿𝑩 𝑿𝟏 𝑿𝟐 𝑿𝟑 𝑿𝟒 Min ratio
𝑺𝟏 0 4 1 1 1 0 4/1= 4
𝑺𝟐 0 2 1 -1 0 1 2/1 = 2
∆𝟏= -3 ∆𝟐= -2 ∆𝟑= 0 ∆𝟒 = 0
∆ = 𝑪𝑩*𝑿𝒊-𝑪𝒋
∆𝟏= 𝑪𝑩∗𝑿𝟏−𝑪𝟏 = 𝟎, 𝟎 ∗ 𝟏, 𝟏 − 𝟑 = 𝟎 ∗ 𝟏 + 𝟎 ∗ 𝟏 − 𝟑 = −𝟑
∆𝟐= 𝑪𝑩∗𝑿𝟐−𝑪𝟐 = 𝟎, 𝟎 ∗ 𝟏, − − 𝟐 = 𝟎 ∗ 𝟏 + 𝟎 ∗ (−𝟏 ) − 𝟑 = −𝟐
∆𝟑= 𝑪𝑩∗𝑿𝟑−𝑪𝟑 = 𝟎, 𝟎 ∗ 𝟏, 𝟎 − 𝟎 = 𝟎 ∗ 𝟏 + 𝟎 ∗ 𝟎 − 𝟎 = 𝟎
∆𝟒 = 𝑪𝑩∗𝑿𝟏−𝑪𝟏 = 𝟎, 𝟎 ∗ 𝟏, 𝟏 − 𝟎 = 𝟎 ∗ 𝟎 + 𝟎 ∗ 𝟏 − 𝟎 = 𝟎
Here -3 is the
most negative
So we choose column
𝑿𝟏
Now find minimum ratio to find the
row by applying the following
formula
Min ratio =
𝑿𝑩
𝒄𝒉𝒐𝒐𝒔𝒆𝒏 𝒄𝒐𝒍𝒖𝒎𝒏
𝒊𝒆
𝑿𝑩
𝑿𝟏
Here 2 is
minimum so
this row is
selected
Now 1 is the pivot element (pivot
element should be converted to 1
first) , we have to convert all
elements above it and below it to 0
by applying elementary row
transformation
𝑺𝟐 will
be
replace
d by 𝑿𝟏
And its
value in
𝑪𝑩 ie 0
by 3 Assume this
value as 0

5. 𝑪𝒋-> 3 2
𝑿𝑩 𝑿𝟏 𝑿𝟐 𝑿𝟑 𝑿𝟒
2 0 2 1 -1
2 1 -1 0 1
6 0 -5 0 3
Now –
𝑹𝟏 ← 𝑹𝟏 − 𝑹𝟐
𝑹𝟑 ← 𝑹𝟑 + 3𝑹𝟐

6. 𝑪𝒋-> 3 2
B.V. 𝑪𝑩 𝑿𝑩 𝑿𝟏 𝑿𝟐 𝑿𝟑 𝑿𝟒 Min ratio
𝑺𝟏 0 2 0 2 1 -1 2/2= 1
𝑿𝟏 3 2 1 -1 0 1 2/(-1 )= -
2
6 0 -5 0 𝟑
Here -5 is the
most
negative
So we choose column
𝑿𝟐
Now find minimum ratio to find the
row by applying the following
formula
Min ratio =
𝑿𝑩
𝒄𝒉𝒐𝒐𝒔𝒆𝒏 𝒄𝒐𝒍𝒖𝒎𝒏
𝒊𝒆
𝑿𝑩
𝑿𝟐
Since min
value (-2) is
negative it is
rejected and
we select first
row and 1 as
minimum
𝑺𝟏 will be
replaced
by 𝑿𝟐
And its
value in
𝑪𝑩 ie 0 by
2
Now 2 is the pivot element convert it
to 1 using row transformation and
then we have to convert all elements
above it and below it to 0 by
applying elementary row
transformation

7. 𝑪𝒋-> 3 2
𝑿𝑩 𝑿𝟏 𝑿𝟐 𝑿𝟑 𝑿𝟒
1 0 1 1/2 -1/2
2 1 -1 0 1
6 0 -5 0 3
Now –
𝑹𝟏 ← 𝑹𝟏 ∗ (
𝟏
𝟐
)

8. Now –
𝑹𝟐 ← 𝑹𝟐 + 𝑹𝟏
𝑹𝟑 ← 𝑹𝟑 + 5𝑹𝟏
𝑪𝒋-> 3 2
𝑿𝑩 𝑿𝟏 𝑿𝟐 𝑿𝟑 𝑿𝟒
1 0 1 1/2 -1/2
3 1 0 1/2 1/2
11 0 0 5/2 1/2

9. 𝑪𝒋-> 3 2
B.V. 𝑪𝑩 𝑿𝑩 𝑿𝟏 𝑿𝟐 𝑿𝟑 𝑿𝟒
𝑿𝟐 2 1 0 1 1/2 -1/2
𝑿𝟏 3 3 1 0 1/2 1/2
11 0 0 5/2 1/2
Since all values of ∆ are positive, we stop here.
We got 11 as the value of max Z
We got 1 as the
value of 𝑿𝟐,
And 3 as value of
𝑿𝟏

10. 𝑿𝟐 = 1
𝑿𝟏 = 3
max Z = 3𝑥1 +2𝑥2
Putting value of 𝑥1 and 𝑥2
max Z = 3(3)+2(1)
= 9+2
= 11