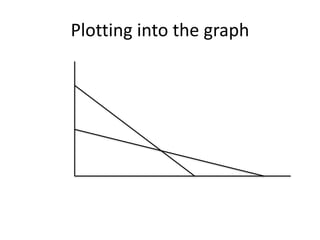
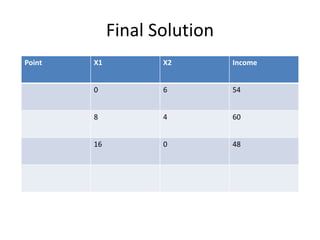
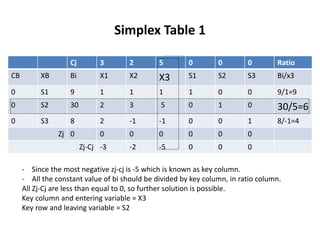
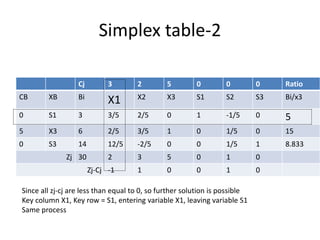
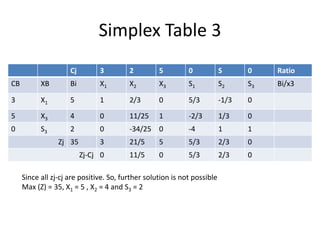
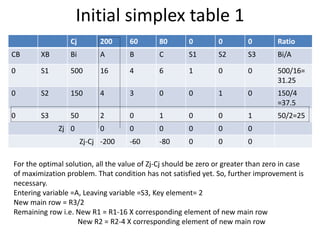
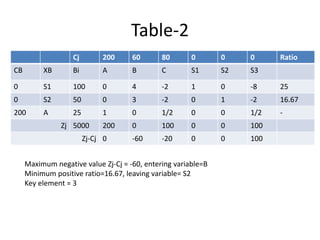
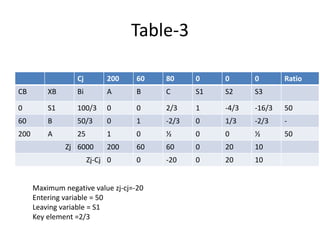
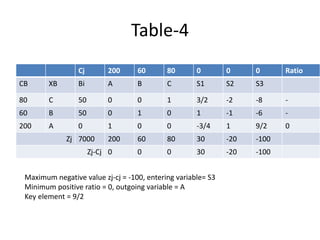
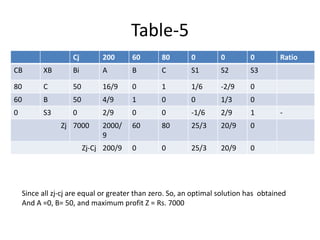
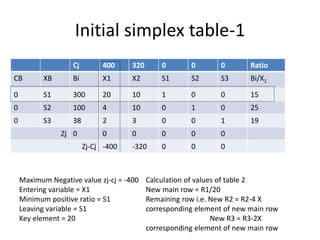
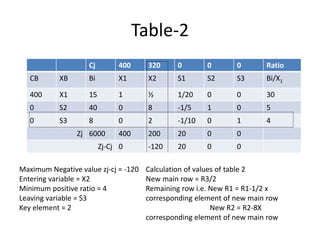
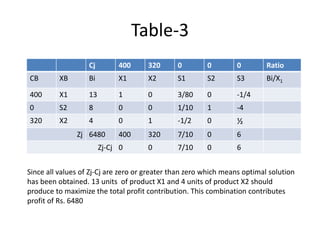
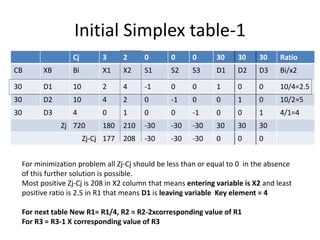
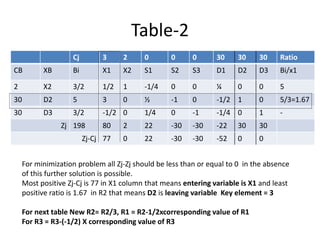
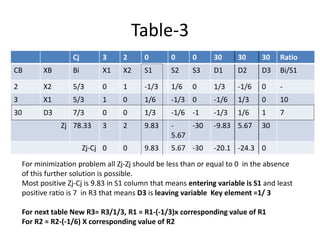
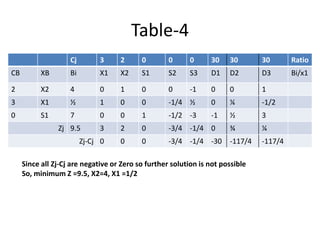
This document discusses linear programming and provides examples of how to solve linear programming problems graphically and using the simplex method. It introduces linear programming as a technique to allocate limited resources to find the best possible solution. The graphical method and simplex method are presented as two approaches to solve linear programming problems. An example problem is solved step-by-step using the graphical method and another is solved using the simplex method.

1. Linear Programming
By : Raju Raut

2. Introduction
• Linear programming is a mathematical
technique in computer modeling to find the
best possible solution in allocating limited
resources.

3. Methods
• Graphical Method
• Simplex Method

4. Graphical Method
• Example
Objective Function :
Maximize Z = 3X1 + 9X2
S.T.C
X1+4X2 ≤ 24
X1 +2X2 ≤ 16
Required : Formulate the problem graphically

5. Solution
• Converting the equation into equality
X1 + 4X2 = 24 ……………………………(1)
X1 + 2X2 = 16 …………………………….(2)
From Eq 1, when X1 = 0,
0 + 4X2 = 24
X2 = 24/4
= 6
(0, 6)

6. Con…
Similarly,
When X2 = 0
X1 + 4 X 0 = 24
X1 = 24
(24, 0)
Similarly from eq (2)
When X1 = 0, X2 = 8 (0,8)
X2 = 0, X1 = 16 (16, 0)

7. Plotting into the graph

8. Final Solution
Point X1 X2 Income
0 6 54
8 4 60
16 0 48

9. Simplex Method
• Algebraic method is not suitable for large
solution. So, we use simplex method
Maximization case
Max z = 6x1 + 4x2
S.T.C.
2X1+3X2 ≤ 120 ………………….(1)
2X1+X2 ≤ 60………………………(2)
Where, x1, x2 ≥ 0

10. Cont…
Max Z = 6x1 + 4x2 + 0s1+0s2
S.T.C.
2x1 + 3x2 +S1 = 120
2x1 + x2 + S2 = 60
S1 = slack variable
(note : in the case of ≤ we have to introduce
slack variable s1 and s2)

11. Ex.
Solve the following problem using simplex method
Maximize (z) = 3X1+2X2+5X3
S.T.C
X1+X2+X3≤9
2X1+3X2+5X3 ≤30
2X1-X2-X3≤8
Where, x1, x2,x3 ≥0

12. Solution
Converting inequalities to equalities after adding
slack variable
Maximize (Z) = 3X1+2X2+5X3+0S1+0S2+0S3
Subject to constraint
X1+x2+x3+s1=9
2x1+3x2+5x3 +s2=30
2x1-x2-x3+s3=8

13. Simplex Table 1
Cj 3 2 5 0 0 0 Ratio
CB XB Bi X1 X2 X3 S1 S2 S3 Bi/x3
0 S1 9 1 1 1 1 0 0 9/1=9
0 S2 30 2 3 5 0 1 0 30/5=6
0 S3 8 2 -1 -1 0 0 1 8/-1=4
Zj 0 0 0 0 0 0 0
Zj-Cj -3 -2 -5 0 0 0
- Since the most negative zj-cj is -5 which is known as key column.
- All the constant value of bi should be divided by key column, in ratio column.
All Zj-Cj are less than equal to 0, so further solution is possible.
Key column and entering variable = X3
Key row and leaving variable = S2

14. Calculation the value for table 2
• Calculation of key row
Key row = Element in key row
Intersectional element in key row
R2 = 30/5= 6, 2/5, 3/5, 5/5, 0/5=0, 1/5, 0/5=0
Remaining row= Element in old row-intersectional element in
old row x corresponding element in main row
R1= 9 – 1 x 6=3, 1-1x2/5 =3/5, 1-1x3/5=2/5
1-1x1=0, 1-1x0=1, 0-1 x 1/5=-1/5, 0-1 x 0=0

15. Calculation
• R3 = 8-(-1)x6=14,
2 -(-1) x 2/5 =12/5
-1 -(-1) x 3/5 =-2/5
-1 -(-1) x1 =0
0 -(-1) x0 =0
0 -(-1) x1/5 =1/5
1 -(-1) x0 =1

16. Simplex table-2
Cj 3 2 5 0 0 0 Ratio
CB XB Bi
X1 X2 X3 S1 S2 S3 Bi/x3
0 S1 3 3/5 2/5 0 1 -1/5 0 5
5 X3 6 2/5 3/5 1 0 1/5 0 15
0 S3 14 12/5 -2/5 0 0 1/5 1 8.833
Zj 30 2 3 5 0 1 0
Zj-Cj -1 1 0 0 1 0
Since all zj-cj are less than equal to 0, so further solution is possible
Key column X1, Key row = S1, entering variable X1, leaving variable S1
Same process

17. Simplex Table 3
Cj 3 2 5 0 S 0 Ratio
CB XB Bi X1 X2 X3 S1 S2 S3 Bi/x3
3 X1 5 1 2/3 0 5/3 -1/3 0
5 X3 4 0 11/25 1 -2/3 1/3 0
0 S3 2 0 -34/25 0 -4 1 1
Zj 35 3 21/5 5 5/3 2/3 0
Zj-Cj 0 11/5 0 5/3 2/3 0
Since all zj-cj are positive. So, further solution is not possible
Max (Z) = 35, X1 = 5 , X2 = 4 and S3 = 2

18. Ex :-2
Max Z = 200A +60B +80C
S.T.C.
16A+4B+6C ≤500
4A+3B+0C ≤150
2A+0B+C ≤ 50
A,B,C ≥0

19. Solution
We need to convert inequalities of the constraints to
equalities to solve LPP problem. So, we introduce slack
variables S1,S2 and S3 to the above three constraints
equations respectively. Then the problem will be as
below :
Maximize Z =200A +60B + 80C +OS1 +OS2 +0S3
Subject to constraints :
16A+4B+6C +S1 = 500
4A+3B+0C +S2=150
2A+0B+C +S3=50
And A, B, C, S1,S2 and S3 ≥ 0

20. Initial simplex table 1
Cj 200 60 80 0 0 0 Ratio
CB XB Bi A B C S1 S2 S3 Bi/A
0 S1 500 16 4 6 1 0 0 500/16=
31.25
0 S2 150 4 3 0 0 1 0 150/4
=37.5
0 S3 50 2 0 1 0 0 1 50/2=25
Zj 0 0 0 0 0 0 0
Zj-Cj -200 -60 -80 0 0 0
For the optimal solution, all the value of Zj-Cj should be zero or greater than zero in case
of maximization problem. That condition has not satisfied yet. So, further improvement is
necessary.
Entering variable =A, Leaving variable =S3, Key element= 2
New main row = R3/2
Remaining row i.e. New R1 = R1-16 X corresponding element of new main row
New R2 = R2-4 X corresponding element of new main row

21. Table-2
Cj 200 60 80 0 0 0 Ratio
CB XB Bi A B C S1 S2 S3
0 S1 100 0 4 -2 1 0 -8 25
0 S2 50 0 3 -2 0 1 -2 16.67
200 A 25 1 0 1/2 0 0 1/2 -
Zj 5000 200 0 100 0 0 100
Zj-Cj 0 -60 -20 0 0 100
Maximum negative value Zj-Cj = -60, entering variable=B
Minimum positive ratio=16.67, leaving variable= S2
Key element = 3

22. Table-3
Cj 200 60 80 0 0 0 Ratio
CB XB Bi A B C S1 S2 S3
0 S1 100/3 0 0 2/3 1 -4/3 -16/3 50
60 B 50/3 0 1 -2/3 0 1/3 -2/3 -
200 A 25 1 0 ½ 0 0 ½ 50
Zj 6000 200 60 60 0 20 10
Zj-Cj 0 0 -20 0 20 10
Maximum negative value zj-cj=-20
Entering variable = 50
Leaving variable = S1
Key element =2/3

23. Table-4
Cj 200 60 80 0 0 0 Ratio
CB XB Bi A B C S1 S2 S3
80 C 50 0 0 1 3/2 -2 -8 -
60 B 50 0 1 0 1 -1 -6 -
200 A 0 1 0 0 -3/4 1 9/2 0
Zj 7000 200 60 80 30 -20 -100
Zj-Cj 0 0 0 30 -20 -100
Maximum negative value zj-cj = -100, entering variable= S3
Minimum positive ratio = 0, outgoing variable = A
Key element = 9/2

24. Table-5
Cj 200 60 80 0 0 0 Ratio
CB XB Bi A B C S1 S2 S3
80 C 50 16/9 0 1 1/6 -2/9 0
60 B 50 4/9 1 0 0 1/3 0
0 S3 0 2/9 0 0 -1/6 2/9 1 -
Zj 7000 2000/
9
60 80 25/3 20/9 0
Zj-Cj 200/9 0 0 25/3 20/9 0
Since all zj-cj are equal or greater than zero. So, an optimal solution has obtained
And A =0, B= 50, and maximum profit Z = Rs. 7000

25. Ex
Max Z = 400X1+ 320X2
S.T.C.
20X1+10X2 ≤300
4X1+10X2 ≤100
2X1+3X2 ≤38

26. Solution
• Objective function
Max Z = 400X1 + 320X2 + 0S1 + 0S2 +0S3
S.T.C.
20X1+10X2 + S1 = 300
4X1 +10X2 + S2= 100
2X1+3X2 +S3 = 38

27. Initial simplex table-1
Cj 400 320 0 0 0 Ratio
CB XB Bi X1 X2 S1 S2 S3 Bi/X1
0 S1 300 20 10 1 0 0 15
0 S2 100 4 10 0 1 0 25
0 S3 38 2 3 0 0 1 19
Zj 0 0 0 0 0 0
Zj-Cj -400 -320 0 0 0
Maximum Negative value zj-cj = -400
Entering variable = X1
Minimum positive ratio = S1
Leaving variable = S1
Key element = 20
Calculation of values of table 2
New main row = R1/20
Remaining row i.e. New R2 = R2-4 X
corresponding element of new main row
New R3 = R3-2X
corresponding element of new main row

28. Table-2
Cj 400 320 0 0 0 Ratio
CB XB Bi X1 X2 S1 S2 S3 Bi/X1
400 X1 15 1 ½ 1/20 0 0 30
0 S2 40 0 8 -1/5 1 0 5
0 S3 8 0 2 -1/10 0 1 4
Zj 6000 400 200 20 0 0
Zj-Cj 0 -120 20 0 0
Maximum Negative value zj-cj = -120
Entering variable = X2
Minimum positive ratio = 4
Leaving variable = S3
Key element = 2
Calculation of values of table 2
New main row = R3/2
Remaining row i.e. New R1 = R1-1/2 x
corresponding element of new main row
New R2 = R2-8X
corresponding element of new main row

29. Table-3
Cj 400 320 0 0 0 Ratio
CB XB Bi X1 X2 S1 S2 S3 Bi/X1
400 X1 13 1 0 3/80 0 -1/4
0 S2 8 0 0 1/10 1 -4
320 X2 4 0 1 -1/2 0 ½
Zj 6480 400 320 7/10 0 6
Zj-Cj 0 0 7/10 0 6
Since all values of Zj-Cj are zero or greater than zero which means optimal solution
has been obtained. 13 units of product X1 and 4 units of product X2 should
produce to maximize the total profit contribution. This combination contributes
profit of Rs. 6480

30. Minimization Problem
Ex :
Minimize (Z) = 3X1 + X2
S.T.C
4X1 + X2 = 4
5X1 + 3X2≥7
3X1+2X2≤6

31. Solution
• Introducing slack and dummy variable :
Minimize (Z) = 3X1 + X2+0S1+0S2+30D1+30D2
S.T.C
4X1 + X2+D1 = 4
5X1 + 3X2-S1+D2=7
3X1+2X2+s2=6

32. Ex:
Minimize Z = 3X1 + 2X2
S.T.C.
2X1+4X2≥10
4X1+2X2 ≥10
X2 ≥4
X1,X2 ≥0

33. Solution
Inequalities of the subjective equations can be changed into
equalities in forms adding surplus variables to the constraint
signs of greater than and equal to (≥)
Minimize (Z) = 3X1+2X2+0S1+0S2+0S3+30D1+30D2+30D3
S.T.C
2X1+4X2-S1+D1 =10
4x1+2X2-S2+D2 =10
X2-S3+D3 =4

34. Initial Simplex table-1
Cj 3 2 0 0 0 30 30 30 Ratio
CB XB Bi X1 X2 S1 S2 S3 D1 D2 D3 Bi/x2
30 D1 10 2 4 -1 0 0 1 0 0 10/4=2.5
30 D2 10 4 2 0 -1 0 0 1 0 10/2=5
30 D3 4 0 1 0 0 -1 0 0 1 4/1=4
Zj 720 180 210 -30 -30 -30 30 30 30
Zj-Cj 177 208 -30 -30 -30 0 0 0
For minimization problem all Zj-Cj should be less than or equal to 0 in the absence
of this further solution is possible.
Most positive Zj-Cj is 208 in X2 column that means entering variable is X2 and least
positive ratio is 2.5 in R1 that means D1 is leaving variable Key element = 4
For next table New R1= R1/4, R2 = R2-2xcorresponding value of R1
For R3 = R3-1 X corresponding value of R3

35. Table-2
Cj 3 2 0 0 0 30 30 30 Ratio
CB XB Bi X1 X2 S1 S2 S3 D1 D2 D3 Bi/x1
2 X2 3/2 1/2 1 -1/4 0 0 ¼ 0 0 5
30 D2 5 3 0 ½ -1 0 -1/2 1 0 5/3=1.67
30 D3 3/2 -1/2 0 1/4 0 -1 -1/4 0 1 -
Zj 198 80 2 22 -30 -30 -22 30 30
Zj-Cj 77 0 22 -30 -30 -52 0 0
For minimization problem all Zj-Zj should be less than or equal to 0 in the absence
of this further solution is possible.
Most positive Zj-Cj is 77 in X1 column that means entering variable is X1 and least
positive ratio is 1.67 in R2 that means D2 is leaving variable Key element = 3
For next table New R2= R2/3, R1 = R2-1/2xcorresponding value of R1
For R3 = R3-(-1/2) X corresponding value of R3

36. Table-3
Cj 3 2 0 0 0 30 30 30 Ratio
CB XB Bi X1 X2 S1 S2 S3 D1 D2 D3 Bi/S1
2 X2 5/3 0 1 -1/3 1/6 0 1/3 -1/6 0 -
3 X1 5/3 1 0 1/6 -1/3 0 -1/6 1/3 0 10
30 D3 7/3 0 0 1/3 -1/6 -1 -1/3 1/6 1 7
Zj 78.33 3 2 9.83 -
5.67
-30 -9.83 5.67 30
Zj-Cj 0 0 9.83 5.67 -30 -20.1 -24.3 0
For minimization problem all Zj-Zj should be less than or equal to 0 in the absence
of this further solution is possible.
Most positive Zj-Cj is 9.83 in S1 column that means entering variable is S1 and least
positive ratio is 7 in R3 that means D3 is leaving variable Key element =1/ 3
For next table New R3= R3/1/3, R1 = R1-(-1/3)x corresponding value of R1
For R2 = R2-(-1/6) X corresponding value of R2

37. Table-4
Cj 3 2 0 0 0 30 30 30 Ratio
CB XB Bi X1 X2 S1 S2 S3 D1 D2 D3 Bi/x1
2 X2 4 0 1 0 0 -1 0 0 1
3 X1 ½ 1 0 0 -1/4 ½ 0 ¼ -1/2
0 S1 7 0 0 1 -1/2 -3 -1 ½ 3
Zj 9.5 3 2 0 -3/4 -1/4 0 ¾ ¼
Zj-Cj 0 0 0 -3/4 -1/4 -30 -117/4 -117/4
Since all Zj-Cj are negative or Zero so further solution is not possible
So, minimum Z =9.5, X2=4, X1 =1/2

38. H.W
• Minimize Z = 200X1 + 800 X2
• S.T.C
25X1+50X2 = 750
X1≤100
X2≥70
And
X1,x2 ≥0