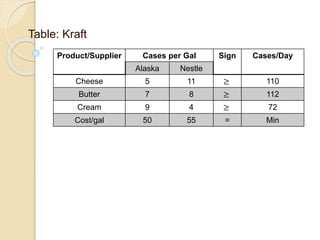
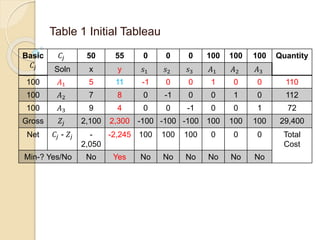
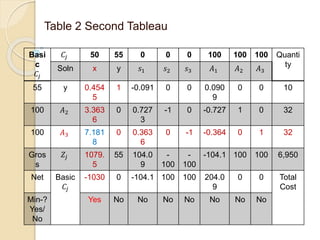
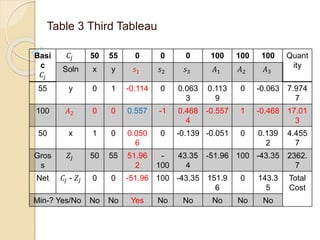
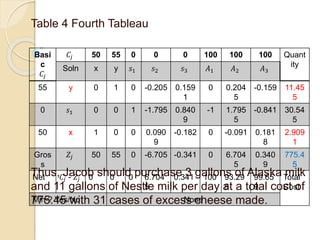
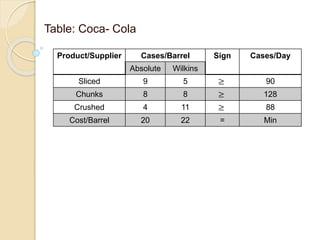
The document describes solving a minimization model using the simplex method. Jacob at Kraft Foods wants to determine the supply mix that will result in minimum cost to produce at least 110 cases of cheese, 112 cases of butter, and 72 cases of cream per day. The simplex method is used over 4 steps to determine that purchasing 10 gallons of Alaska milk and 7.9747 gallons of Nestle milk per day will result in a total minimum cost of $2362.7.

1. Solving Minimization Model by Simplex Method

2. Example 1: Kraft
Jacob is the Purchasing Manager of Kraft
Foods and he wants to determine the supply mix
that will result on minimum cost. He is able to
determine the data necessary for him to make a
decision. A gallon of Alaska milk can produce 5
cases of cheese, 7 cases of butter, and 9 cases of
cream. A gallon of Nestle milk can produce 11
cases of cheese, 8 cases of butter, and 4 cases of
cream. He must produce at least 110 cases of
cheese, 112 cases of butter, and 72 cases of
cream per day. Alaska milk costs 50 dollars per
gallon while Nestle costs 55 dollars per gallon.
How many gallons of Alaska milk and Nestle
milk should be purchase per day to minimize
costs? How much is the total cost?

3. Table: Kraft
Product/Supplier Cases per Gal Sign Cases/Day
Alaska Nestle
Cheese 5 11 ≥ 110
Butter 7 8 ≥ 112
Cream 9 4 ≥ 72
Cost/gal 50 55 = Min

4. Minimize E = 50x + 55y
Subject to:
5x + 11y ≥ 110
7x + 8y ≥ 112
9x + 4y ≥ 72
x, y ≥ 0

5. Step 1: Develop the initial tableau.
1. Set up the variables:
x = number of gallons of Alaska milk to be purchased
per day
y = number of gallons of Nestle milk to be purchased
per day
𝑠1= slack 1 or excess cases of constraint A(cheese)
𝑠2= slack 2 or excess cases of constraint B(butter)
𝑠3= slack 3 or excess cases of constraint C(cream)
𝐴1= artificial variable 1 or initial positive solution for
constraint A
𝐴2= artificial variable 2 or initial positive solution for
constraint B
𝐴3= artificial variable 3 or initial positive solution for
constraint C

6. 2. Set up the objective function where a relatively
high cost is assigned per unit of an artificial variable
(100 dollars for this case):
Minimize:
E = 50x + 55y +0𝑠1+0𝑠2+0𝑠3+100𝐴1+100𝐴2+100𝐴3
Copy the coefficients to the Cj row. Assign the
artificial variables as the initial solution and copy
the coefficient to the Cj column.

7. 3. Convert the constraints into equalities.
Constraint A(cheese)
5x + 11y ≥ 110
5x + 11y −1𝑠1+0𝑠2+0𝑠3+1𝐴1+0𝐴2+0𝐴3 = 110
Constraint B(butter)
7x + 8y ≥ 112
7x + 8y +0𝑠1 − 1𝑠2+0𝑠3+0𝐴1+1𝐴2+0𝐴3 = 112
Constraint C(cream)
9x + 4y ≥ 72
9x + 4y +0𝑠1+0𝑠2 − 1𝑠3+0𝐴1+0𝐴2+1𝐴3 = 72
Copy the coefficients to the 𝐴1, 𝐴2, and 𝐴3 rows.

8. 4. Compute the 𝑍𝑗 values.
𝑍𝑗 = sumproduct(basic 𝐶𝑗 column, variable
column)
2,100 = 100(5)+100(7)+100(9)
2,300 = 100(11)+100(8)+100(4)
- 100 = 100(-1)+100(0)+100(0)
- 100 = 100(0)+100(-1)+100(0)
- 100 = 100(0)+100(0)+100(-1)
100 = 100(1)+100(0)+100(0)
100 = 100(0)+100(1)+100(0)
100 = 100(0)+100(0)+100(1)
29,400 = 100(110)+100(112)+100(72)
= 29,400 dollars of total cost for this
solution

9. 5. Compute the (𝐶𝑗 - 𝑍𝑗) values.
(𝐶𝑗 - 𝑍𝑗) = (𝐶𝑗 row) – (𝑍𝑗 row)
- 2050 = 50 - 2100
- 2245 = 55 - 2300
100 = 0 – (-100)
100 = 0 – (-100)
100 = 0 – (-100)
0 = 100 – 100
0 = 100 – 100
0 = 100 – 100

10. 6. Determine the minimum negative (𝐶𝑗 - 𝑍𝑗) value.
-2245 = - minimum(-2050, -2245, 100, 100, 100, 0,
0, 0)
= pivot column is y.

11. Table 1 Initial Tableau
Basic
𝐶𝑗
𝐶𝑗 50 55 0 0 0 100 100 100 Quantity
Soln x y 𝑠1 𝑠2 𝑠3 𝐴1 𝐴2 𝐴3
100 𝐴1 5 11 -1 0 0 1 0 0 110
100 𝐴2 7 8 0 -1 0 0 1 0 112
100 𝐴3 9 4 0 0 -1 0 0 1 72
Gross 𝑍𝑗 2,100 2,300 -100 -100 -100 100 100 100 29,400
Net 𝐶𝑗 - 𝑍𝑗 -
2,050
-2,245 100 100 100 0 0 0 Total
Cost
Min-? Yes/No No Yes No No No No No No

12. Step 2: Determine the pivot row
1. Compute the quantity ratio (𝑄 𝑟):
𝑄 𝑟 = Q/pivot column
10 = 110/11
14 = 112/8
18 = 72/4
2. Compute the minimum positive quantity ratio
(𝑄 𝑟):
10 = +minimum (10, 14, 18)
= pivot row is 𝐴1

13. 3. Determine the pivot number (𝑃𝑛):
11 = intersection of pivot column and pivot row
Step 3: Develop the second tableau.
1. Replace the pivot row with the pivot column in
the
solution mix:
Exit = 100 𝐴1
Enter = 55y

14. 2. Replace the 𝐴1 row of the initial tableau with the y
row in the second tableau:
y row = 𝐴1 row of initial tableau/pivot number
0.4545 = 5/11
1 = 11/11
-0.091 = -1/11
0 = 0/11
0 = 0/11
0.0909 = 1/11
0 = 0/11
0 = 0/11
10 = 110/11

15. 3. Replace the 𝐴2row of the initial tableau with new values in
the second tableau:
New 𝐴2 row = old 𝐴2 row – (number in old 𝐴2 row
and pivot column)(y row)
3.3636 = 7 - 8(0.4545)
0 = 8 – 8(1)
0.7273 = 0 – 8(-0.091)
-1 = -1 – 8(0)
0 = 0 – 8(0)
-0.727 = 0 – 8(0.0909)
1 = 1 – 8(0)
0 = 0 – 8(0)
32 = 112 – 8(10)

16. 4. Replace the 𝐴3row of the initial tableau with new
values in the second tableau:
New 𝐴3 row = old 𝐴3 row – (number in old 𝐴3 row
and pivot column)(y row)
7.1818 = 9 – 4(0.4545)
0 = 4 – 4(1)
0.3636 = 0 – 4(-0.091)
0 = 0 – 4(0)
-1 = -1 – 4(0)
-0.364 = 0 – 4(0.909)
0 = 0 – 4(0)
1 = 1 – 4(0)
32 = 72 – 4(10)

17. 5. Compute the 𝑍𝑗 values.
𝑍𝑗 = sumproduct(basic 𝐶𝑗 column, variable
column)
1079.5 = 55(0.4545)+100(3.3636)+100(7.1818)
55 = 55(1)+100(0)+100(0)
104.09 = 55(-0.091)+100(0.7273)+100(0.3636)
- 100 = 55(0)+100(-1)+100(0)
- 100 = 55(0)+100(0)+100(-1)
-104.1 = 55(0.0909)+100(-0.727)+100(-0.364)
100 = 55(0)+100(1)+100(0)
100 = 55(0)+100(0)+100(1)
6,950 = 55(10)+100(32)+100(32)
= 6,960 dollars of total cost for this solution

18. 6. Compute the (𝐶𝑗 - 𝑍𝑗) values.
(𝐶𝑗 - 𝑍𝑗) = (𝐶𝑗 row) – (𝑍𝑗 row)
- 1030 = 50 – 1079.5
0 = 55 - 55
-104.1 = 0 – 104.09
100 = 0 – (-100)
100 = 0 – (-100)
204.09 = 100 – (-104.1)
0 = 100 – 100
0 = 100 – 100

19. 7. Determine the minimum negative (𝐶𝑗 - 𝑍𝑗) value.
-1030 =-minimum(-1030, 0, -104.1, 100, 100,
204.09,0, 0)
= pivot column is x.

20. Table 2 Second Tableau
Basi
c
𝐶𝑗
𝐶𝑗 50 55 0 0 0 100 100 100 Quanti
tySoln x y 𝑠1 𝑠2 𝑠3 𝐴1 𝐴2 𝐴3
55 y 0.454
5
1 -0.091 0 0 0.090
9
0 0 10
100 𝐴2 3.363
6
0 0.727
3
-1 0 -0.727 1 0 32
100 𝐴3 7.181
8
0 0.363
6
0 -1 -0.364 0 1 32
Gros
s
𝑍𝑗 1079.
5
55 104.0
9
-
100
-
100
-104.1 100 100 6,950
Net Basic
𝐶𝑗
-1030 0 -104.1 100 100 204.0
9
0 0 Total
Cost
Min-?
Yes/
No
Yes No No No No No No No

21. Step 4: Determine the pivot row
1. Compute the quantity ratio (𝑄 𝑟):
𝑄 𝑟 = Q/pivot column
22 = 10/0.4545
9.5135 = 32/3.3636
4.4557 = 32/7.1818
2. Compute the minimum positive quantity ratio
(𝑄 𝑟):
4.4557 = +minimum (22, 9.5135, 4.4557)
= pivot row is 𝐴3

22. 3. Determine the pivot number (𝑃𝑛):
7.1818 = intersection of pivot column and pivot
row
Step 3: Develop the third tableau.
1. Replace the pivot row with the pivot column in
the
solution mix:
Exit = 100 𝐴3
Enter = 50x

23. 2. Replace the 𝐴3 row of the second tableau with the x
row in the third tableau:
x row = 𝐴3 row of second tableau/pivot number
1 = 7.1818/7.1818
0 = 0/7.1818
0.0506 = 0.3636/7.1818
0 = 0/7.1818
-0.139 = -1/7.1818
-0.051 = -0.364/7.1818
0 = 0/7.1818
01392 = 1/7.1818
4.4557 = 32/7.1818

24. 3. Replace the y row of the second tableau with new
values in the third tableau:
New y row = old y row – (number in old y row
and pivot column)(x row)
0 = 0.4545 – 0.4545(1)
1 = 1 – 0.4545(0)
-0.114 = -0.091 – 0.4545(0.0506)
0 = 0 – 0.4545(0)
0.0633 = 0 – 0.4545(-0.139)
0.1139 = 0.0909 – 0.4545(-0.051)
0 = 0 – 0.4545(0)
-0.063 = 0 – 0.4545(0.1392)
7.9747 = 10 – 0.4545(4.4557)

25. 4. Replace the 𝐴2row of the second tableau with new
values in the third tableau:
New 𝐴2 row = old 𝐴2 row – (number in old 𝐴2 row
and pivot column)(x row)
0 = 3.3636 – 3.3636(1)
0 = 0 – 3.3636(0)
0.557 = 0.7273 – 3.3636(0.0506)
-1 = -1 – 3.3636(0)
0.4684 = 0 – 3.3636(-0.139)
-0.557 = -0.727 – 3.3636(-0.051)
1 = 1 – 3.3636(0)
-0.468 = 0 – 3.3636(0.1392)
17.013 = 32 – 3.3636(4.4557)

26. 5. Compute the 𝑍𝑗 values.
𝑍𝑗 = sumproduct(basic 𝐶𝑗 column, variable column)
50 = 55(0)+100(0)+50(1)
55 = 55(1)+100(0)+50(0)
51.962 = 55(-0.114)+100(0.557)+50(0.0506)
- 100 = 55(0)+100(-1)+50(0)
43.354 = 55(0.0633)+100(0.4684)+50(-0.139)
-51.96 = 55(0.1139)+100(-0.557)+50(-0.051)
100 = 55(0)+100(1)+50(0)
-43.35 = 55(-0.063)+100(-0.468)+50(0.1392)
2362.7 = 55(7.9747)+100(17.013)+50(4.4557)
= 2362.7 dollars of total cost for this solution

27. 6. Compute the (𝐶𝑗 - 𝑍𝑗) values.
(𝐶𝑗 - 𝑍𝑗) = (𝐶𝑗 row) – (𝑍𝑗 row)
0 = 50 – 50
0 = 55 - 55
-51.96 = 0 – 51.962
100 = 0 – (-100)
-43.35 = 0 – 43.354
151.96 = 100 – (-51.96)
0 = 100 – 100
143.35 = 100 – (-43.35)

28. 7. Determine the minimum negative (𝐶𝑗 - 𝑍𝑗)
value.
-51.96 =-minimum(0, 0, -51.96, 100, -43.35,
151.96,0,
143.35)
= pivot column is 𝑠1.

29. Table 3 Third Tableau
Basi
c
𝐶𝑗
𝐶𝑗 50 55 0 0 0 100 100 100 Quant
itySoln x y 𝑠1 𝑠2 𝑠3 𝐴1 𝐴2 𝐴3
55 y 0 1 -0.114 0 0.063
3
0.113
9
0 -0.063 7.974
7
100 𝐴2 0 0 0.557 -1 0.468
4
-0.557 1 -0.468 17.01
3
50 x 1 0 0.050
6
0 -0.139 -0.051 0 0.139
2
4.455
7
Gros
s
𝑍𝑗 50 55 51.96
2
-
100
43.35
4
-51.96 100 -43.35 2362.
7
Net 𝐶𝑗 - 𝑍𝑗 0 0 -51.96 100 -43.35 151.9
6
0 143.3
5
Total
Cost
Min-? Yes/No No No Yes No No No No No

30. Step 6: Determine the pivot row
1. Compute the quantity ratio (𝑄 𝑟):
𝑄 𝑟 = Q/pivot column
-70 = 7.9747/-0.114
30.545 = 17.013/0.557
88 = 4.4557/0.0506
2. Compute the minimum positive quantity ratio
(𝑄 𝑟):
30.545 = +minimum (-70, 30.545, 88)
= pivot row is 𝐴2

31. 3. Determine the pivot number (𝑃𝑛):
0.557 = intersection of pivot column and pivot
row
Step 3: Develop the fourth tableau.
1. Replace the pivot row with the pivot column in
the
solution mix:
Exit = 100 𝐴2
Enter = 0𝑠1

32. 2. Replace the 𝐴2 row of the third tableau with the 𝑠1
row in the fourth tableau:
𝑠1 row = 𝐴2 row of third tableau/pivot number
0 = 0/0.557
0 = 0/0.557
1 = 0.557/0.557
-1.795 = -1/0.557
0.8409 = 0.4684/0.557
-1 = - 0.557/0.557
1.7955 = 1/0.557
-0.841 = -0.468/0.557
30.545 = 17.013/0.557

33. 3. Replace the y row of the third tableau with new
values in the fourth tableau:
New y row = old y row – (number in old y row
and pivot column)(x row)
0 = 0 – (- 0.114)(0)
1 = 1 – (- 0.114)(0)
0 = - 0.114 – (- 0.114)(1)
-0.205 = 0 – (- 0.114)(-1.795)
0.1591 = 0.0633 – (- 0.114)(0.8409)
0 = 0.1139 – (- 0.114)(-1)
0.2045 = 0 – (- 0.114)(1.7955)
-0.159 = - 0.063 – (- 0.114)(-0.841)
11.455 = 7.9747 – (- 0.114)(30.545)

34. 4. Replace the x row of the third tableau with new
values in the fourth tableau:
New x row = old x row – (number in old x row
and pivot column)(𝑠1 row)
1 = 1 – 0.0506(0)
0 = 0 – 0.0506(0)
0 = 0.0506 – 0.0506(1)
0.0909 = 0 – 0.0506(-1.795)
-0.182 = -0.139 – 0.0506(0.8409)
0 = - 0.051 – 0.0506(-1)
-0.091 = 0 – 0.0506(1.7955)
0.1818 = 0.1392 – 0.0506(-0.841)
2.9091 = 4.4557 – 0.0506(30.545)

35. 5. Compute the 𝑍𝑗 values.
𝑍𝑗 = sumproduct(basic 𝐶𝑗 column, variable column)
50 = 55(0)+0(0)+50(1)
55 = 55(1)+0(0)+50(0)
0 = 55(0)+0(1)+50(0)
- 6.705 = 55(-0.205)+0(-1.795)+50(0.0909)
-0.341 = 55(0.1591)+0(0.8409)+50(-0.182)
0 = 55(0)+0(-1)+50(0)
6.7045 = 55(0.2045)+0(1.7955)+50(-0.091)
0.3409 = 55(-0.159)+0(-0.841)+50(0.1818)
775.45 = 55(11.455)+0(30.545)+50(2.9091)
= 775.45 dollars of total cost for this solution

36. 6. Compute the (𝐶𝑗 - 𝑍𝑗) values.
(𝐶𝑗 - 𝑍𝑗) = (𝐶𝑗 row) – (𝑍𝑗 row)
0 = 50 – 50
0 = 55 - 55
0 = 0 – 0
6.7045 = 0 – (-6.705)
0.341 = 0 – (-0.341)
100 = 100 – 0
93.295 = 100 – 6.7045
99.659 = 100 – 0.3409

37. 7. Determine the minimum negative (𝐶𝑗 - 𝑍𝑗) value.
NONE = - minimum(0, 0, 6.7045, 0.341, 100,
93.295,
99.659)
= FINAL tableau is reached.

38. 8. Determine the final solution:
y = 11.455 (11 gallons of Nestle milk should be
purchased per day)
𝑠1 = 30.545 (31 cases of excess cheese are
produced
per day)
x = 2.9091 (3 gallons of Alaska milk should be
purchased per day)
𝑍𝑗 = 775.45 (775.45 is the total cost per day)

39. Table 4 Fourth Tableau
Thus, Jacob should purchase 3 gallons of Alaska milk
and 11 gallons of Nestle milk per day at a total cost of
775.45 with 31 cases of excess cheese made.
Basi
c
𝐶𝑗
𝐶𝑗 50 55 0 0 0 100 100 100 Quant
itySoln x y 𝑠1 𝑠2 𝑠3 𝐴1 𝐴2 𝐴3
55 y 0 1 0 -0.205 0.159
1
0 0.204
5
-0.159 11.45
5
0 𝑠1 0 0 1 -1.795 0.840
9
-1 1.795
5
-0.841 30.54
5
50 x 1 0 0 0.090
9
-0.182 0 -0.091 0.181
8
2.909
1
Gros
s
𝑍𝑗 50 55 0 -6.705 -0.341 0 6.704
5
0.340
9
775.4
5
Net 𝐶𝑗 - 𝑍𝑗 0 0 0 6.704
5
0.341 100 93.29
5
99.65
9
Total
Cost
Min-? Yes/No None

40. Example 2: Coca-Cola
Karen is the Head Buyer of Coca-Cola and she
wants to determine the supply mix that will result on
minimum cost. She is able to determine the data
necessary for her to make a decision. A kilogram of
Equal sweetener can produce 4 liters of Coke Lite, 6
liters of Sprite Lite, and 10 liters of Coke Zero. A
kilogram of Nutra sweetener can produce 12 liters of
Coke Lite, 8 liters of Sprite Lite, and 5 liters of Coke
Zero. Karen must produce at least 96 liters of Coke
Lite, 96 liters of Sprite Lite, and 100 liters of Coke Zero
per day. Equal sweetener costs 27 dollars per kilogram
while Nutra sweetener costs 30 dollars per kilogram.
How many kilograms of Equal sweetener and
Nutra sweetener should she purchase per day to
minimize costs? How much is the total cost?

41. Example 3:
Lester is the Production Analyst of Dole Pineapple and
he wants to determine the supply mix that will result to
minimum cost. He is able to determine the data
necessary for him to make a decision. A barrel of
Absolute water can produce 9 cases of sliced
pineapple, 8 cases of pineapple chunks, and 4 cases
of crushed pineapple. A barrel of Wilkins water can
produce 5 cases of sliced pineapple, 8 cases of
pineapple chunks, and 11 cases of crushed pineapple.
Lester must produce at least 90 cases of sliced
pineapple, 128 cases of pineapple chunks, and 88
cases of crushed pineapple per day. Absolute water
costs 20 per barrel while Wilkins water costs 22 per
barrel.
How many barrels of Absolute water and Wilkins water
should he purchase per day to minimize costs? How
much is the total cost?

42. Table: Coca- Cola
Product/Supplier Cases/Barrel Sign Cases/Day
Absolute Wilkins
Sliced 9 5 ≥ 90
Chunks 8 8 ≥ 128
Crushed 4 11 ≥ 88
Cost/Barrel 20 22 = Min