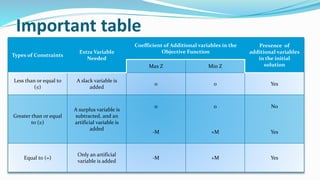
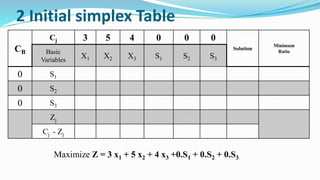
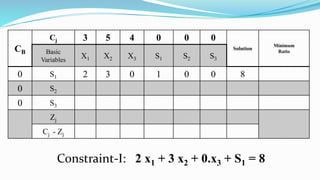
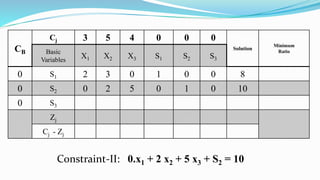
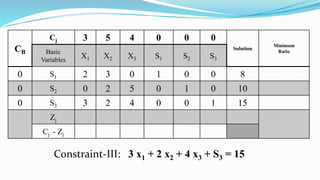
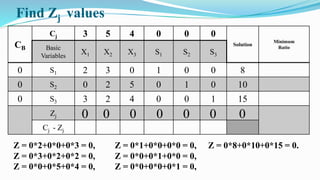
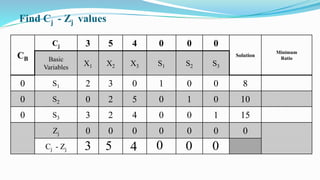
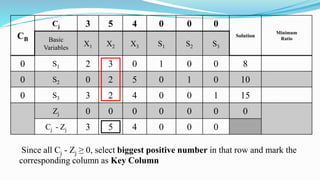
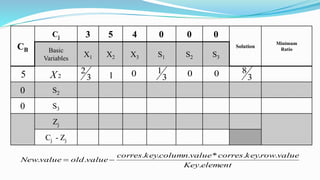
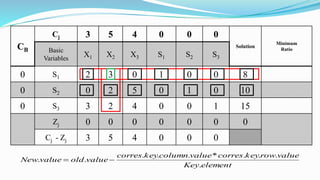
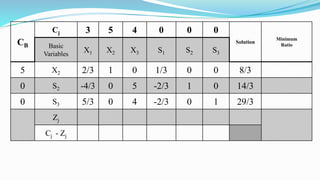
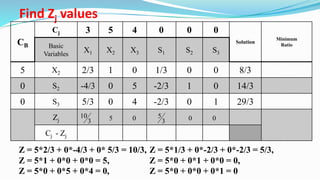
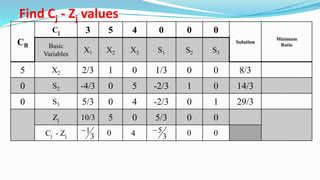
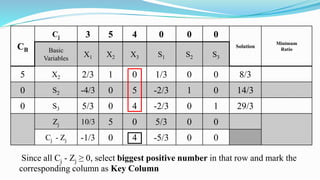
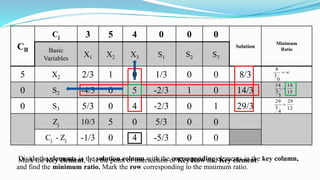
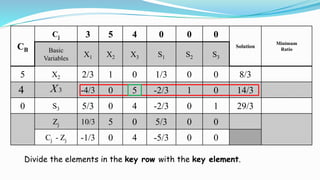
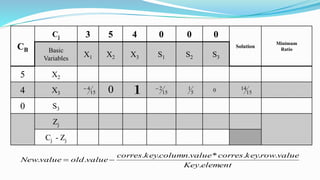
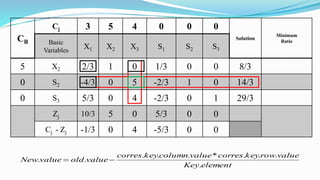
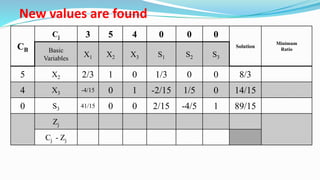
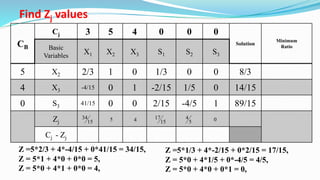
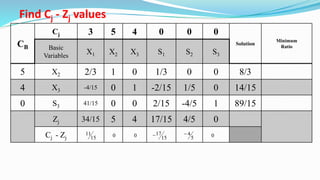
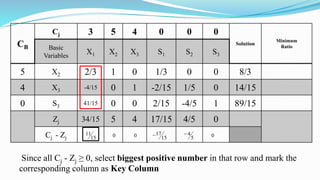
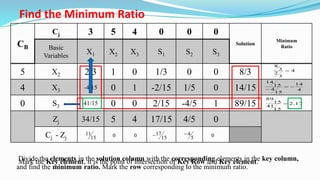
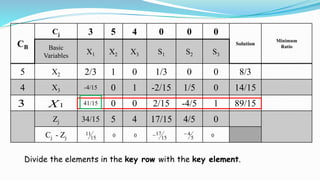
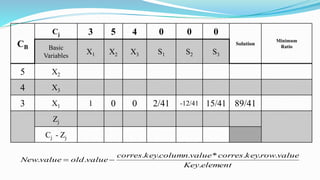
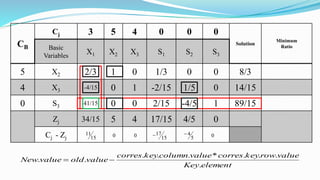
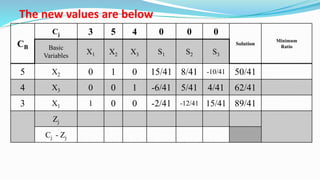
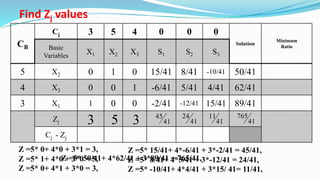
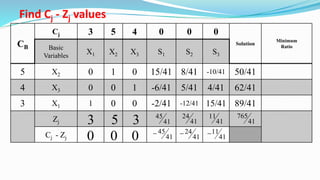
The document outlines the application of the simplex method to solve a linear programming problem aimed at maximizing the objective function Z = 3x1 + 5x2 + 4x3 under certain constraints. It details the formulation of the mathematical model, including the addition of slack variables to convert inequalities into equations, and presents the step-by-step process of the simplex algorithm through various iterations. Through these steps, it demonstrates how to determine optimal solutions and necessary calculations required in the process.

1. Simplex Method
Mr. P.Praveen Babu
Assistant Professor
MREC(A)

2. Example - II
 Solve LP Problem using Simplex method
 Maximize Z = 3 x1 + 5 x2 + 4 x3
 Subject to the constraints:
 (i) 2 x1 + 3 x2 ≤ 8 (ii) 2 x2 + 5 x3 ≤ 10
 (iii) 3 x1 + 2 x2 + 4 x3 ≤ 15
 Where x1 , x2 , x3 ≥ 0

3. Important table
Types of Constraints
Extra Variable
Needed
Coefficient of Additional variables in the
Objective Function
Presence of
additional variables
in the initial
solutionMax Z Min Z
Less than or equal to
(≤)
A slack variable is
added
0 0 Yes
Greater than or equal
to (≥)
A surplus variable is
subtracted, and an
artificial variable is
added
0
-M
0
+M
No
Yes
Equal to (=)
Only an artificial
variable is added
-M +M Yes

4. 1. Formulation of mathematical model
 Type of constraints = less than or equal to (≤)
 Therefore, we should add slack variable to the
constraints and objective function as well.
 But the coefficients of slack variables must be zeros
in the Objective function.

5. 1. Formulation of mathematical model
 Objective function:
 Maximize Z = 3 x1 + 5 x2 + 4 x3 +0.S1 + 0.S2 + 0.S3
 Subject to constraints:
 2 x1 + 3 x2 + 0.x3 + S1 = 8
 0.x1 + 2 x2 + 5 x3 + S2 = 10
 3 x1 + 2 x2 + 4 x3 + S3 = 15
 x1 , x2 , x3 ≥ 0
Adding slack variables
to the constraints
converts the linear
inequalities to the
equations.

6. 2 Initial simplex Table
CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
0 S1
0 S2
0 S3
Zj
Cj - Zj
Maximize Z = 3 x1 + 5 x2 + 4 x3 +0.S1 + 0.S2 + 0.S3

7. Constraint-I: 2 x1 + 3 x2 + 0.x3 + S1 = 8
CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
0 S1 2 3 0 1 0 0 8
0 S2
0 S3
Zj
Cj - Zj

8. Constraint-II: 0.x1 + 2 x2 + 5 x3 + S2 = 10
CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
0 S1 2 3 0 1 0 0 8
0 S2 0 2 5 0 1 0 10
0 S3
Zj
Cj - Zj

9. Constraint-III: 3 x1 + 2 x2 + 4 x3 + S3 = 15
CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
0 S1 2 3 0 1 0 0 8
0 S2 0 2 5 0 1 0 10
0 S3 3 2 4 0 0 1 15
Zj
Cj - Zj

10. Find Zj values
CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
0 S1 2 3 0 1 0 0 8
0 S2 0 2 5 0 1 0 10
0 S3 3 2 4 0 0 1 15
Zj
Cj - Zj
Z = 0*2+0*0+0*3 = 0,
Z = 0*3+0*2+0*2 = 0,
Z = 0*0+0*5+0*4 = 0,
Z = 0*1+0*0+0*0 = 0,
Z = 0*0+0*1+0*0 = 0,
Z = 0*0+0*0+0*1 = 0,
0 0 0 0 0 0
Z = 0*8+0*10+0*15 = 0.
0

11. Find Cj - Zj values
CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
0 S1 2 3 0 1 0 0 8
0 S2 0 2 5 0 1 0 10
0 S3 3 2 4 0 0 1 15
Zj 0 0 0 0 0 0 0
Cj - Zj 3 5 4 0 0 0

12. Test for Optimality : Maximization
 For Maximization Problem:
 If all Cj – Zj ≤ 0 ; then the LP problem is said to be
reached Optimality.

13. CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
0 S1 2 3 0 1 0 0 8
0 S2 0 2 5 0 1 0 10
0 S3 3 2 4 0 0 1 15
Zj 0 0 0 0 0 0 0
Cj - Zj 3 5 4 0 0 0
Since all Cj - Zj ≥ 0, select biggest positive number in that row and mark the
corresponding column as Key Column

14. Find the Minimum Ratio
CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
0 S1 2 3 0 1 0 0 8
0 S2 0 2 5 0 1 0 10
0 S3 3 2 4 0 0 1 15
Zj 0 0 0 0 0 0 0
Cj - Zj 3 5 4 0 0 0
Divide the elements in the solution column with the corresponding elements in the key column,
and find the minimum ratio. Mark the row corresponding to the minimum ratio.
66.2
3
8 
5
2
10 
5.7
2
15 
Mark the Key element, it is the point of intersection of Key Row and Key element.

15. CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
2 3 0 1 0 0 8
0 S2 0 2 5 0 1 0 10
0 S3 3 2 4 0 0 1 15
Zj 0 0 0 0 0 0 0
Cj - Zj 3 5 4 0 0 0
2X5
Divide the elements in the key row with the key element.

16. CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
0 S2
0 S3
Zj
Cj - Zj
2X5 3
2
1 0 3
1 0 0 3
8
elementKey
valuerowkeycorresvaluecolumnkeycorres
valueoldvalueNew
.
...*...
.. 

17. CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
0 S1 2 3 0 1 0 0 8
0 S2 0 2 5 0 1 0 10
0 S3 3 2 4 0 0 1 15
Zj 0 0 0 0 0 0 0
Cj - Zj 3 5 4 0 0 0
elementKey
valuerowkeycorresvaluecolumnkeycorres
valueoldvalueNew
.
...*...
.. 

18. CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 2/3 1 0 1/3 0 0 8/3
0 S2 -4/3 0 5 -2/3 1 0 14/3
0 S3 5/3 0 4 -2/3 0 1 29/3
Zj
Cj - Zj

19. Find Zj values
CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 2/3 1 0 1/3 0 0 8/3
0 S2 -4/3 0 5 -2/3 1 0 14/3
0 S3 5/3 0 4 -2/3 0 1 29/3
Zj
Cj - Zj
Z = 5*2/3 + 0*-4/3 + 0* 5/3 = 10/3,
Z = 5*1 + 0*0 + 0*0 = 5,
Z = 5*0 + 0*5 + 0*4 = 0,
Z = 5*1/3 + 0*-2/3 + 0*-2/3 = 5/3,
Z = 5*0 + 0*1 + 0*0 = 0,
Z = 5*0 + 0*0 + 0*1 = 0
3
10 5 0 3
5 0 0

20. Find Cj - Zj values
CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 2/3 1 0 1/3 0 0 8/3
0 S2 -4/3 0 5 -2/3 1 0 14/3
0 S3 5/3 0 4 -2/3 0 1 29/3
Zj 10/3 5 0 5/3 0 0
Cj - Zj 3
1 0 4 3
5 0 0

21. Test for Optimality : Maximization
 For Maximization Problem:
 If all Cj – Zj ≤ 0 ; then the LP problem is said to be
reached Optimality.

22. CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 2/3 1 0 1/3 0 0 8/3
0 S2 -4/3 0 5 -2/3 1 0 14/3
0 S3 5/3 0 4 -2/3 0 1 29/3
Zj 10/3 5 0 5/3 0 0
Cj - Zj -1/3 0 4 -5/3 0 0
Since all Cj - Zj ≥ 0, select biggest positive number in that row and mark the
corresponding column as Key Column

23. Divide the elements in the solution column with the corresponding elements in the key column,
and find the minimum ratio. Mark the row corresponding to the minimum ratio.
CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 2/3 1 0 1/3 0 0 8/3
0 S2 -4/3 0 5 -2/3 1 0 14/3
0 S3 5/3 0 4 -2/3 0 1 29/3
Zj 10/3 5 0 5/3 0 0
Cj - Zj -1/3 0 4 -5/3 0 0

0
3
8
15
14
5
3
14

12
29
4
3
29

Mark the Key element, it is the point of intersection of Key Row and Key element.

24. Divide the elements in the key row with the key element.
CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 2/3 1 0 1/3 0 0 8/3
-4/3 0 5 -2/3 1 0 14/3
0 S3 5/3 0 4 -2/3 0 1 29/3
Zj 10/3 5 0 5/3 0 0
Cj - Zj -1/3 0 4 -5/3 0 0
3X4

25. CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2
4 X3
0 S3
Zj
Cj - Zj
15
4
0 1 15
2
5
1 0 15
14
elementKey
valuerowkeycorresvaluecolumnkeycorres
valueoldvalueNew
.
...*...
.. 

26. CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 2/3 1 0 1/3 0 0 8/3
0 S2 -4/3 0 5 -2/3 1 0 14/3
0 S3 5/3 0 4 -2/3 0 1 29/3
Zj 10/3 5 0 5/3 0 0
Cj - Zj -1/3 0 4 -5/3 0 0
elementKey
valuerowkeycorresvaluecolumnkeycorres
valueoldvalueNew
.
...*...
.. 

27. CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 2/3 1 0 1/3 0 0 8/3
4 X3 -4/15 0 1 -2/15 1/5 0 14/15
0 S3 41/15 0 0 2/15 -4/5 1 89/15
Zj
Cj - Zj
New values are found

28. Find Zj values
CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 2/3 1 0 1/3 0 0 8/3
4 X3 -4/15 0 1 -2/15 1/5 0 14/15
0 S3 41/15 0 0 2/15 -4/5 1 89/15
Zj
Cj - Zj
Z =5*2/3 + 4*-4/15 + 0*41/15 = 34/15,
Z = 5*1 + 4*0 + 0*0 = 5,
Z = 5*0 + 4*1 + 0*0 = 4,
Z =5*1/3 + 4*-2/15 + 0*2/15 = 17/15,
Z = 5*0 + 4*1/5 + 0*-4/5 = 4/5,
Z = 5*0 + 4*0 + 0*1 = 0,
15
34 5 4 15
17
5
4 0

29. Find Cj - Zj values
CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 2/3 1 0 1/3 0 0 8/3
4 X3 -4/15 0 1 -2/15 1/5 0 14/15
0 S3 41/15 0 0 2/15 -4/5 1 89/15
Zj 34/15 5 4 17/15 4/5 0
Cj - Zj 15
11 0 0 15
17
5
4 0

30. Test for Optimality : Maximization
 For Maximization Problem:
 If all Cj – Zj ≤ 0 ; then the LP problem is said to be
reached Optimality.

31. Since all Cj - Zj ≥ 0, select biggest positive number in that row and mark the
corresponding column as Key Column
CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 2/3 1 0 1/3 0 0 8/3
4 X3 -4/15 0 1 -2/15 1/5 0 14/15
0 S3 41/15 0 0 2/15 -4/5 1 89/15
Zj 34/15 5 4 17/15 4/5 0
Cj - Zj 15
11 0 0 15
17
5
4 0

32. CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 2/3 1 0 1/3 0 0 8/3
4 X3 -4/15 0 1 -2/15 1/5 0 14/15
0 S3 41/15 0 0 2/15 -4/5 1 89/15
Zj 34/15 5 4 17/15 4/5 0
Cj - Zj 15
11 0 0 15
17
5
4 0
Find the Minimum Ratio
Divide the elements in the solution column with the corresponding elements in the key column,
and find the minimum ratio. Mark the row corresponding to the minimum ratio.
4
3
2
3
8

4
14
15
4
15
14


17.2
15
41
15
89

Mark the Key element, it is the point of intersection of Key Row and Key element.

33. CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 2/3 1 0 1/3 0 0 8/3
4 X3 -4/15 0 1 -2/15 1/5 0 14/15
41/15 0 0 2/15 -4/5 1 89/15
Zj 34/15 5 4 17/15 4/5 0
Cj - Zj 15
11 0 0 15
17
5
4 0
1X3
Divide the elements in the key row with the key element.

34. CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2
4 X3
3 X1 1 0 0 2/41 -12/41 15/41 89/41
Zj
Cj - Zj
elementKey
valuerowkeycorresvaluecolumnkeycorres
valueoldvalueNew
.
...*...
.. 

35. CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 2/3 1 0 1/3 0 0 8/3
4 X3 -4/15 0 1 -2/15 1/5 0 14/15
0 S3 41/15 0 0 2/15 -4/5 1 89/15
Zj 34/15 5 4 17/15 4/5 0
Cj - Zj 15
11 0 0 15
17
5
4 0
elementKey
valuerowkeycorresvaluecolumnkeycorres
valueoldvalueNew
.
...*...
.. 

36. CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 0 1 0 15/41 8/41 -10/41 50/41
4 X3 0 0 1 -6/41 5/41 4/41 62/41
3 X1 1 0 0 -2/41 -12/41 15/41 89/41
Zj
Cj - Zj
The new values are below

37. Z =5* 0+ 4*0 + 3*1 = 3,
Z =5* 1+ 4*0 + 3*0 = 5,
Z =5* 0+ 4*1 + 3*0 = 3,
CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 0 1 0 15/41 8/41 -10/41 50/41
4 X3 0 0 1 -6/41 5/41 4/41 62/41
3 X1 1 0 0 -2/41 -12/41 15/41 89/41
Zj
Cj - Zj
Find Zj values
3 5 3
Z =5* 15/41+ 4*-6/41 + 3*-2/41 = 45/41,
Z =5* 8/41+ 4*5/41 + 3*-12/41 = 24/41,
Z =5* -10/41+ 4*4/41 + 3*15/ 41= 11/41,
41
45
41
24
41
11
Z =5* 50/41+ 4*62/41 + 3*89/41 = 765/41,
41
765

38. CB
Cj 3 5 4 0 0 0
Solution
Minimum
RatioBasic
Variables
X1 X2 X3 S1 S2 S3
5 X2 0 1 0 15/41 8/41 -10/41 50/41
4 X3 0 0 1 -6/41 5/41 4/41 62/41
3 X1 1 0 0 -2/41 -12/41 15/41 89/41
Zj
Cj - Zj
Find Cj - Zj values
3 5 3 41
45
41
24
41
11
41
765
0 0 0 41
45
41
24
41
11

39. Result
 LP problem has reached optimality:
 Therefore, X1 = 89/41, X2 = 50/41, X3 = 62/41
 Finally Z = 765/41