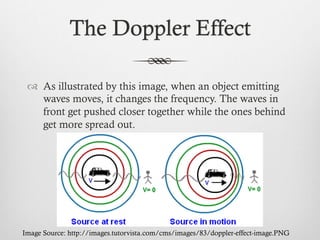
The document explains the Doppler effect, which is the change in frequency of waves due to the relative motion between the source and the observer. It describes how the frequency increases when the source moves towards the observer and decreases when it moves away, using equations and examples to illustrate the concept. Two practical scenarios involving a police car and a goose are presented to demonstrate calculations involving the Doppler effect.

2. The Doppler Effect
™ According to Sheldon Cooper of the Big Bang Theory,
the Doppler effect is “the apparent change in the
frequency of a wave caused by relative motion between
the source of the wave and the observer.”
™ It affects any type of wave including light and sound.
™ The Doppler effect only applies when the motion is
directly towards or away between the source and the
observer.

3. The Doppler Effect
™ As illustrated by this image, when an object emitting
waves moves, it changes the frequency. The waves in
front get pushed closer together while the ones behind
get more spread out.
Image Source: http://images.tutorvista.com/cms/images/83/doppler-effect-image.PNG

4. The Doppler Effect
™ You can see that the wavelength in front of the motion
of the object decreases. Although the object is moving,
the sound speed itself does not change. If the medium
stays the same, the speed also stays constant. Thus, the
frequency increases as a result.
™ It’s the opposite for the waves behind the motion of the
object. The wavelength increases and the frequency
decreases.
™ This relationship can be seen in the following equation:
v=fλ

5. Equations
™ The relationship between the frequencies of the
receiver and the source of the waves is denoted by the
following equation where v is the speed of sound, vr is
the speed of the receiver, vs is the speed of the source
and fr and fs are the frequencies of the source and the
receiver respectively.

6. Equations
™ Numerator:
+ is used when the receiver moves towards the source
- is used when the receiver moves away from the
source
™ Denominator:
- is used when the source moves towards the receiver
+ is used when the source moves away from the
receiver
™ Tip: the sign on top always relates to motion towards,
bottom sign relates to motion away

7. Question
™ You robbed a bank and speed away in a car at 80 m/s.
A police car is chasing you from behind at 95 m/s. Its
siren, sounding at a frequency of 775 Hz, makes you
anxious. Make a prediction. Do you expect the
frequency you hear to be higher or lower? Calculate the
frequency will you hear due to the motion of the cars.
95 m/s
775 Hz 80 m/s
Image Source: http://fc05.deviantart.net/fs71/f/2012/088/2/8/bmw_car_chase_by_domino3d-d4ub8uw.jpg

8. Solution
™ You should expect to hear a higher frequency because
the motion of the police car is headed towards you,
pushing the wave fronts of sound closer together and
increasing the frequency that you’ll hear them at.
™ Looking at the question, you are given vr= 80 m/s,
vs= 95 m/s, and fs= 775 Hz, and you know the speed
of sound in air is 343 m/s. The easy part is plugging
them into the equation. Then you just have to decide
on whether to use + or – signs.

9. Solution
™ Since you are moving away from the police car, you
use a – sign in the numerator, and since the police car
is moving towards you, you use a – sign in the
denominator. Plugging in the numbers gives you:
™ So you get fr= 822 m/s, which is the frequency you
hear from the siren which is higher than 775 m/s as
predicted.

10. Question
™ You are standing beside a lake when suddenly a scary
looking goose comes running through the grass towards you
at a constant speed, honking angrily. You hear a frequency of
84.0 Hz. The goose as it turns out, is not mad at you, but
rather at the kid chasing its goslings, and runs straight
through your legs. After it passes, you hear a frequency of
56.0 Hz. What is the speed of the goose?
Image Source: http://hollypointassociation.org/a_angry_goose_400p.jpg

11. Solution
™ We know 2 frequencies: As the goose comes towards
us and as it goes away from us. So, we need to use 2
equations. We don’t know the actual frequency. With
what we know, these are the 2 equations we get:
™ We have a – in the 1st equation because the goose is
moving towards us, + in the 2nd because it moves away

12. Solution
™ There are two unknowns but that’s okay because the
unknowns are the same in both equations. The actual
frequency stays the same and the speed does too since
the goose is moving at a constant velocity. We divide
the equations by each other so we can cancel out
several parts of them.

13. Solution
™ 84/56 is 3/2. fs and the 343 m/s in the numerator of
the top and the bottom equations cancel out leaving
you with:

14. Clarification
™ If you are confused about the previous slide, this is
where I will explain. If not, skip this slide.
™ These are equivalent to each other because when you
divide by a fraction, you simply multiply by the
reciprocal (flip the fraction). Since 343 m/s cancels
out, you are left with:

15. Solution
™ Cross multiply, distribute, gather the like terms on
separate sides to isolate the variable vs. Then solve for
vs.
™ Final answer: The goose was running at 68.6 m/s