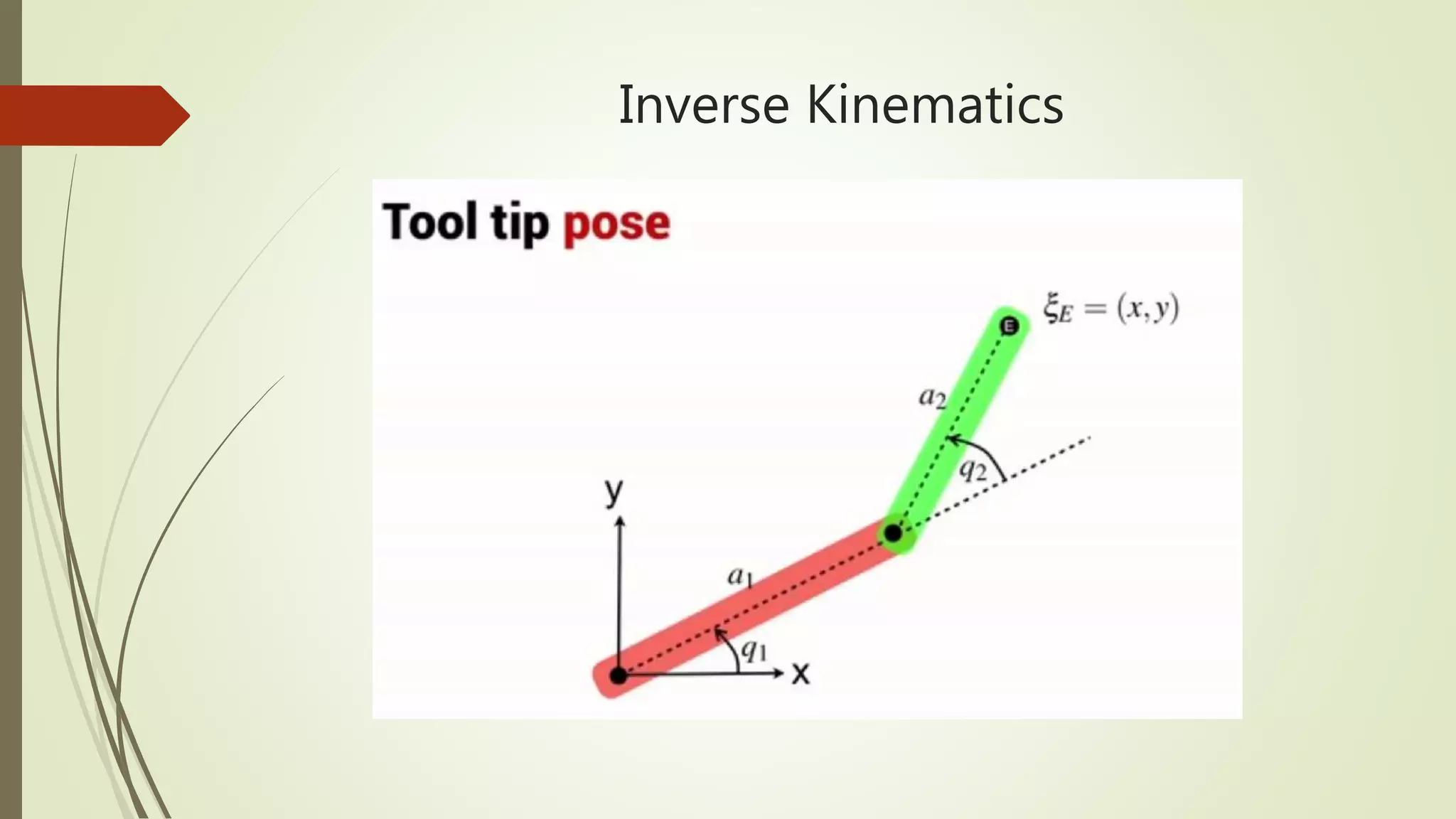
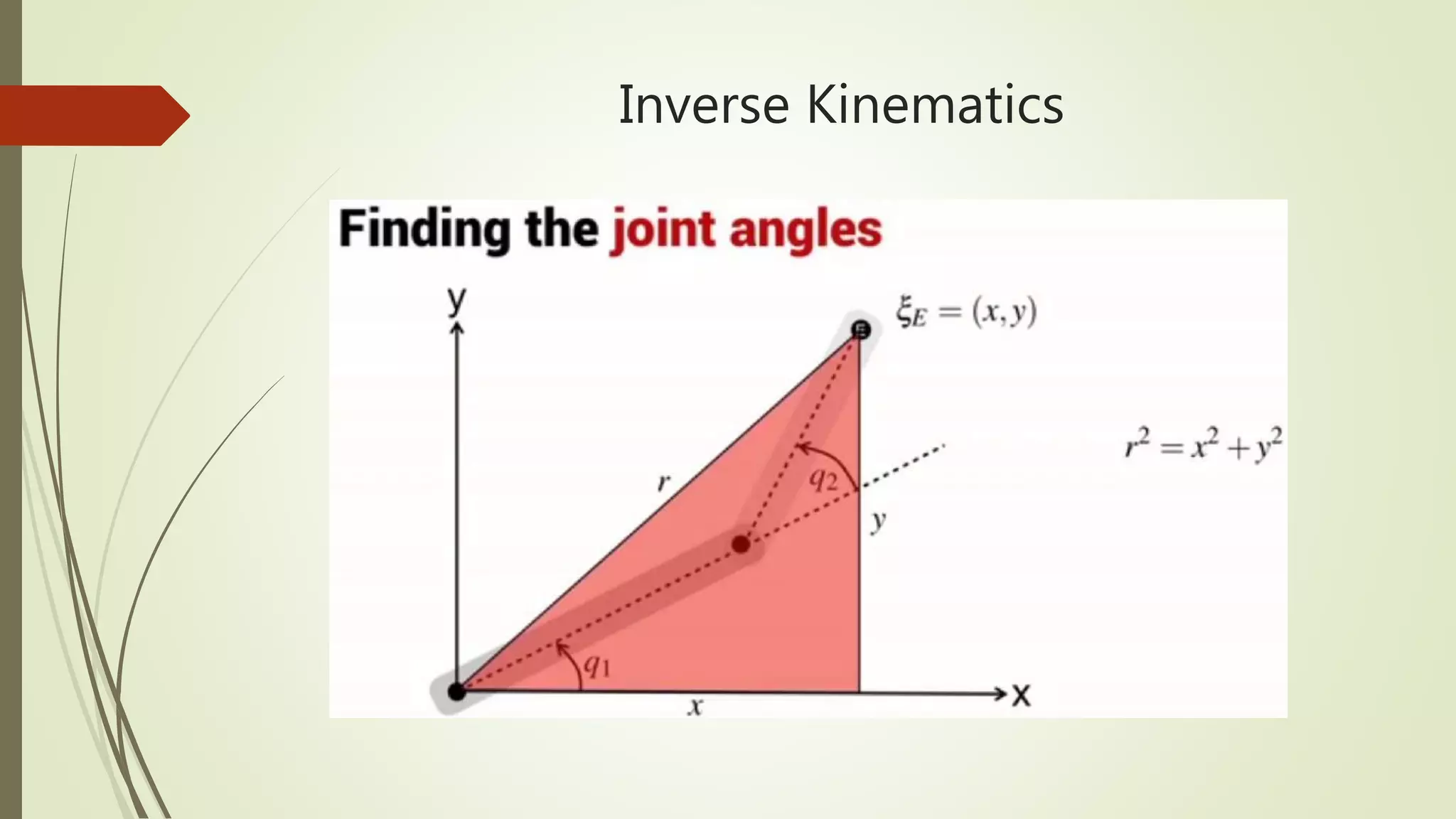
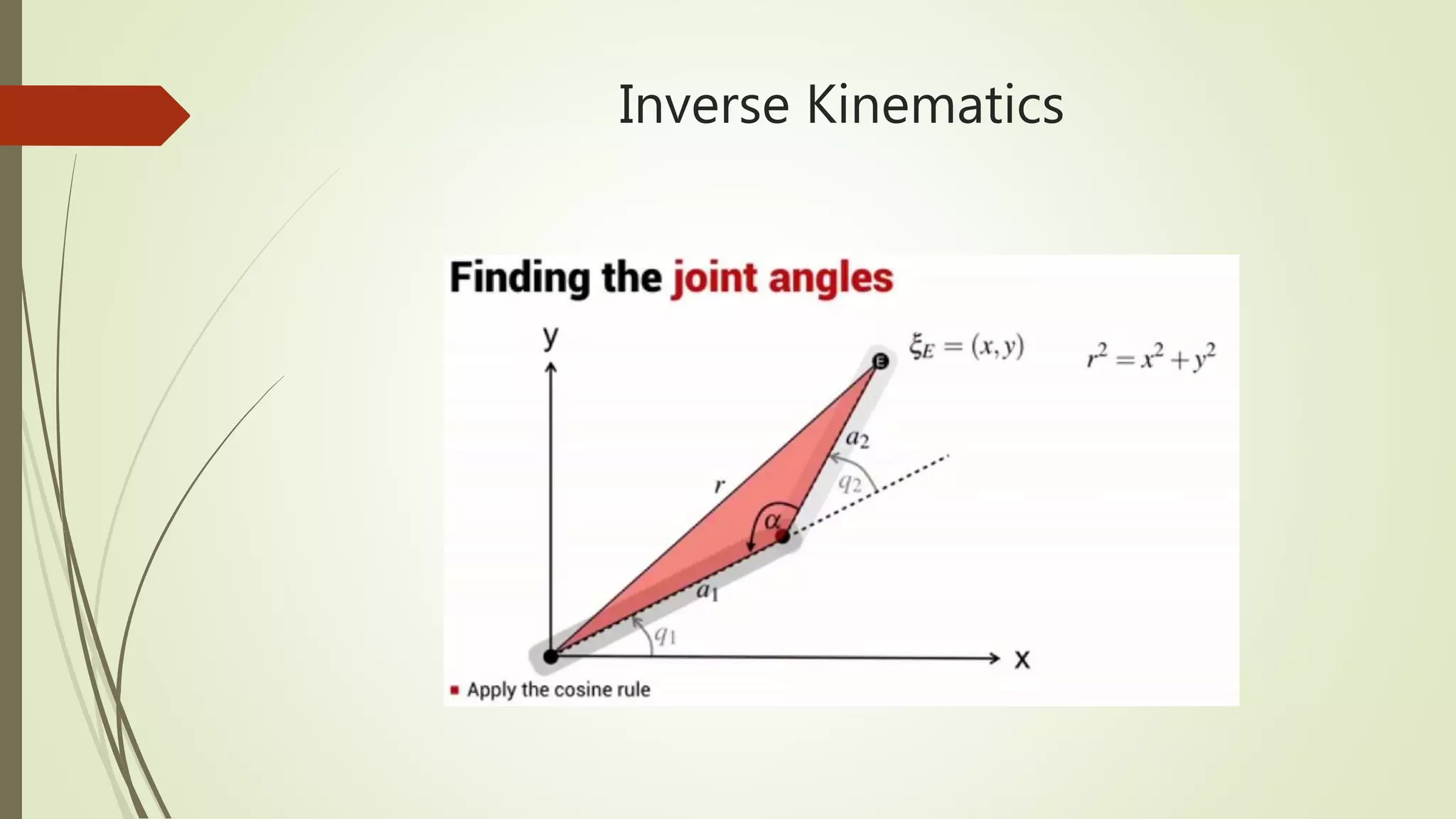
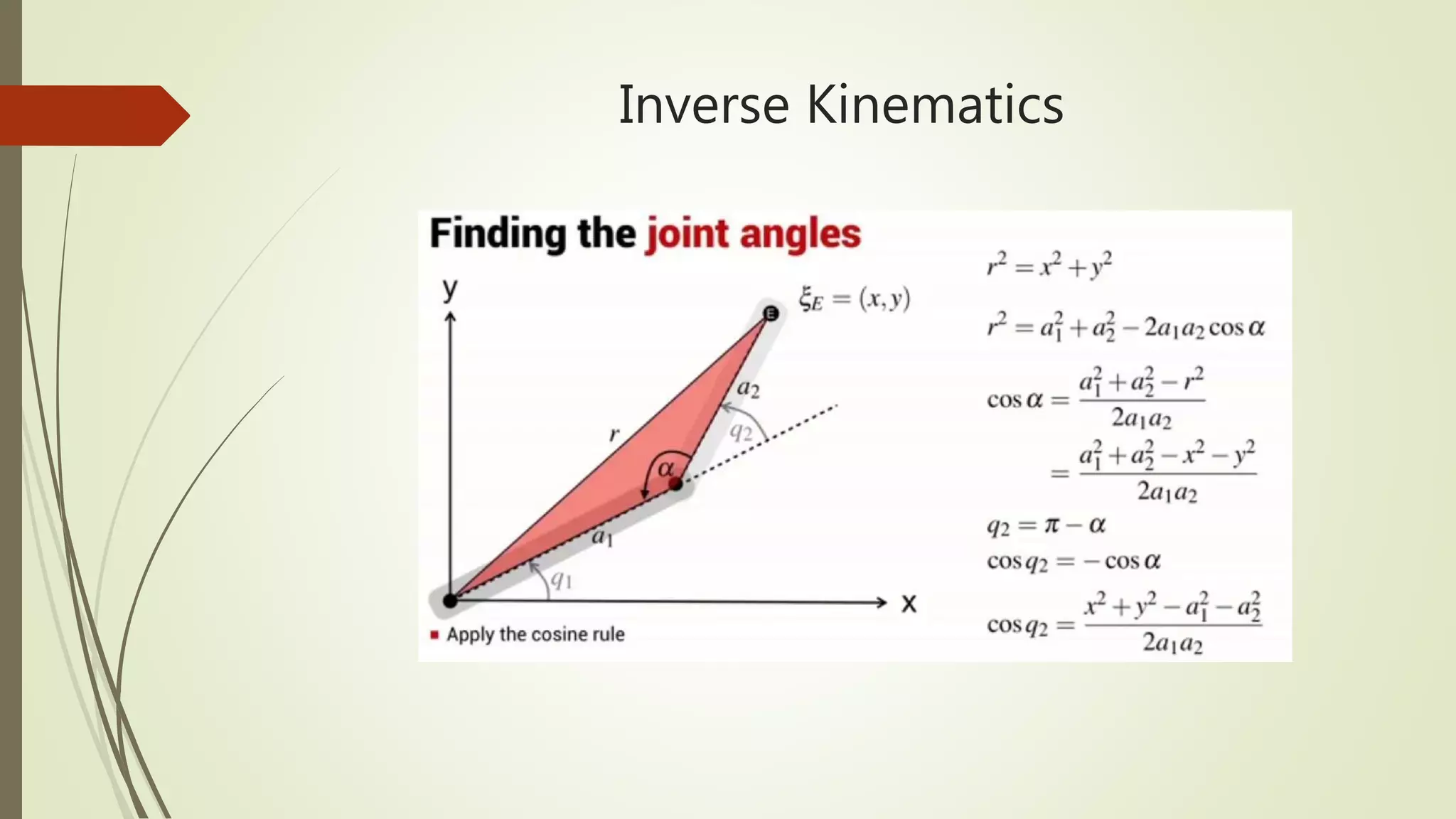
The document discusses forward and inverse kinematics calculations for a planar robot. It provides the dimensions of a 2-link robot and uses MATLAB code to calculate the end effector position and orientation given joint angles. It also presents the concept of inverse kinematics using symbolic math and an example inverse kinematics calculation for a PUMA 560 robot.

1. Robotics Lecture 3
BY: Mahmoud Hussein

2. Revision Forward Kinematics Matlab
 The design of a small new planar robot is shown in the figure below, along with its
dimensions in units of centimeters.
 The robot is shown in its zero angle configuration, and the direction of positive
angular increase is indicated.
 Find the position of the end effector and its orientation when the robot joint angles
are as given by elements of the workspace vector q in units of degrees.
 Return the x-coordinate of the end effector in the workspace variable x in meters,
the y-coordinate of the end effector in y in meters, and the orientation in degrees
in the workspace variable theta.

3. Revision Forward Kinematics Matlab
 % DO NOT MODIFY THE FOLLOWING LINES
 q = [30 -20];
 % Find the pose of the end-effector and store in the variable T.
 T = trot2(30,'deg')*transl2(9,3)*trot2(-20,'deg')*transl2(7,0);
 % Find the x-coordinate in metres and store in the variable x.
 a=T;
 x = a(1,3)/100;
 % Find the y-coordinate in metres and store in the variable y.
 y =a(2,3)/100;
 % Find the orientation angle by examining elements of the % rotation submatrix,
element (1,1) which is equal to cos(theta).
 % Store in the variable theta.
 theta = acosd(a(1,1))

4. Inverse Kinematics

5. Inverse Kinematics

6. Inverse Kinematics

7. Inverse Kinematics

8. Inverse Kinematics

9. Inverse Kinematics

10. Inverse Kinematics

11. Inverse Kinematics

12. Inverse Kinematics

13. Inverse Kinematics

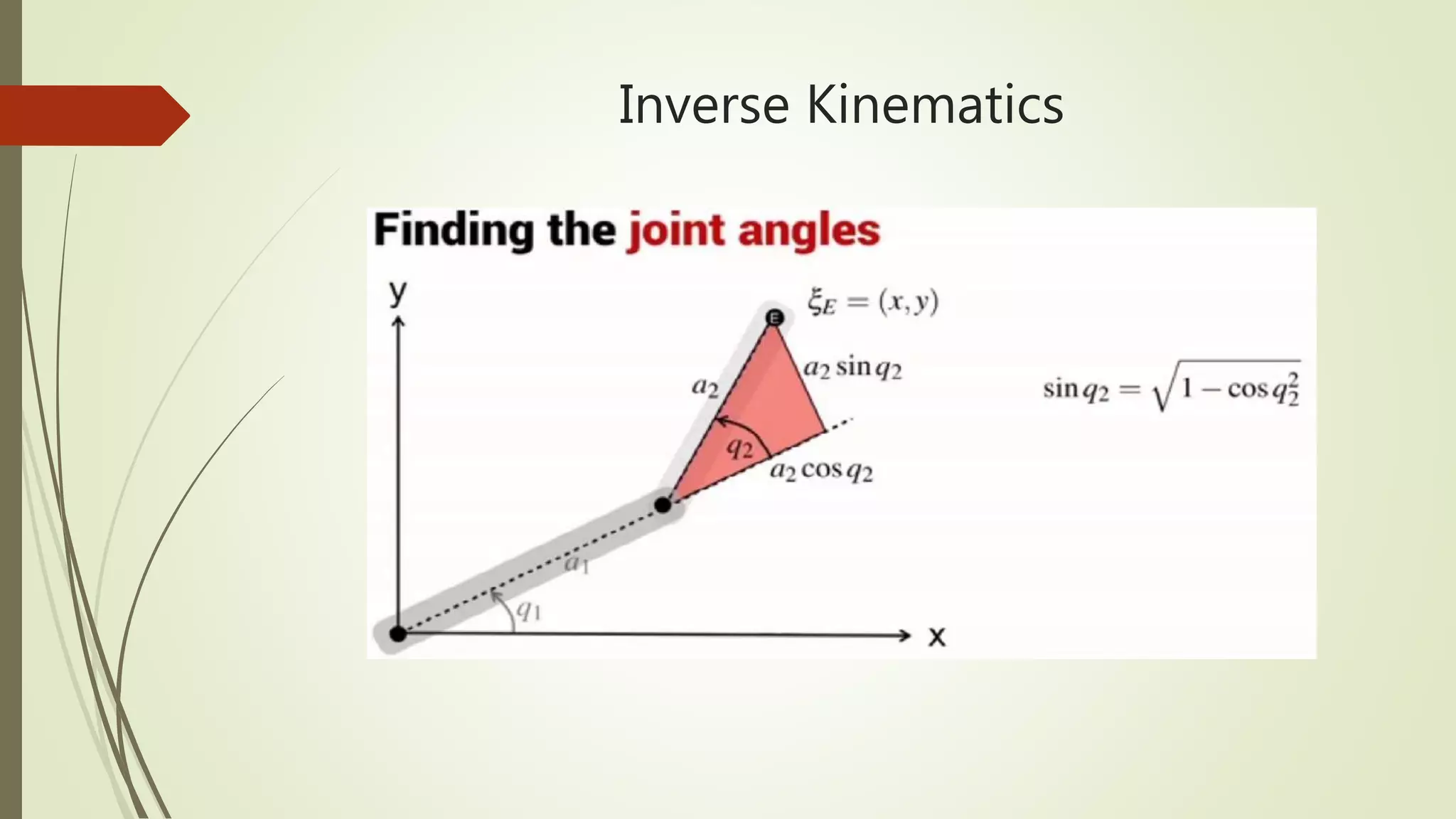
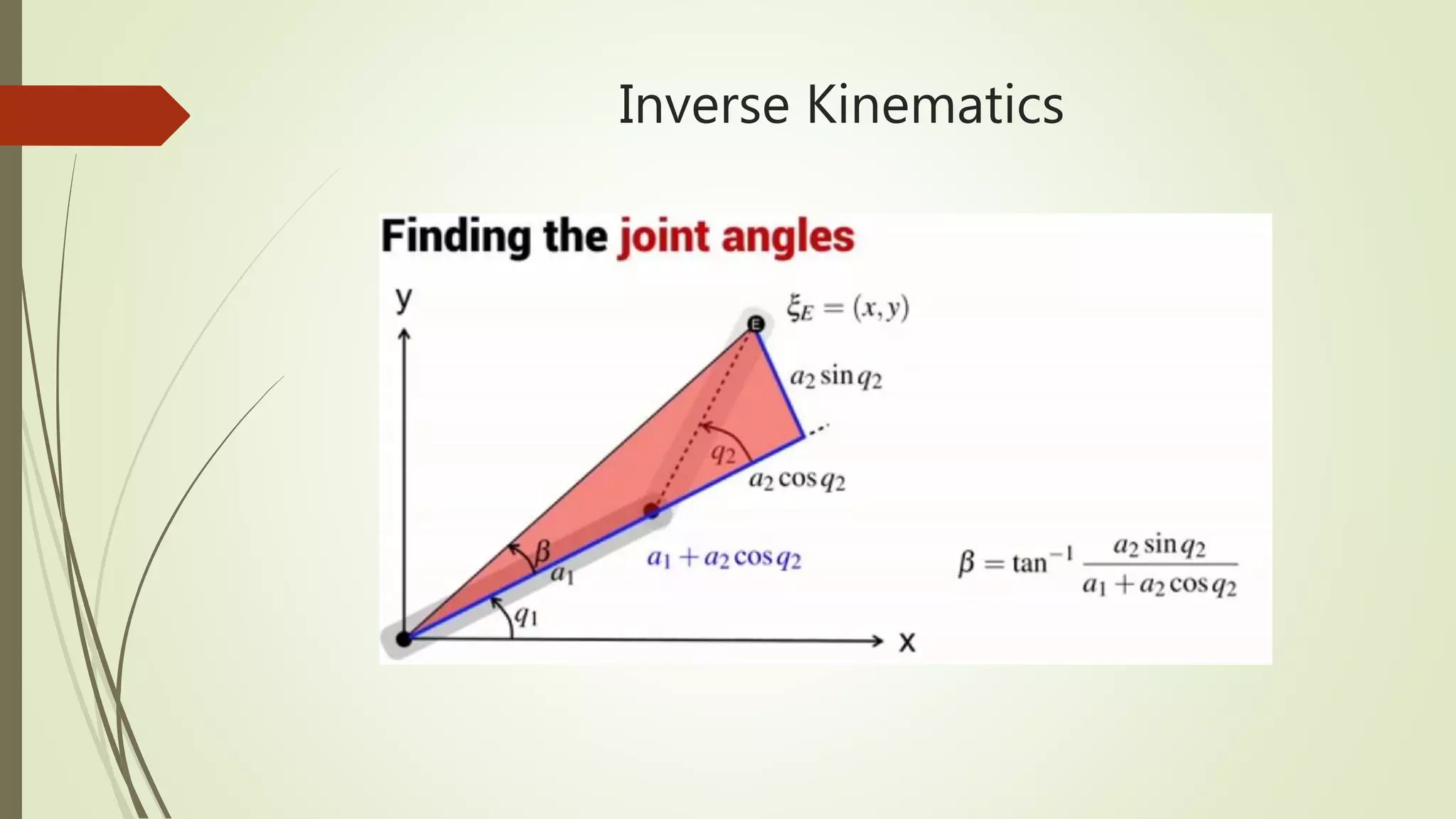
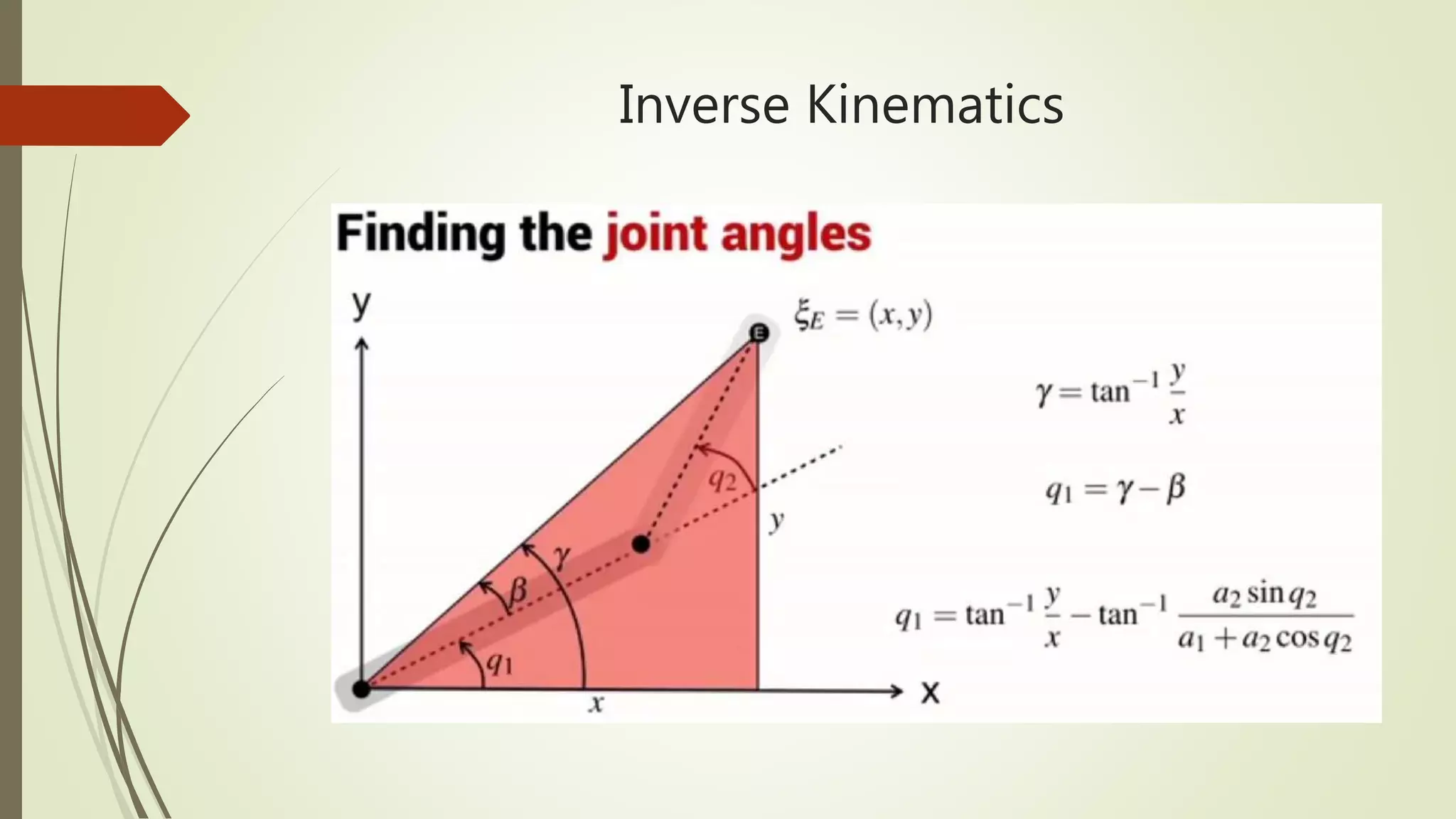
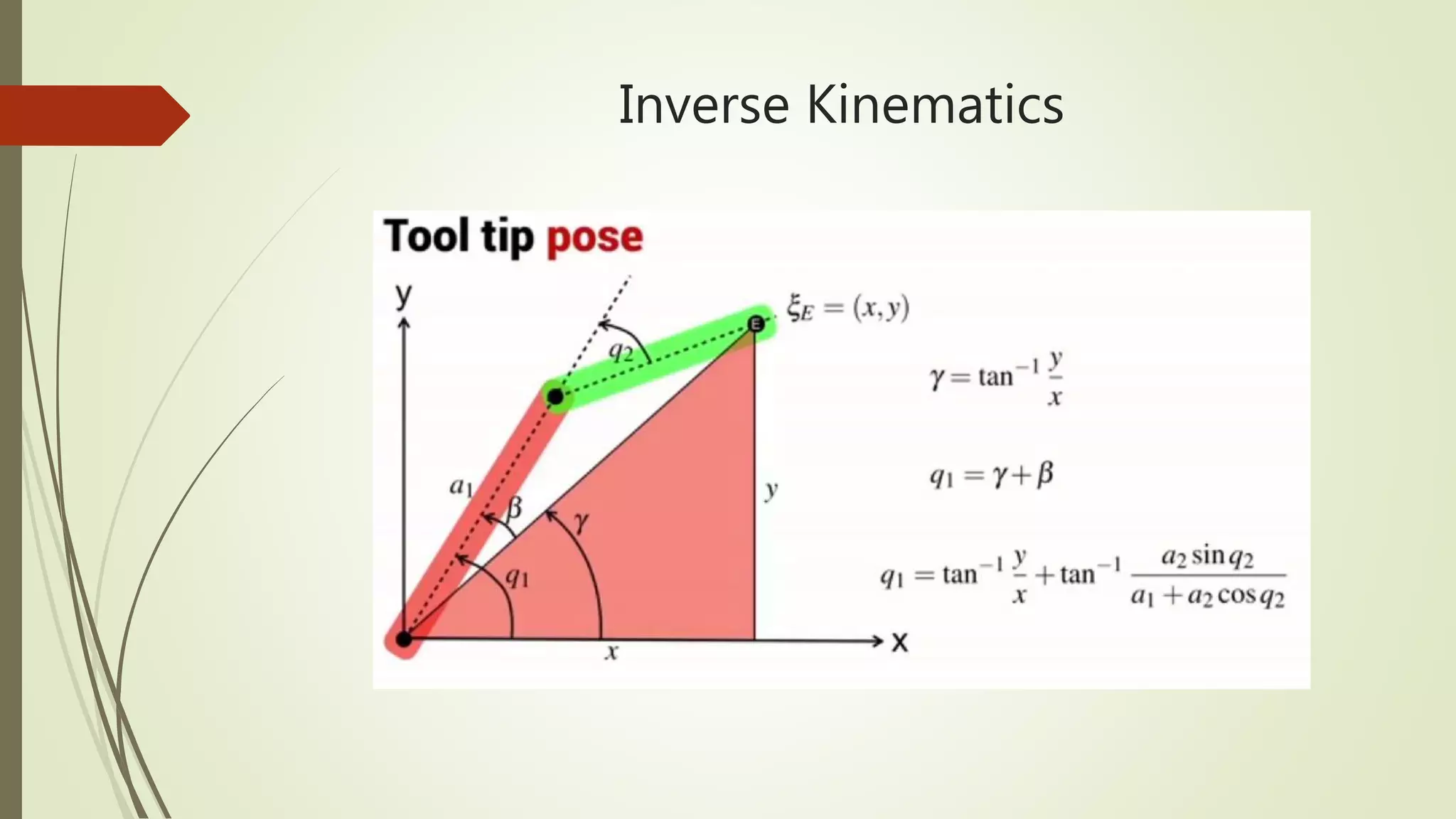
14. Matlab code
 syms a1 a2 a3 a4 q1 q2 q3 q4
 trchain('Rz(q1)Tz(a1)Ry(q2)Tz(a2)Ry(q3)Tz(a3)Ry(q4)Tz(a4)',[q1 q2 q3 q4])
 mdl_puma560
 T = transl(0.6, 0.1, 0) * rpy2tr(0, 180, 0, 'deg')
 q = p560.ikine6s(T)