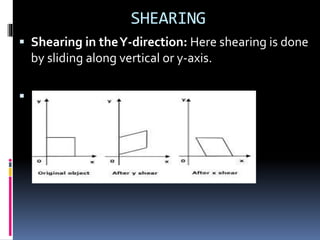
This document discusses 2D transformations in computer graphics, including rotation, reflection, and shearing. It explains rotation using trigonometric equations to express transformed coordinates in terms of an angle, and represents rotation using a rotation matrix. Reflection is described as rotating an object 180 degrees about an axis, and reflection about the x-axis is represented using a matrix. Shearing is defined as a transformation that changes an object's shape by sliding its layers, and shearing matrices for the x and y directions are provided.

1. 2D TRANSFORMATIONS
IN COMPUTER GRAPHICS
VIJAY
SHARMA

2. 2D Transformations
 “Transformations are the operations applied
to geometrical description of an object to
change its position, orientation, or size are
called geometric transformations”.

3. ROTATION
 A two dimensional rotation is applied to an object
by repositioning it along a circular path in the xy
plane.
 Using standard trigonometric equations , we can
express the transformed co-ordinates in terms of Ө
and Φ as
x’ = r cos (Φ+Ө) = r cosΦ cosӨ – r sinΦ sinӨ……(1)
y’ = r sin (Φ+Ө) =r cos Φ sin Ө + r sinΦ cosӨ…….(2)

4. ROTATION
 The original co-ordinates of the point is
x= r cos Φ
y= r sin Φ

5. ROTATION
 By putting the r cosΦ=x and r sinΦ=y in equation (1)
and (2) we get :-
x’=x cos Ө – y sin Ө
y’=x sin Ө + y cos Ө
We can write this equation as,
P’ = P . R
Where R is a rotation matrix and it is given as
R = cosӨ sinӨ
-sinӨ cosӨ

6. REFLECTION
 In this transformation the mirror image of an object
is produced.
 The object is rotated about any axis by 180ᵒ
 So for reflection we need reflection axis, there can
be various cases depending upon the axis chosen for
the reflection.
 Reflection about X axis: To reflect a point P(x,y) to
new position P’(x’,y’) about x-axis use the equation:
x’=x
y’=-y

7. REFLECTION

 Equation can also be represented in matrix form as:
P’=P.R
x’ = 1 0 . x
y’ 0 -1 y

8. SHEARING
 It is transformation which changes the shape of
object.The sliding of layers of object occur.The
shear can be in one direction or in two directions.
 Shearing in the X-direction: In this horizontal
shearing sliding of layers occur.The homogeneous
matrix for shearing in the x-direction is shown on
below:
1 0 0
Shₓ 1 0
0 0 1

9. SHEARING
 Shearing in theY-direction: Here shearing is done
by sliding along vertical or y-axis.
