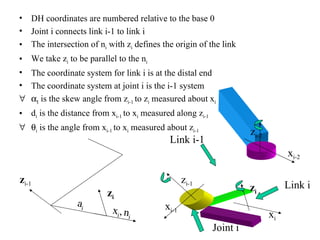
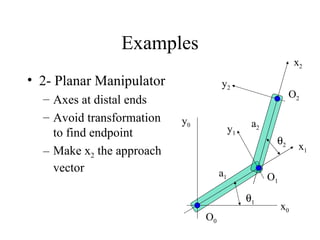
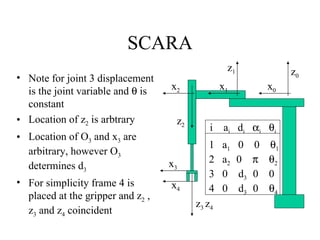
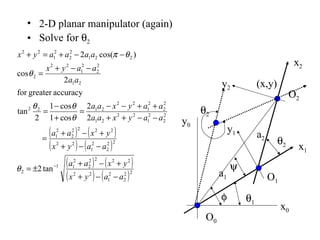
The document discusses forward kinematics, which is finding the position and orientation of the end effector given the joint angles of a robot. It covers different types of robot joints and configurations. It introduces the Denavit-Hartenberg coordinate system for defining the relationship between successive links of a robot. The document also discusses forward kinematic calculations, inverse kinematics, robot workspaces, and trajectory planning.

1. Forward Kinematics “ Finding the end effector given the joint angles”

2. Types of robot joints Rotary Angle  about z axis Prismatic/sliding Linear displacement d along axis of joint z Hooke (2-D Rotary) 2-D of freedom described by Yaw and Pitch Spherical Described by 3 rotation axes (wrist & shoulder)

3. Robot configurations Cartesian(inspection) 3 Prismatic joints SCARA (pick and place) Min 3 axes (Z axis and 2+ rotary joints) Spherical Wrist Most common type 6-D freedom hooke shoulder, rotary elbow and roll-pitch-roll wrist …

4. Setting up the coordinate system: Denavit-Hartenberg Coordinates Key basis for DH coordinates There is only one normal between two lines in space Except: Parallel lines and intersecting lines (common normal has zero length) Suppose there are two joint axes z i and z i-1

5. DH coordinates are numbered relative to the base 0 Joint i connects link i-1 to link i The intersection of n i with z i defines the origin of the link We take z i to be parallel to the n i The coordinate system for link i is at the distal end The coordinate system at joint i is the i-1 system  I is the skew angle from z i-1 to z i measured about x i d i is the distance from x i-1 to x i measured along z i-1  i is the angle from x i-1 to x i measured about z i-1 x i-2 z i-1 x i-1 x i z i-2 z i Joint i Link i Link i-1 a i z i z i-1 x i , n i

6. Parallel or intersecting axes When neighbouring axes intersect a i =0  n i  =0 Arbitrary choice x i  n i or –n i For Parallel axes Chose x i that intersects x i-1 at O i-1 (prefered) Chose x i that intersects x i+1 at O i+1 In these cases DH parameters are very sensitive to small changes in alignment An alternative is the Hayati coordinates

7. Examples 2- Planar Manipulator Axes at distal ends Avoid transformation to find endpoint Make x 2 the approach vector  2  1 a 1 a 2 O 2 O 1 O 0 x 1 x 0 x 2 y 1 y 2 y 0

8. SCARA Note for joint 3 displacement is the joint variable and  is constant Location of z 2 is arbtrary Location of O 3 and x 3 are arbitrary, however O 3 determines d 3 For simplicity frame 4 is placed at the gripper and z 2 , z 3 and z 4 coincident z 0 x 0 z 1 x 1 x 2 z 2 x 3 x 4 z 3 z 4 i a i d i  i  i 1 a 1 0 0  1 2 a 2 0   2 3 0 d 3 0 0 4 0 d 3 0  4

9. Forward Kinematics Link Coordinate Transform From link i to link i-1of the 2-d planar robot Rotate about the z i-1 axis by  i , then about the x i axis by  i .

10. Forward Kinematics Translational component referenced to axes i-1 Homogeneous transform i-1 T i from frame i to frame i-1

11. Relating any two link frames By composition of intervening frames we can link any two frames For efficiency we normally decompose the frames into separate Rotations and Translation components

12. Forward Kinematic computations Aim: find the position and orientation of the last frame, n, wrt the base frame 0 Sometimes additional frames are added at the beginning or end Vision systems Tools or object which are picked up Once an object is grasped the its kinematics are constant and for practical purposes can be considered part of the last link.

13. Kinematic Calibration Set during Manufacture Wear, error, etc… Kinematic callibration schemes Measurement Experimental Tool Transform Most objects geometric and known Vision system

14. Inverse Kinmatics (IK) “ Given a goal position find the joint angles for the robot arm”

15. Inverse Kinematics IK generally harder than FK Sometimes no analytical solution Sometimes multiple solutions Redundant manipulators Sometimes no solution Outside workspace

16. 2-D planar manipulator (again) Solve for  2 Two solutions: elbow up & elbow down  2  1 a 1 a 2 O 2 O 1 O 0 x 1 x 0 x 2 y 1 y 2 y 0   (x,y)  2

17. Given  2 find  1 Note that there are two answers for  1 based on elbow up or down 3-DOF of freedom robot arms Most robots are made of two interconnected 3-DOF arms Elbow joint (position wrist in space) Wrist joint (orient object/tool in space)

18. Workspaces Workspace limitations depend on Joint limits Presence of obstacles Holes: doughnut shaped WS Voids: empty space in WS Total or Reachable Workspace Primary WS: points reachable in all Orientations Secondary WS: total -primary

19. Trajectory Planning Path Planning

20. Trajectory planning Start to Goal avoiding obstacles along the way Joint space easiest because no IK But end effector pose is not controlled Cartesian space planning is easier but IK must be solved

21. Joint Space Trajectories Cubic Trajectories 4 coefficients Satisfy position and velocity constraits For a joint variable q i

22. Polynomials for joint position and velocity The a i coeff. have to be related to the end point constraits

23. This allows us to determine a 2 and a 3 Example 0 100 -20 10

24. Linear segments with parabolic bends We want the middle part of the trajectory to have a constant velocity V Ramp up Linear segment Ramp down

25. Ramp Up A quadratic requires 3 constraits 2 for the start and 1 for const velocity at the end

26. Linear Section Given constant velocity V, which we ramp up to in a unknown time t b , we can find a 2 in terms of t b

27. Similarly the end position can be show to be