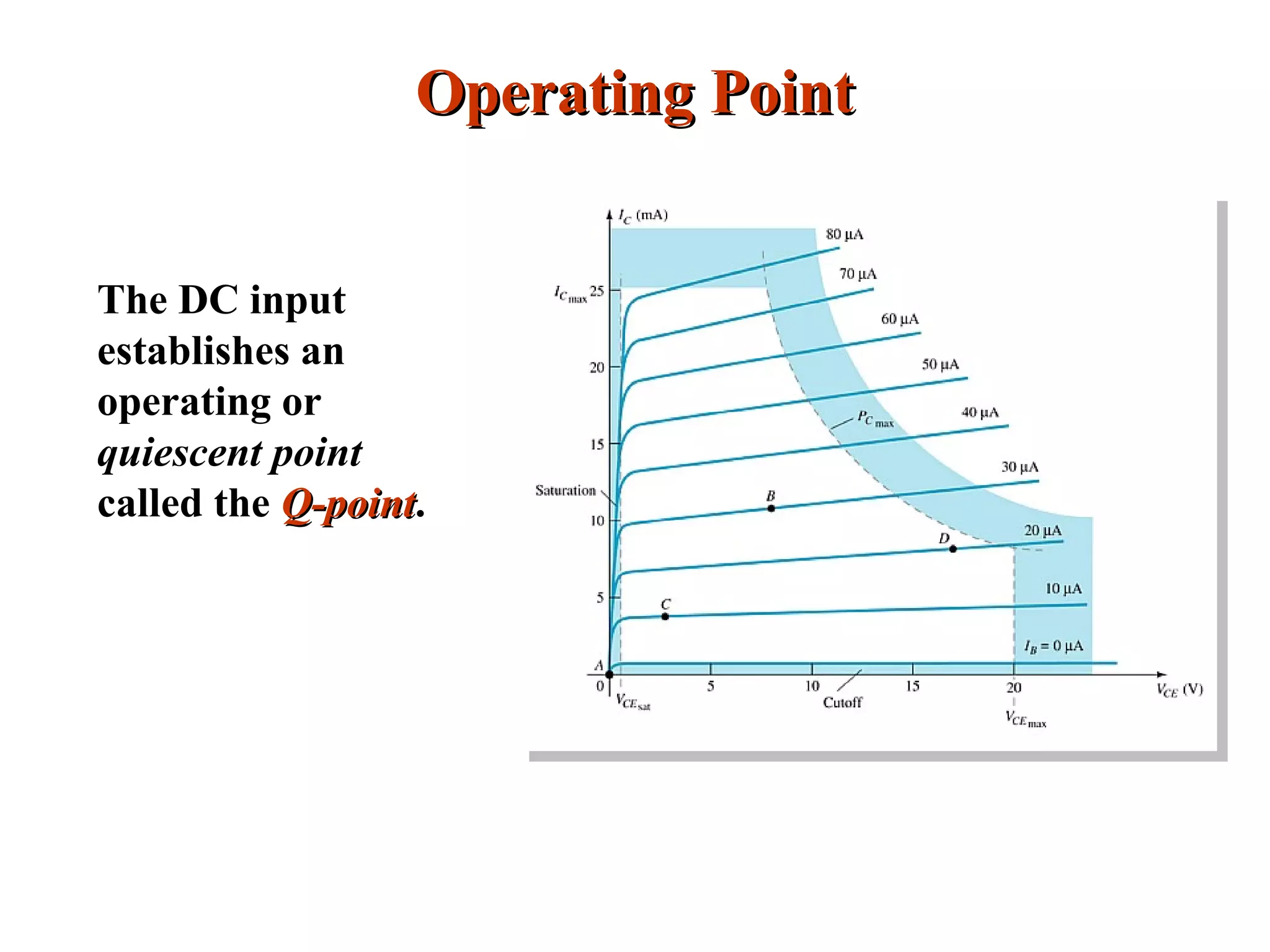
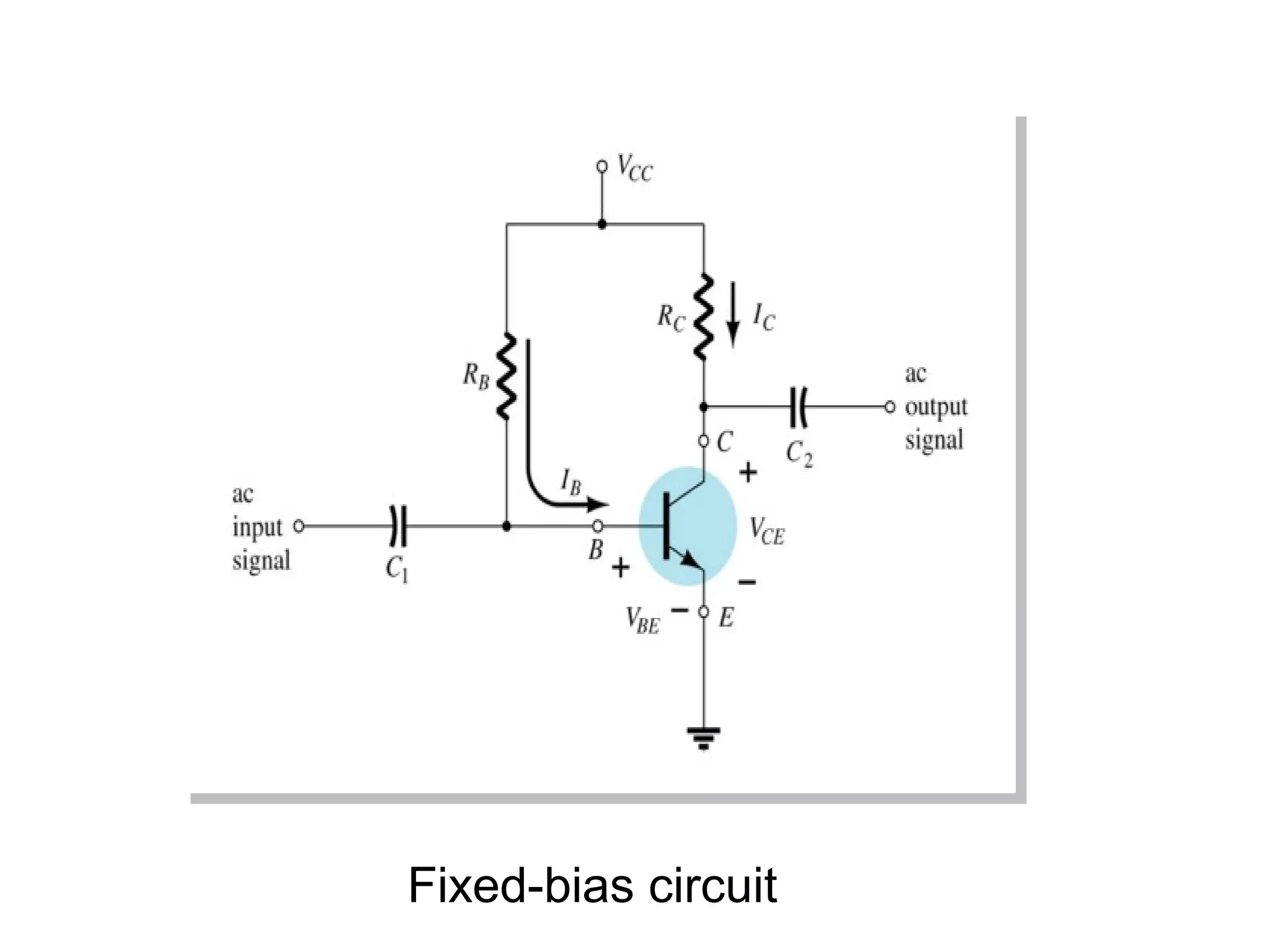
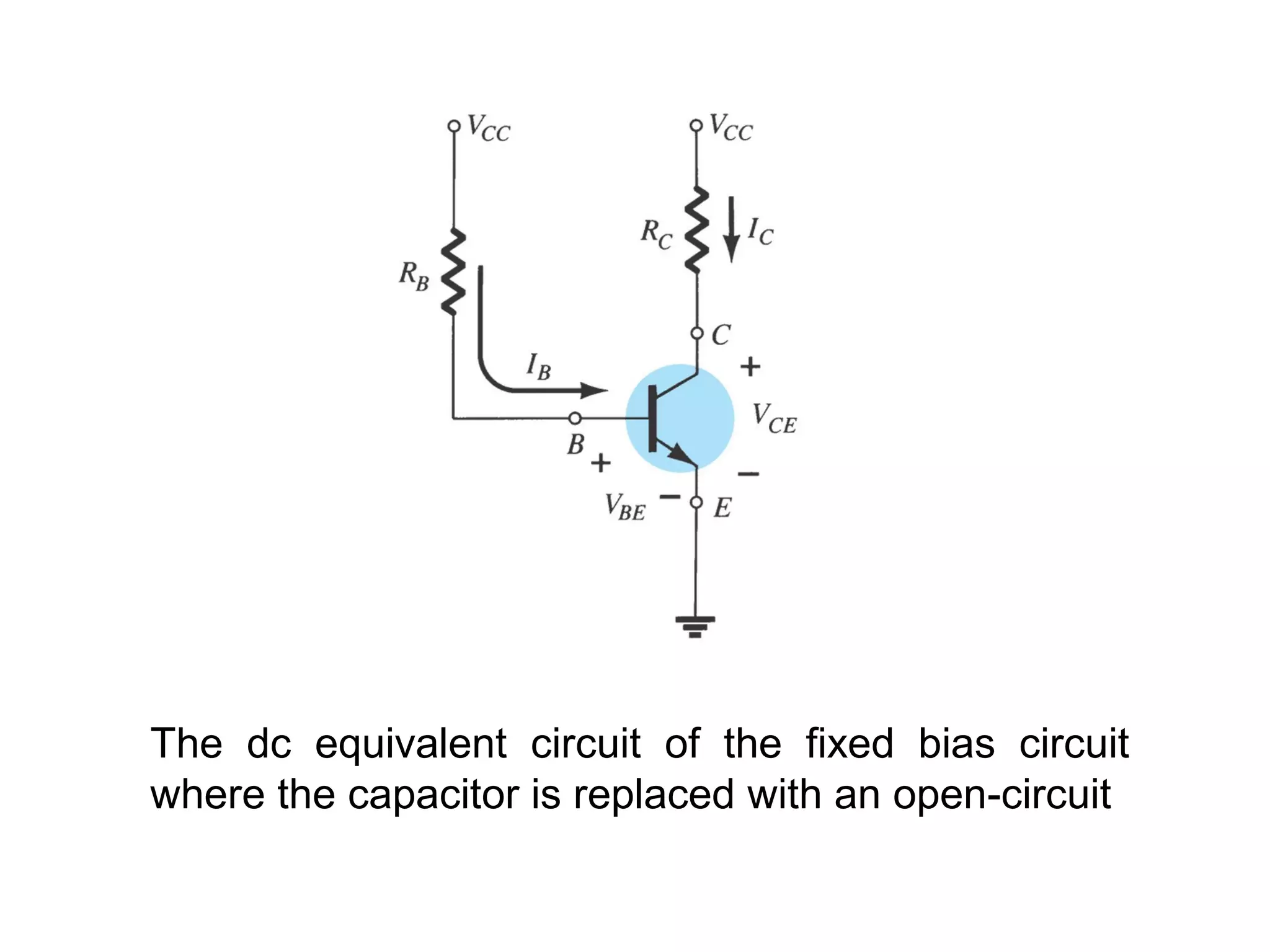
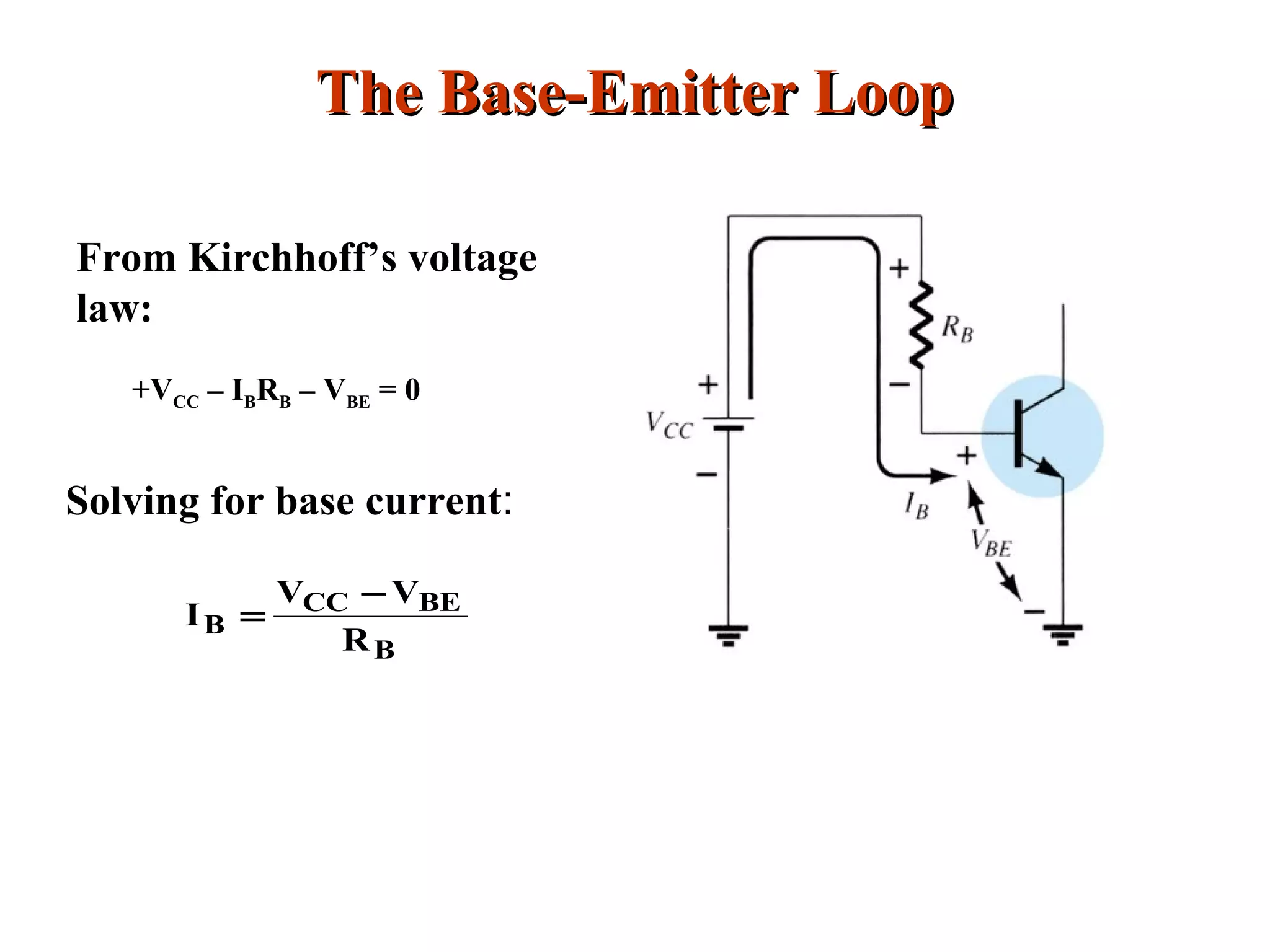
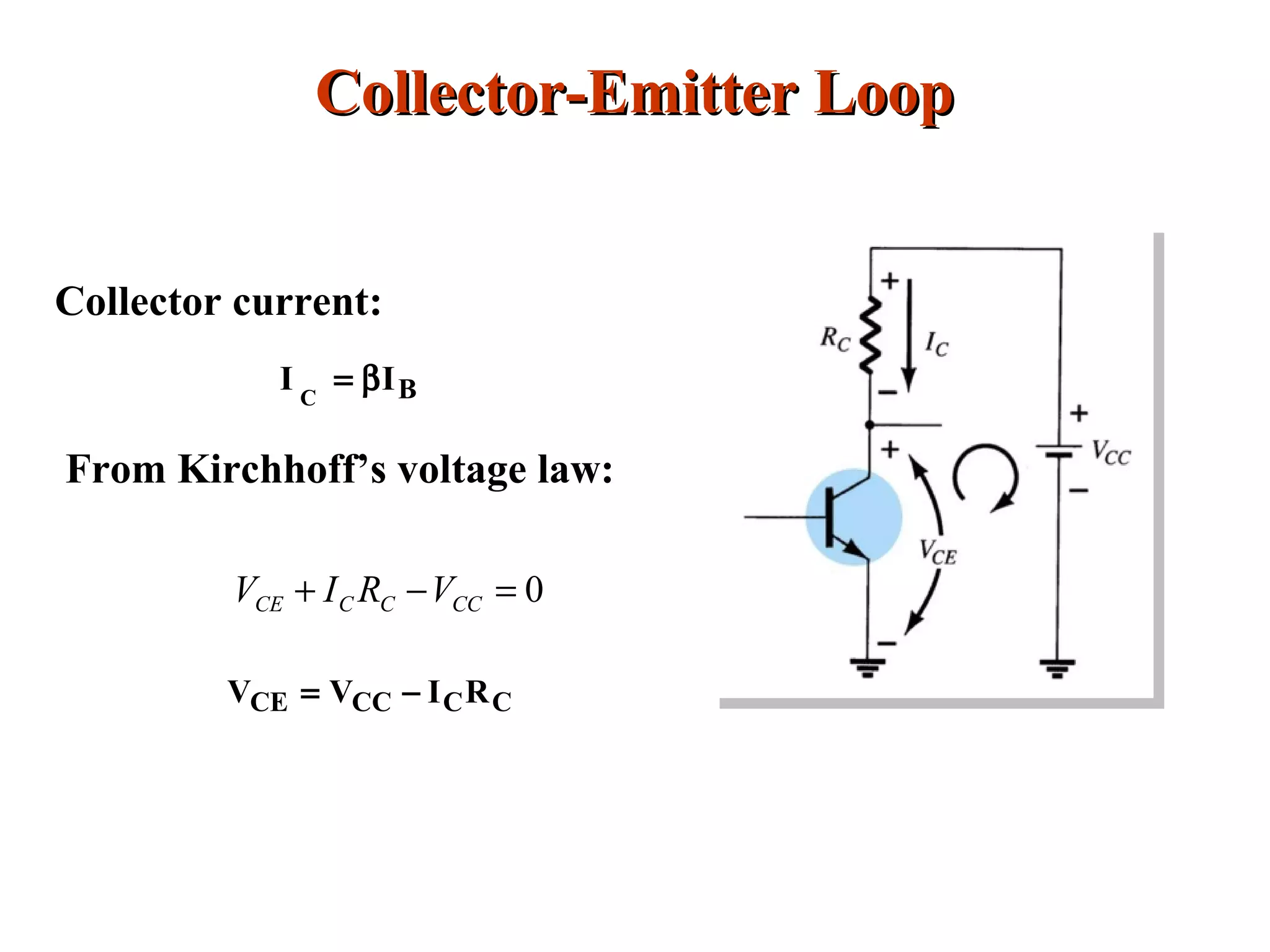
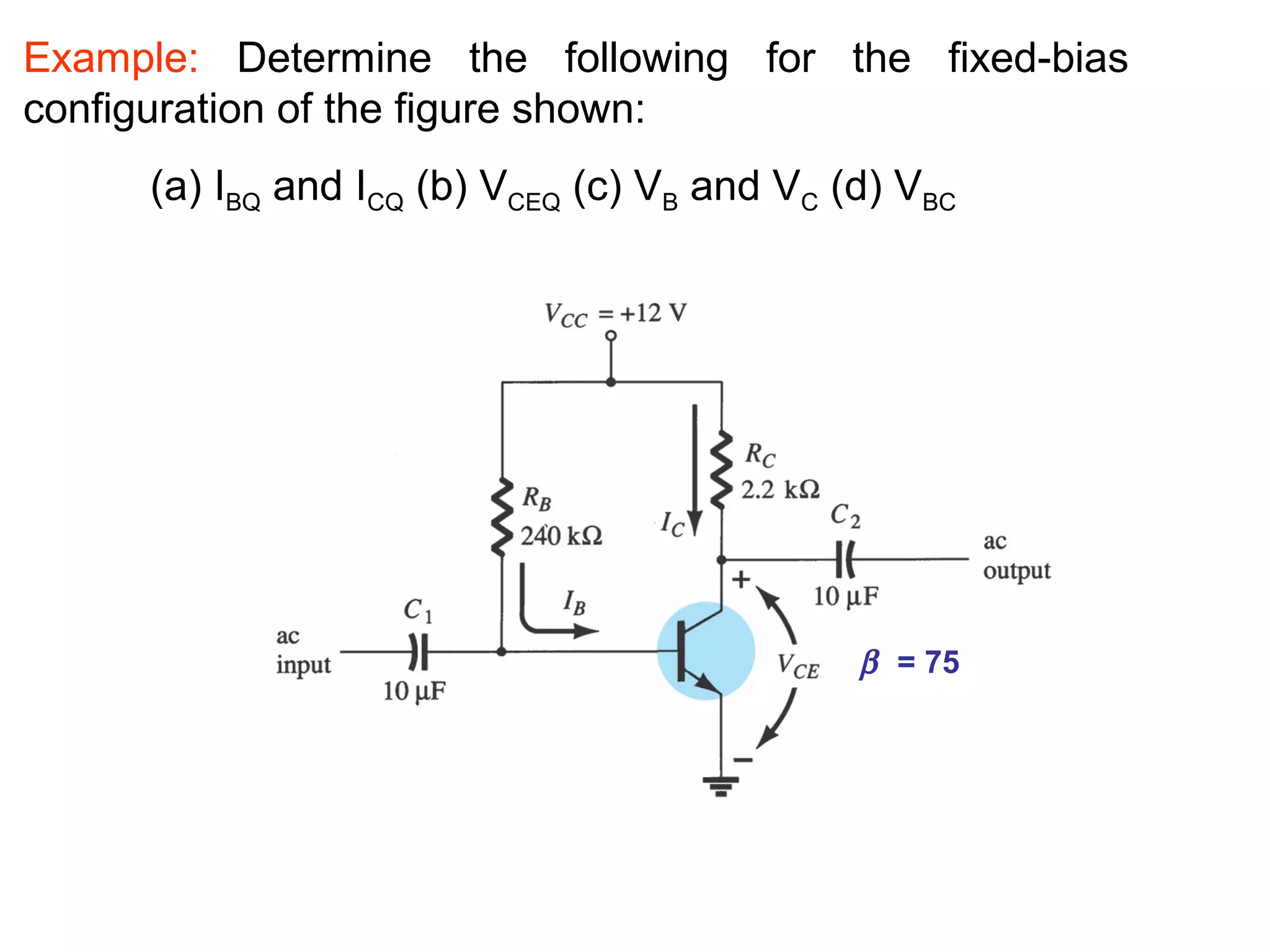
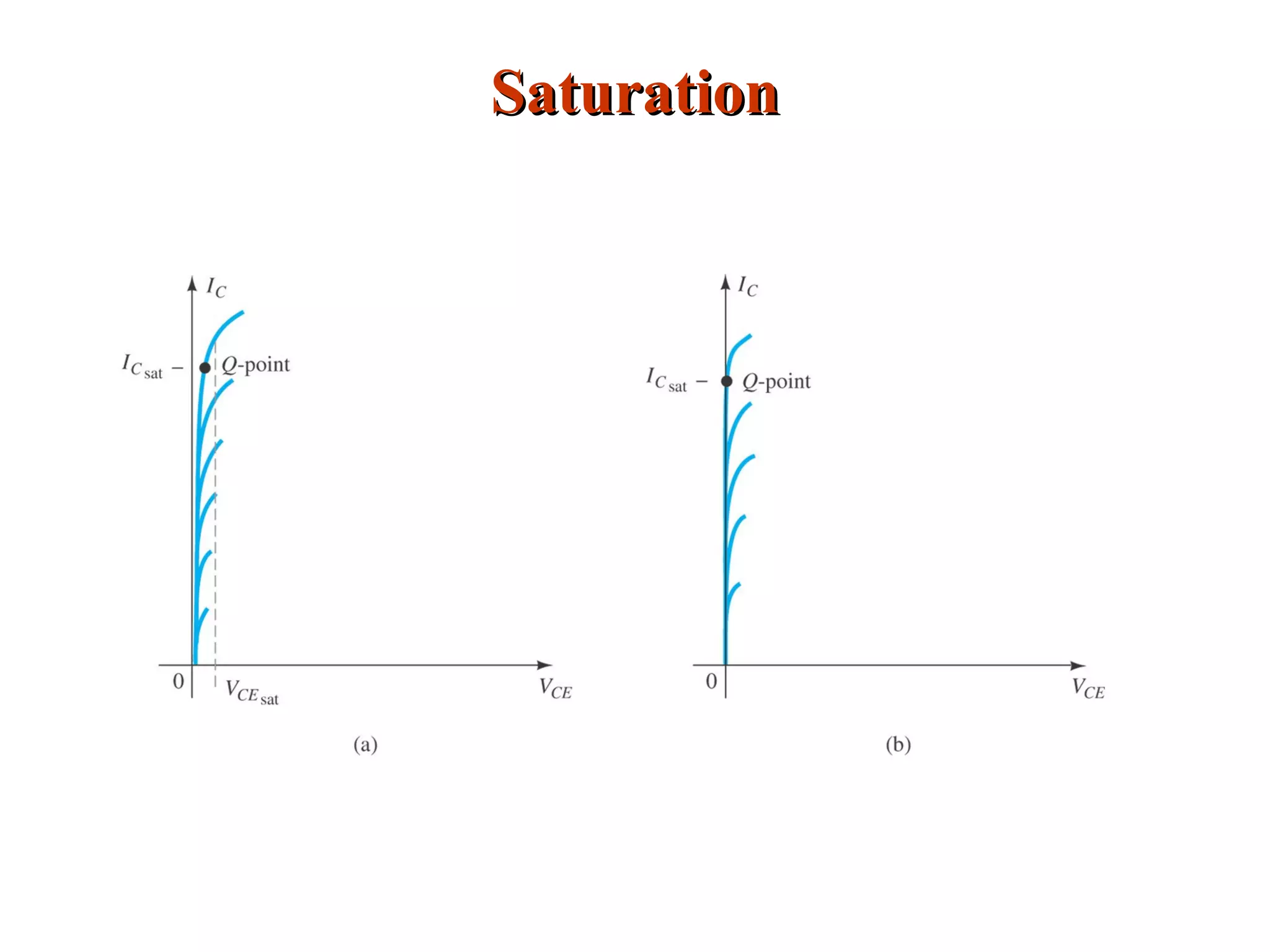
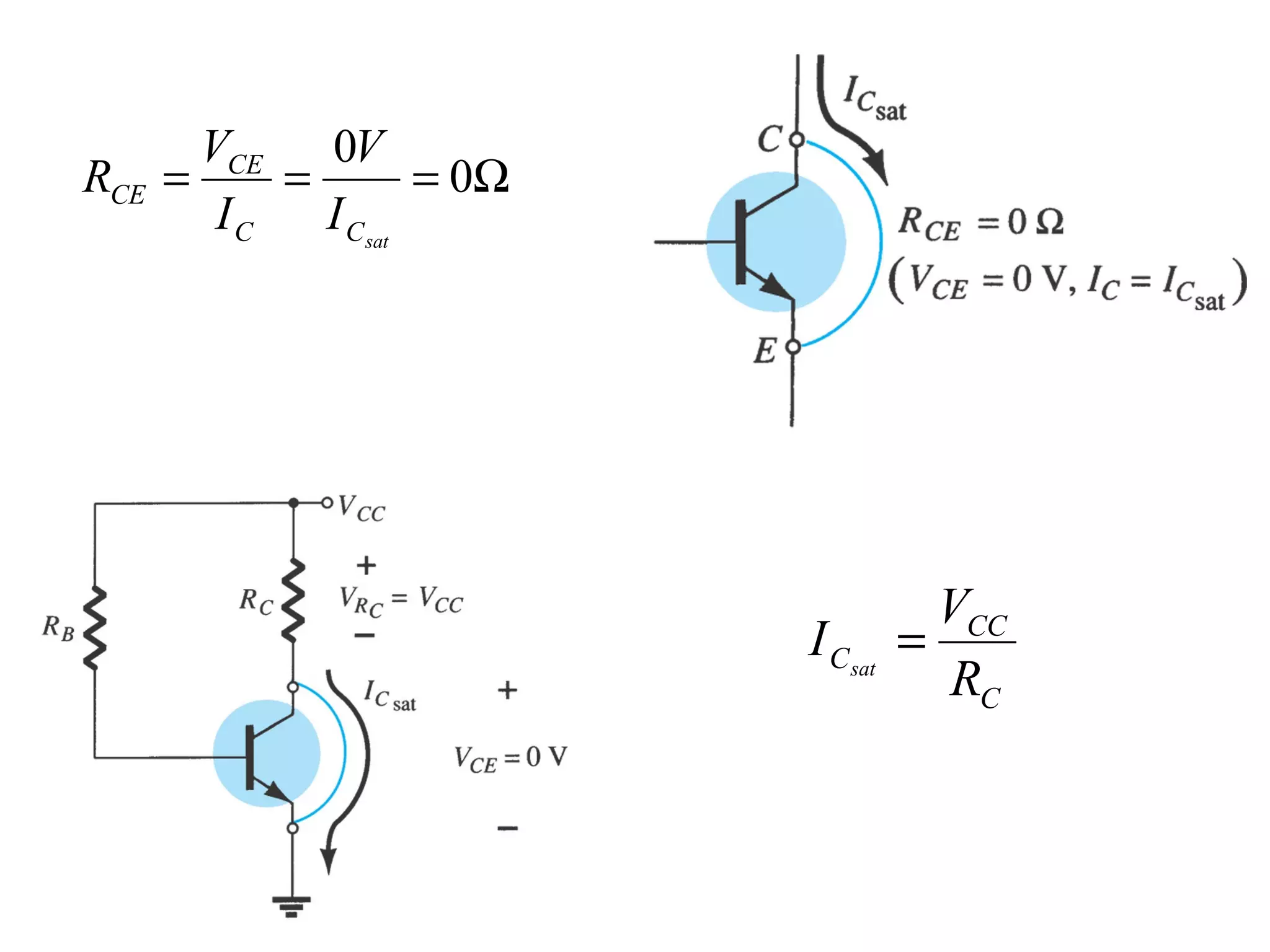
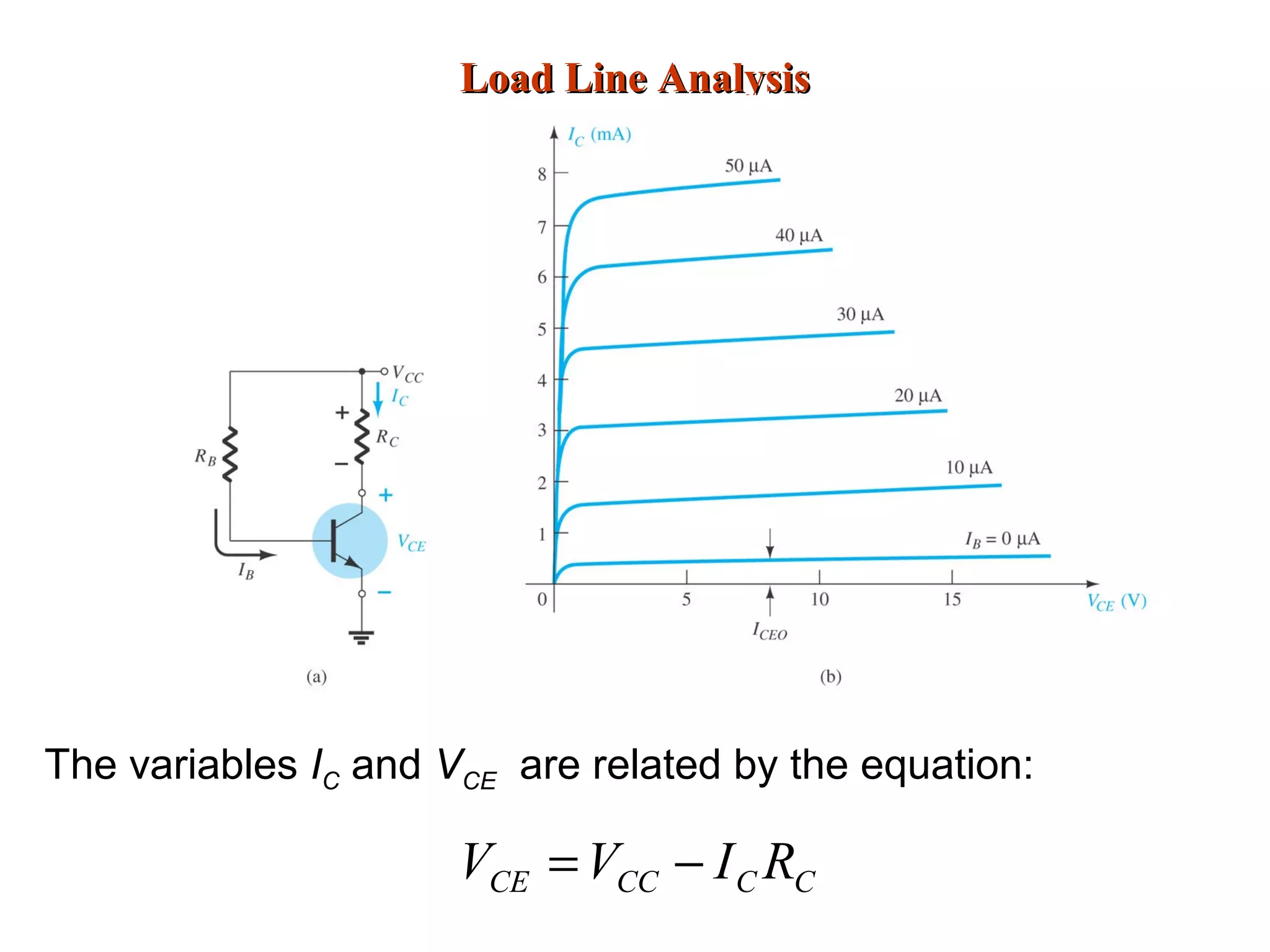
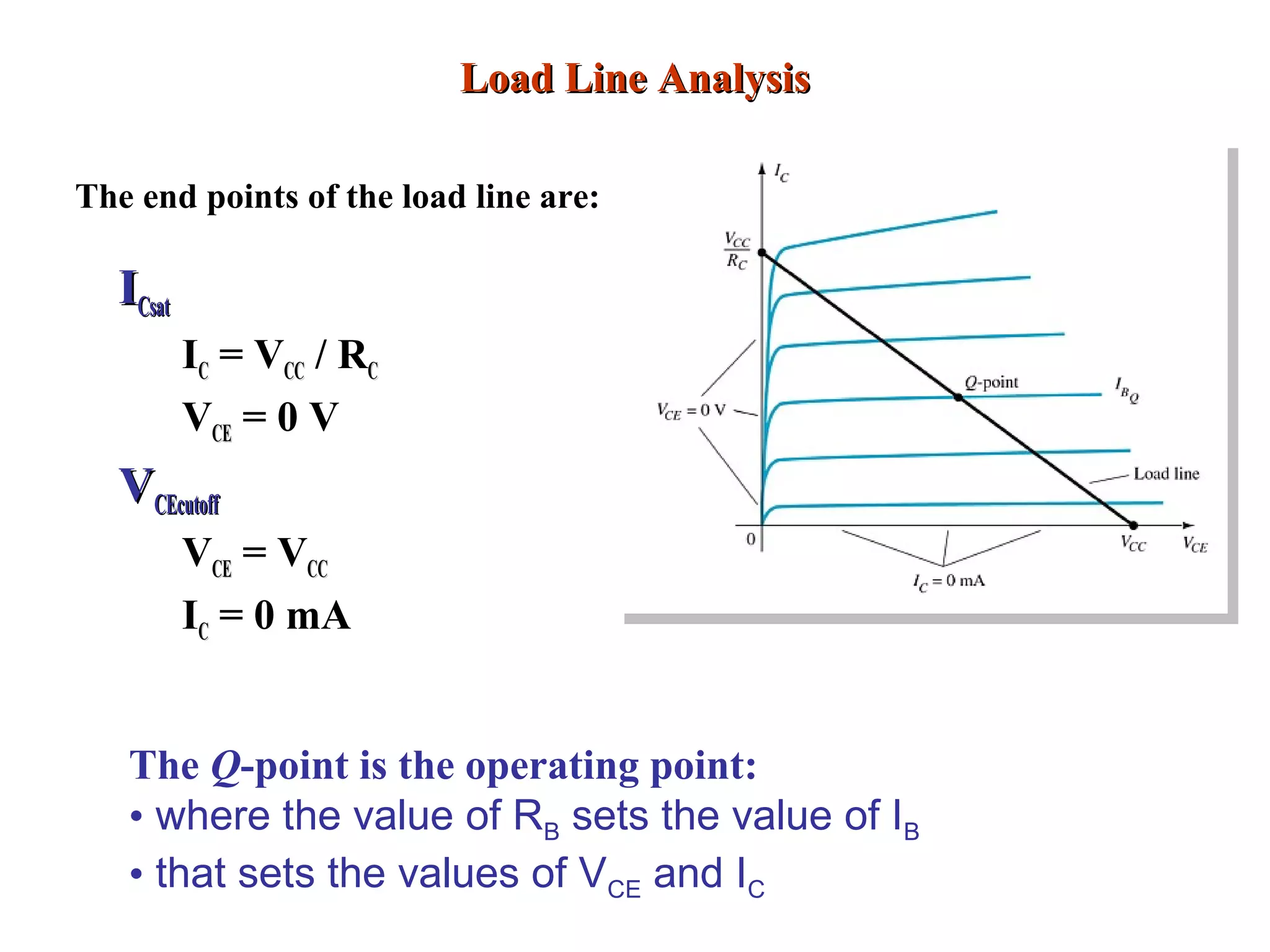
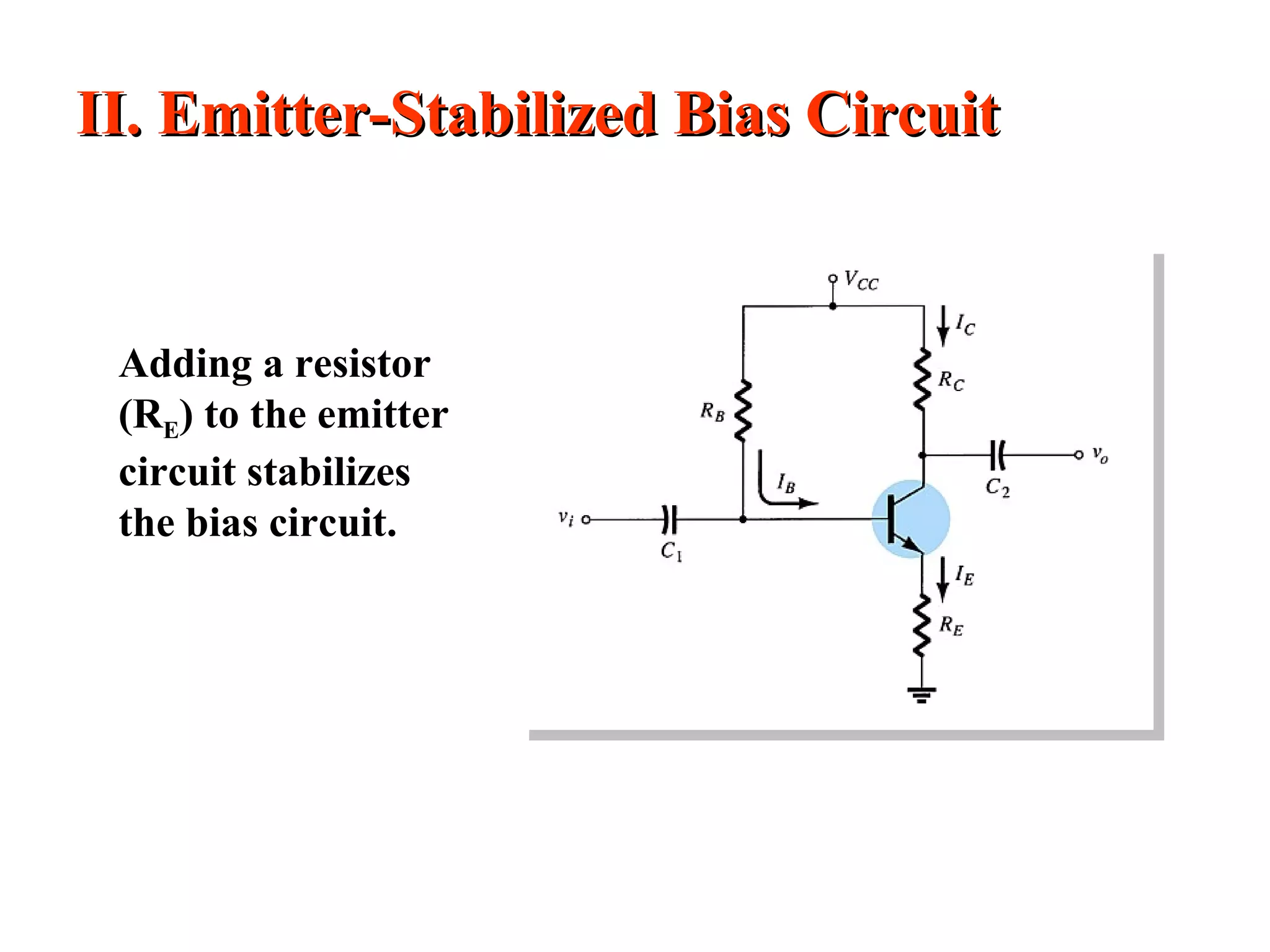
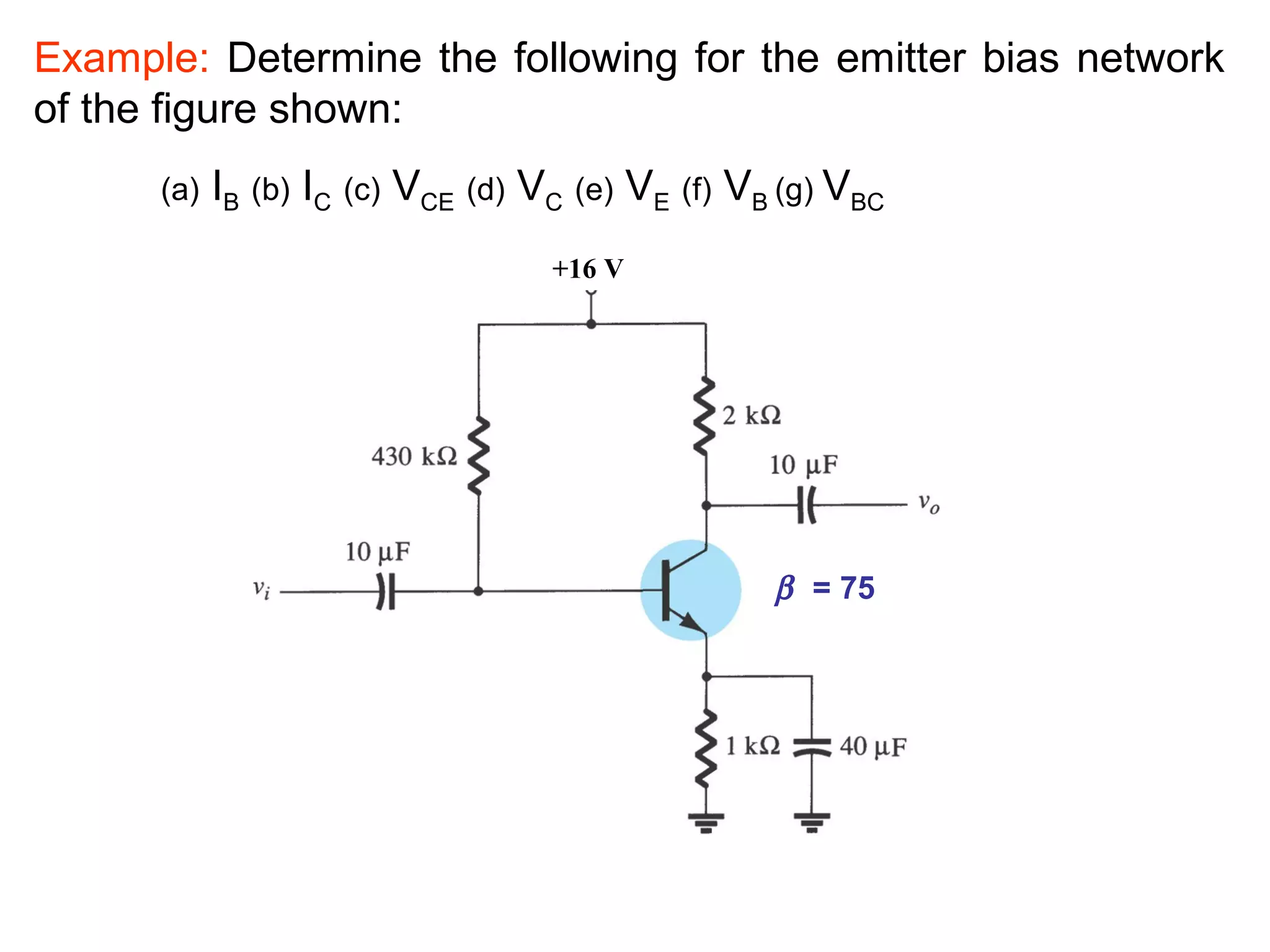
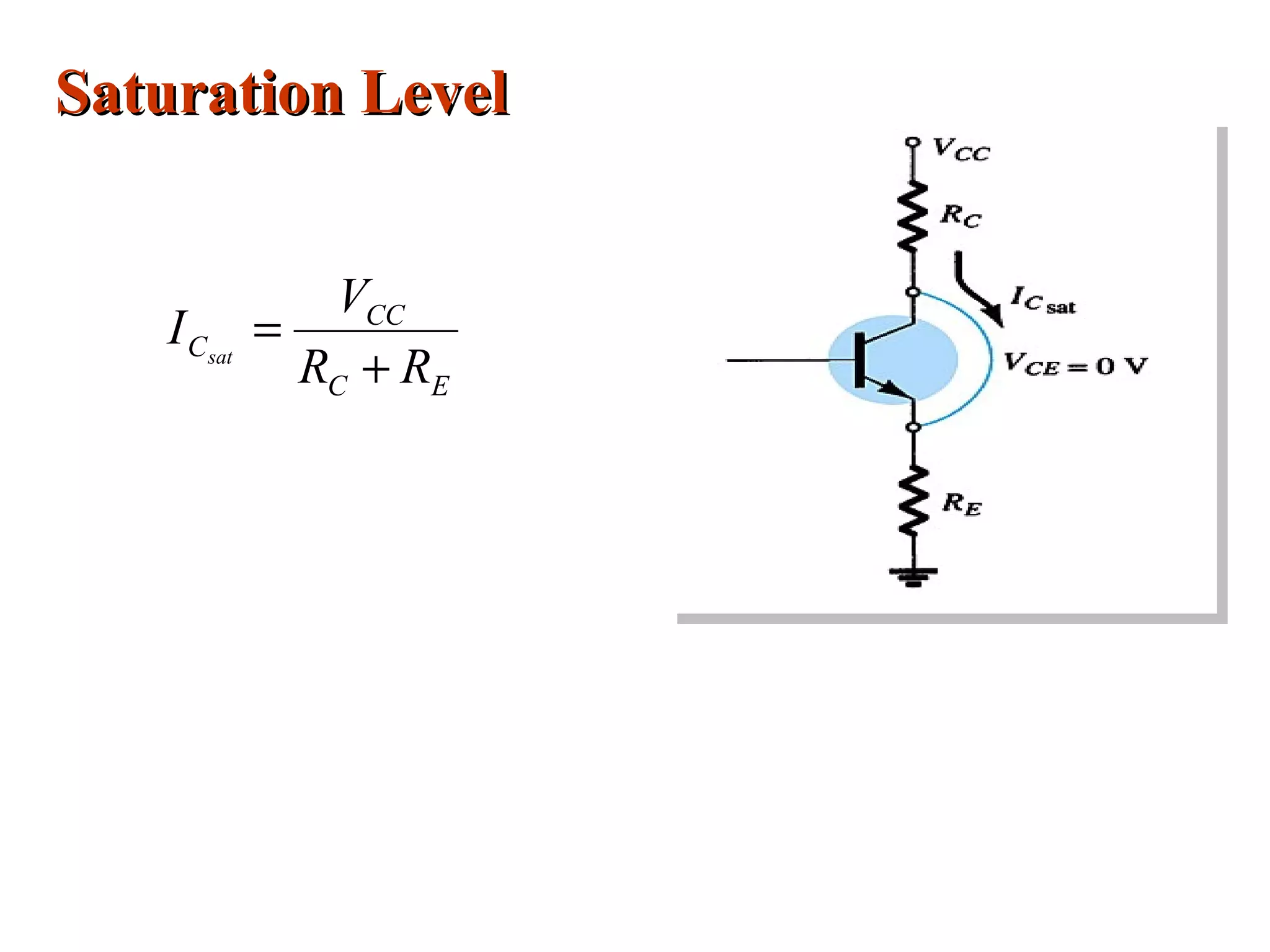
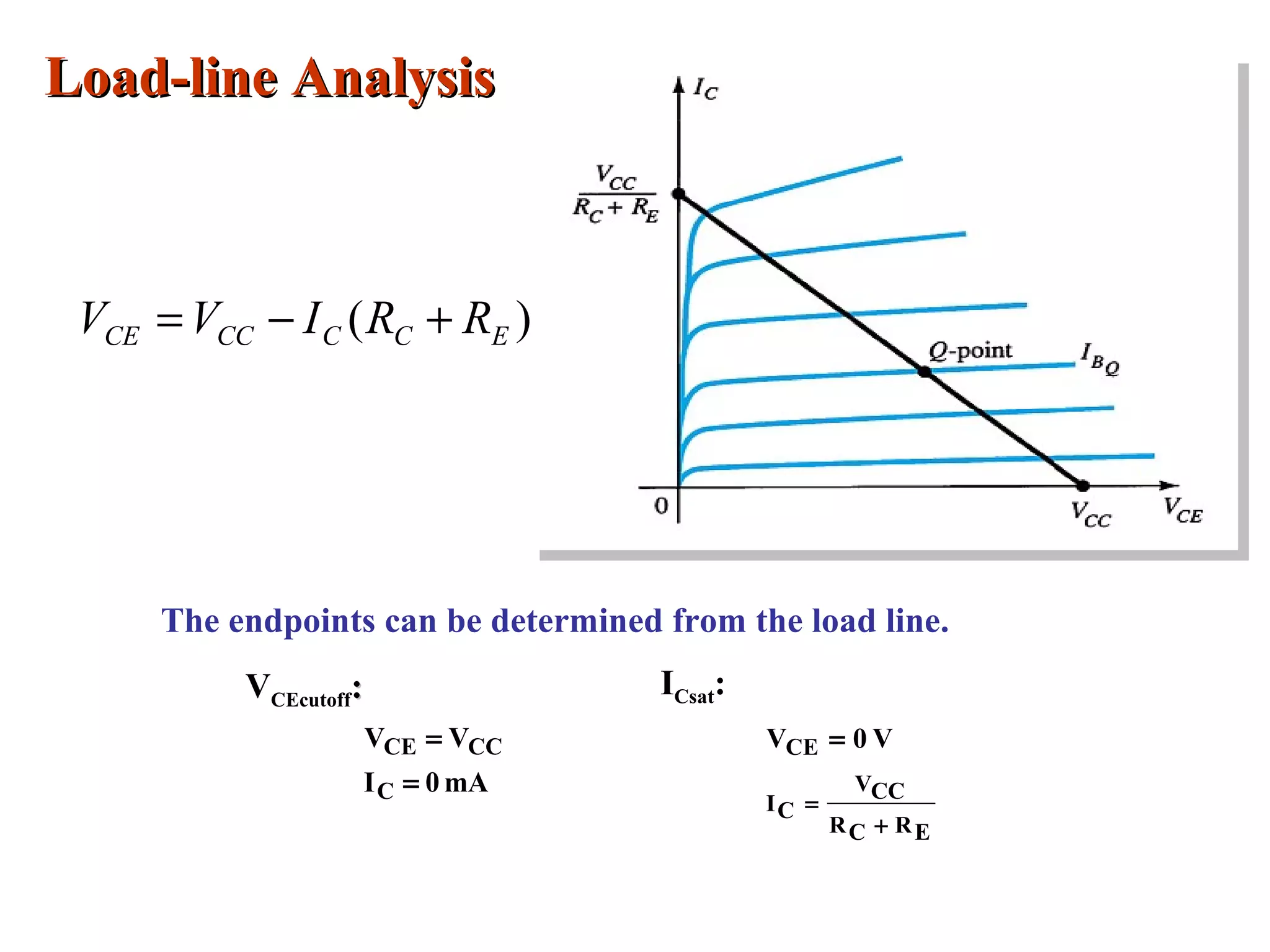
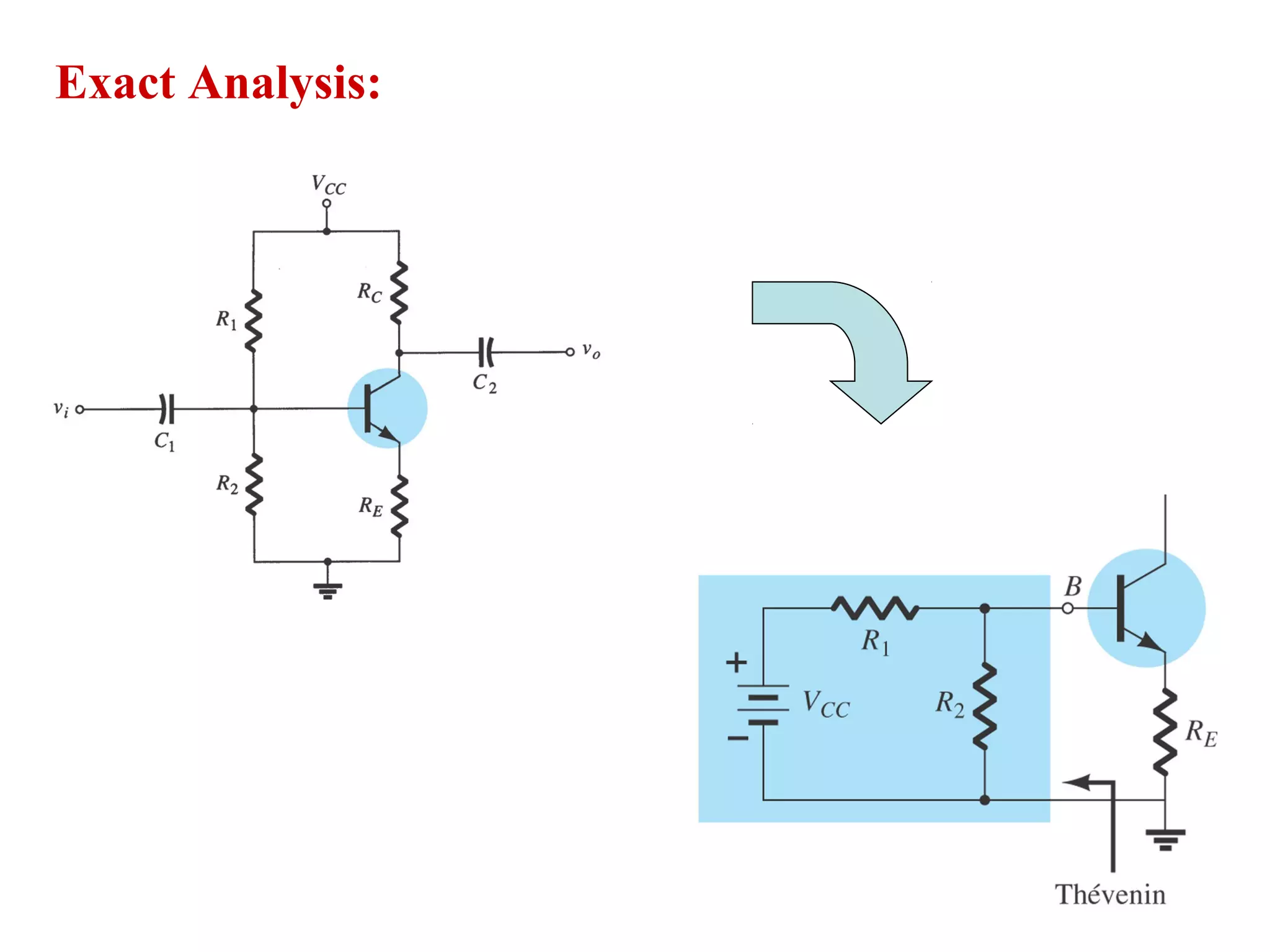
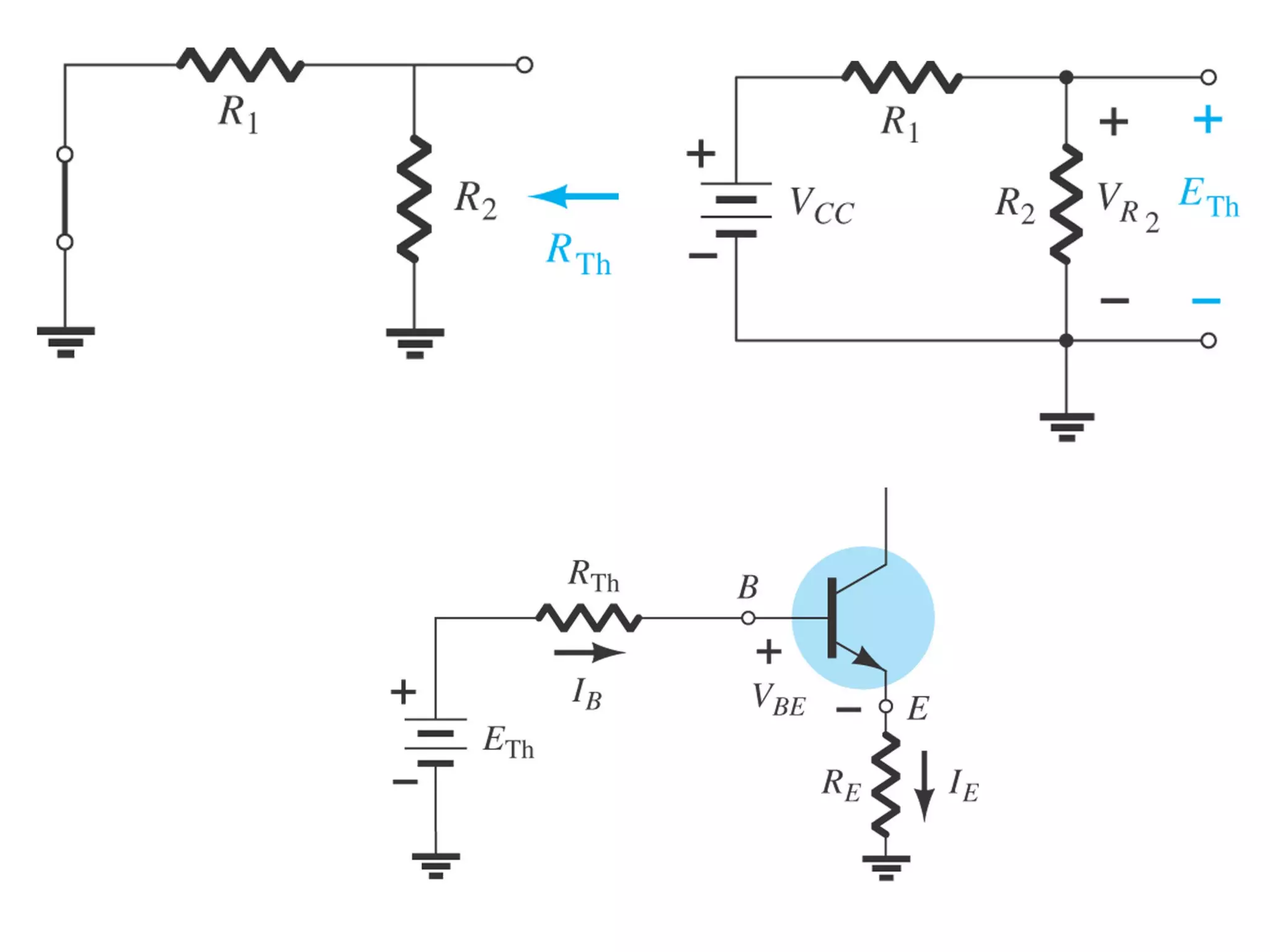
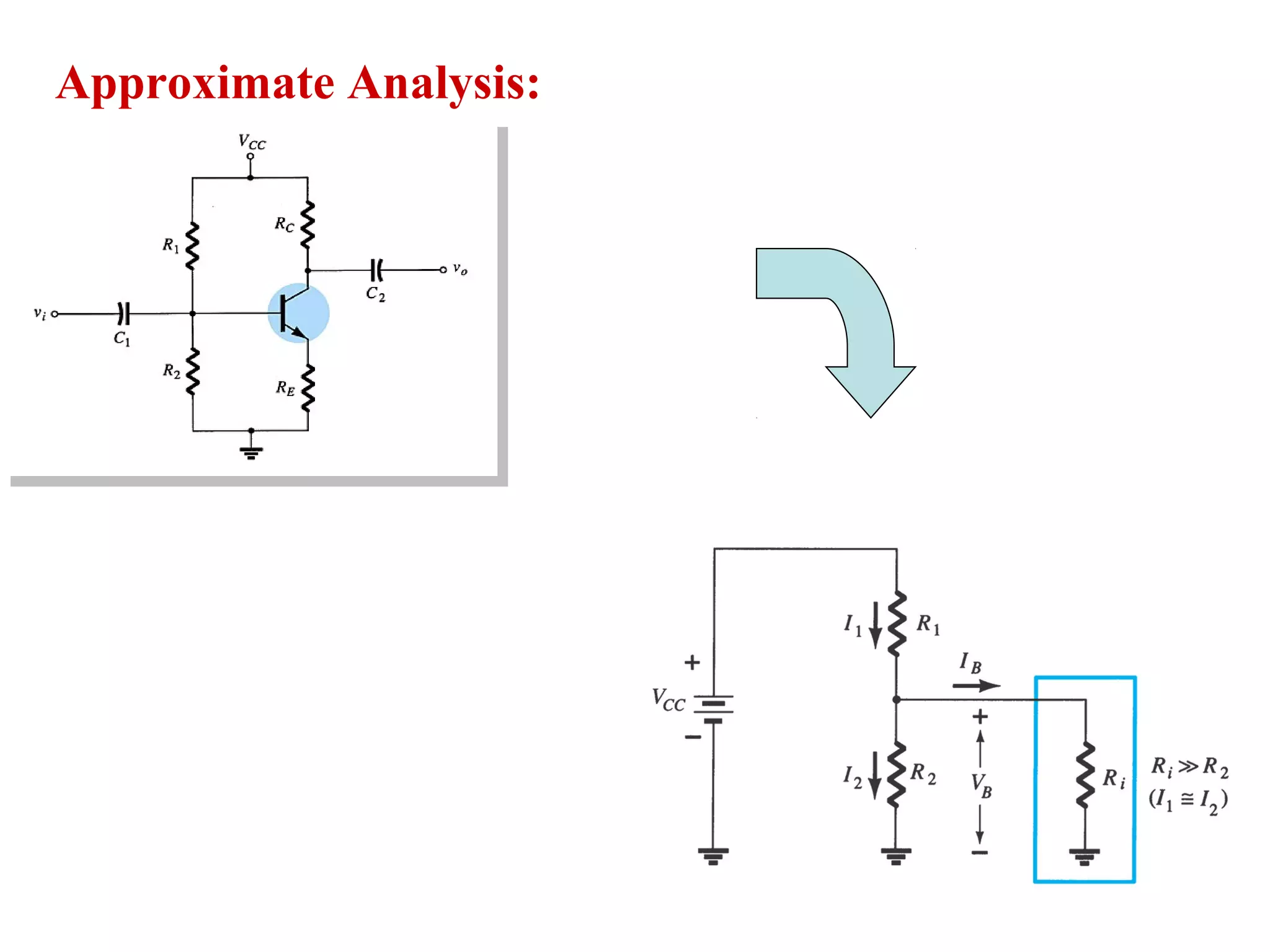
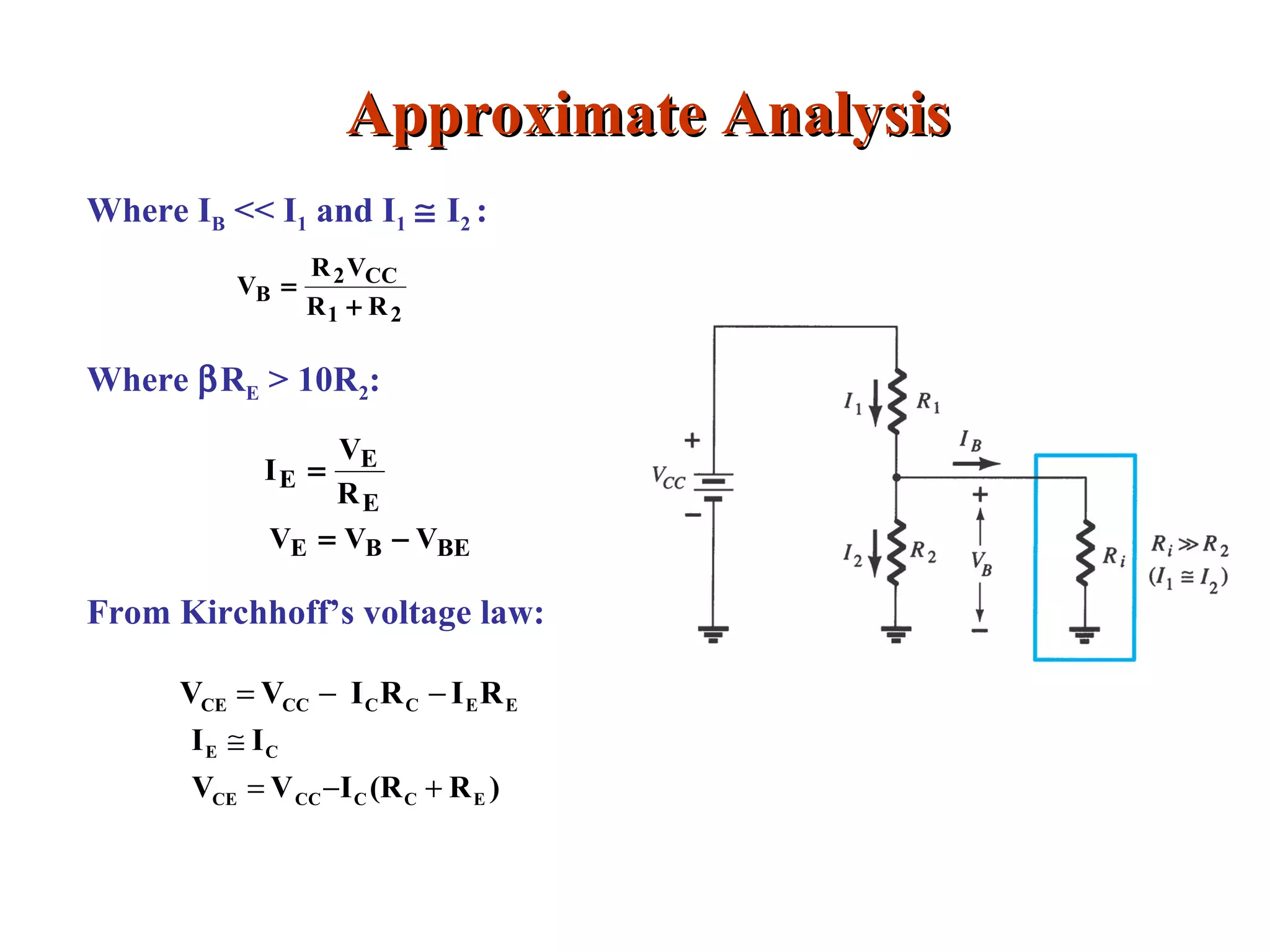
DC biasing applies fixed voltages to transistors to place them in an operating region for amplification. The operating point defines the transistor's quiescent operating conditions under DC. Stability refers to a circuit's insensitivity to parameter variations like temperature. Emitter-stabilized and voltage divider biasing improve stability over fixed biasing by incorporating an emitter or voltage divider resistor. Feedback biasing further increases stability by introducing negative feedback from collector to base.

1. DC Biasing of BJTs

2. BiasingBiasing
Biasing:Biasing: TThe DC voltages applied to
a transistor in order to turn it on so
that it can amplify the AC signal.

3. Operating PointOperating Point
The DC input
establishes an
operating or
quiescent point
called the Q-pointQ-point.

4. The Three States of OperationThe Three States of Operation
• Active or Linear Region OperationActive or Linear Region Operation
Base–Emitter junction is forward biased
Base–Collector junction is reverse biased
• Cutoff Region OperationCutoff Region Operation
Base–Emitter junction is reverse biased
• Saturation Region OperationSaturation Region Operation
Base–Emitter junction is forward biased
Base–Collector junction is forward biased

5. No matter what type of configuration a transistor
is used in, the basic relationships between the
currents are always the same, and the base-to-
emitter voltage is the threshold value if the
transistor is in the “on” state
BC
CBE
BE
II
III
VV
β
β
=
≅+=
=
)1(
7.0

6. • The operating point defines where the
transistor will operate on its characteristics
curves under dc conditions.
• For linear (minimum distortion)
amplification, the dc operating point should
not be too close to the maximum power,
voltage, or current rating and should avoid
the regions of saturation and cutoff

7. DC Biasing CircuitsDC Biasing Circuits
• Fixed-bias circuit
• Emitter-stabilized bias circuit
• Voltage divider bias circuit
• DC bias with voltage feedback

8. I. Fixed BiasI. Fixed Bias
• The fixed-bias configuration is the
simplest of transistor biasing
arrangements, but it is also quite unstable
•For most configurations the dc analysis
begins with a determination of the base
current
•For the dc analysis of a transistor
network, all capacitors are replaced by an
open-circuit equivalent

9. Fixed-bias circuit

10. The dc equivalent circuit of the fixed bias circuit
where the capacitor is replaced with an open-circuit

11. The Base-Emitter LoopThe Base-Emitter Loop
From Kirchhoff’s voltage
law:
+VCC – IBRB – VBE = 0
Solving for base current:
B
BECC
B
R
VV
I
−
=

12. Collector-Emitter LoopCollector-Emitter Loop
Collector current:
BII C
β=
CCCCCE RIVV −=
From Kirchhoff’s voltage law:
0=−+ CCCCCE VRIV

13. Example: Determine the following for the fixed-bias
configuration of the figure shown:
(a) IBQ and ICQ (b) VCEQ (c) VB and VC (d) VBC
β = 75

14. SaturationSaturation
• Saturation conditions are normally avoided because
the base-collector junction is no longer reverse-
biased and the output amplified signal will be
distorted
•For a transistor operating in the saturation region,
the current is a maximum value for the particular
design. Change the design and the corresponding
saturation level may rise or drop
•The highest saturation level is defined by the
maximum collector current as provided by the
specification sheet

15. SaturationSaturation

16. Ω=== 0
0
satCC
CE
CE
I
V
I
V
R
C
CC
C
R
V
I sat
=

17. SaturationSaturation
When the transistor is operating in saturation, current
through the transistor is at its maximum possible value.
CR
CCV
CsatI =
V0CEV ≅
In the previous example, the saturation level for the network is
given by:
mA
k
V
R
V
I
C
CC
Csat
45.5
2.2
12
=
Ω
==

18. Load Line AnalysisLoad Line Analysis
CCCCCE RIVV −=
The variables IC and VCE are related by the equation:

19. Load Line AnalysisLoad Line Analysis
IICsatCsat
ICC = VCCCC / RCC
VCECE = 0 V
VVCEcutoffCEcutoff
VCECE = VCCCC
ICC = 0 mA
The Q-point is the operating point:
• where the value of RB sets the value of IB
• that sets the values of VCE and IC
The end points of the load line are:

20. Circuit Values Affect the Q-PointCircuit Values Affect the Q-Point
[Movement of the Q-point with increasing level of IB]

21. Circuit Values Affect the Q-PointCircuit Values Affect the Q-Point
[Effect of an increasing level of RC on the load line the
Q-point]

22. Circuit Values Affect the Q-PointCircuit Values Affect the Q-Point
[Effect of lower values of VCC on the load line the Q-
point]

23. II. Emitter-Stabilized Bias CircuitII. Emitter-Stabilized Bias Circuit
Adding a resistor
(RE) to the emitter
circuit stabilizes
the bias circuit.

24. Base-Emitter LoopBase-Emitter Loop
From Kirchhoff’s voltage law:
0RI-V-RI- EEBEBBCC =+V
0R1)I(-V-RI-V EBBEBBCC =+β
Since IE = (β + 1)IB:
EB
BECC
B
1)R(R
V-V
I
+β+
=
Solving for IB:

25. Collector-Emitter LoopCollector-Emitter Loop
From Kirchhoff’s voltage law:
0
CC
V
C
R
C
I
CE
V
E
R
E
I =−++
Since IE ≅ IC:
)R(RI–VV ECCCCCE +=
Also:
EBEBRCCB
CCCCECEC
EEE
VVRI–VV
RI-VVVV
RIV
+==
=+=
=

26. Example: Determine the following for the emitter bias network
of the figure shown:
(a) IB (b) IC (c) VCE (d) VC (e) VE (f) VB (g) VBC
+16 V
β = 75

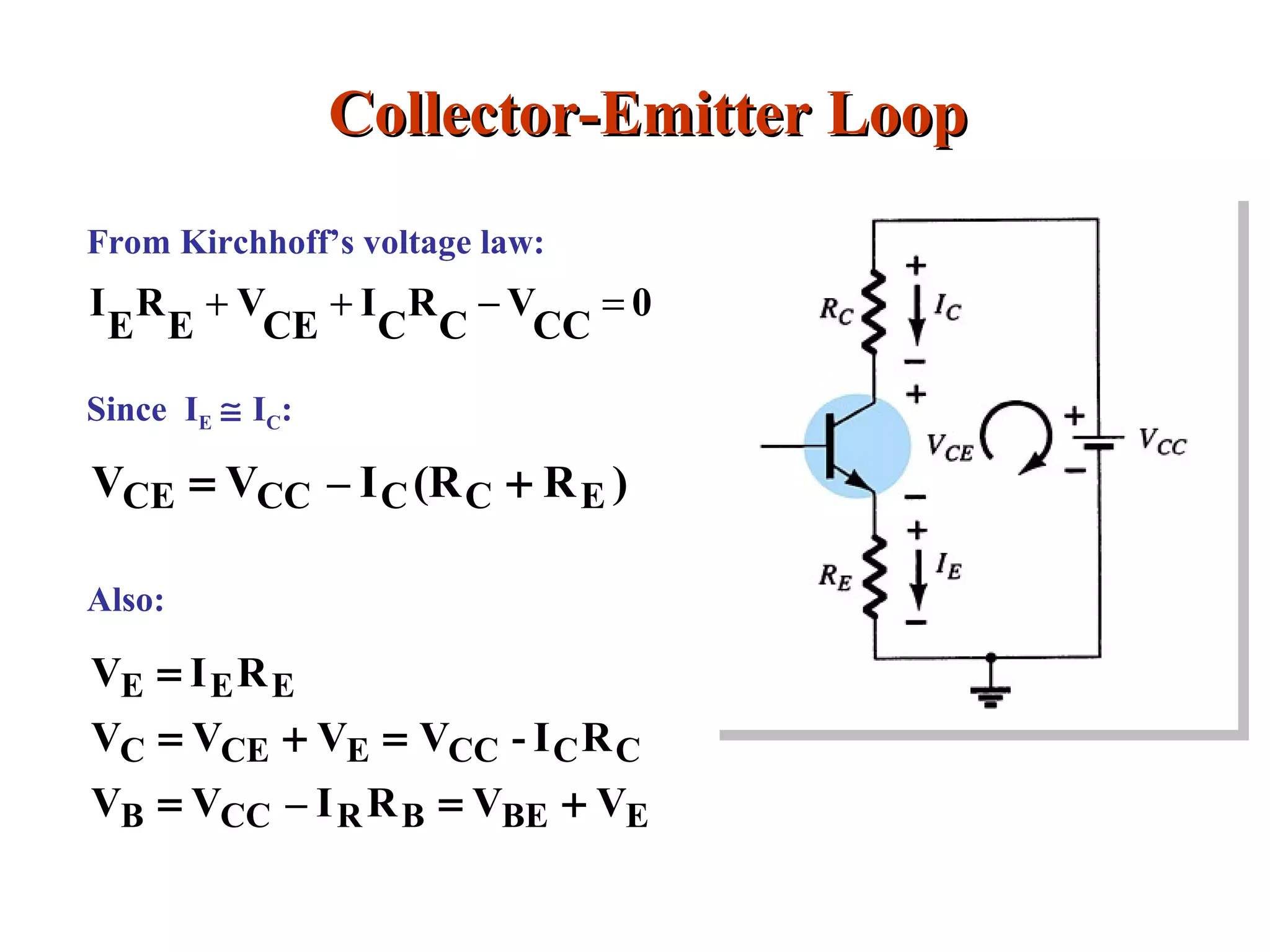
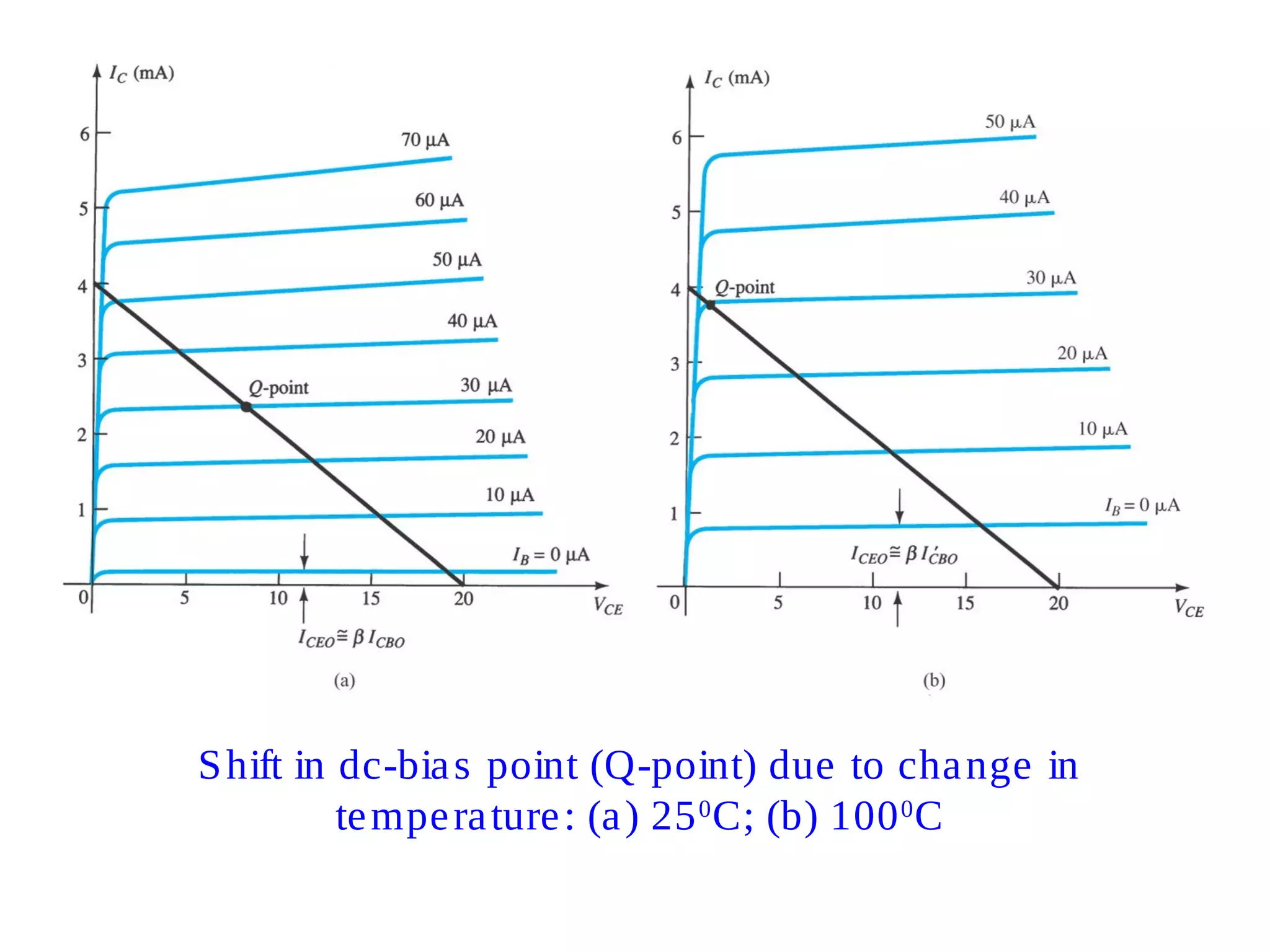
27. Improved Biased StabilityImproved Biased Stability
Stability refers to a circuit condition in which the currents
and voltages will remain fairly constant over a wide range
of temperatures and transistor Beta (β) values
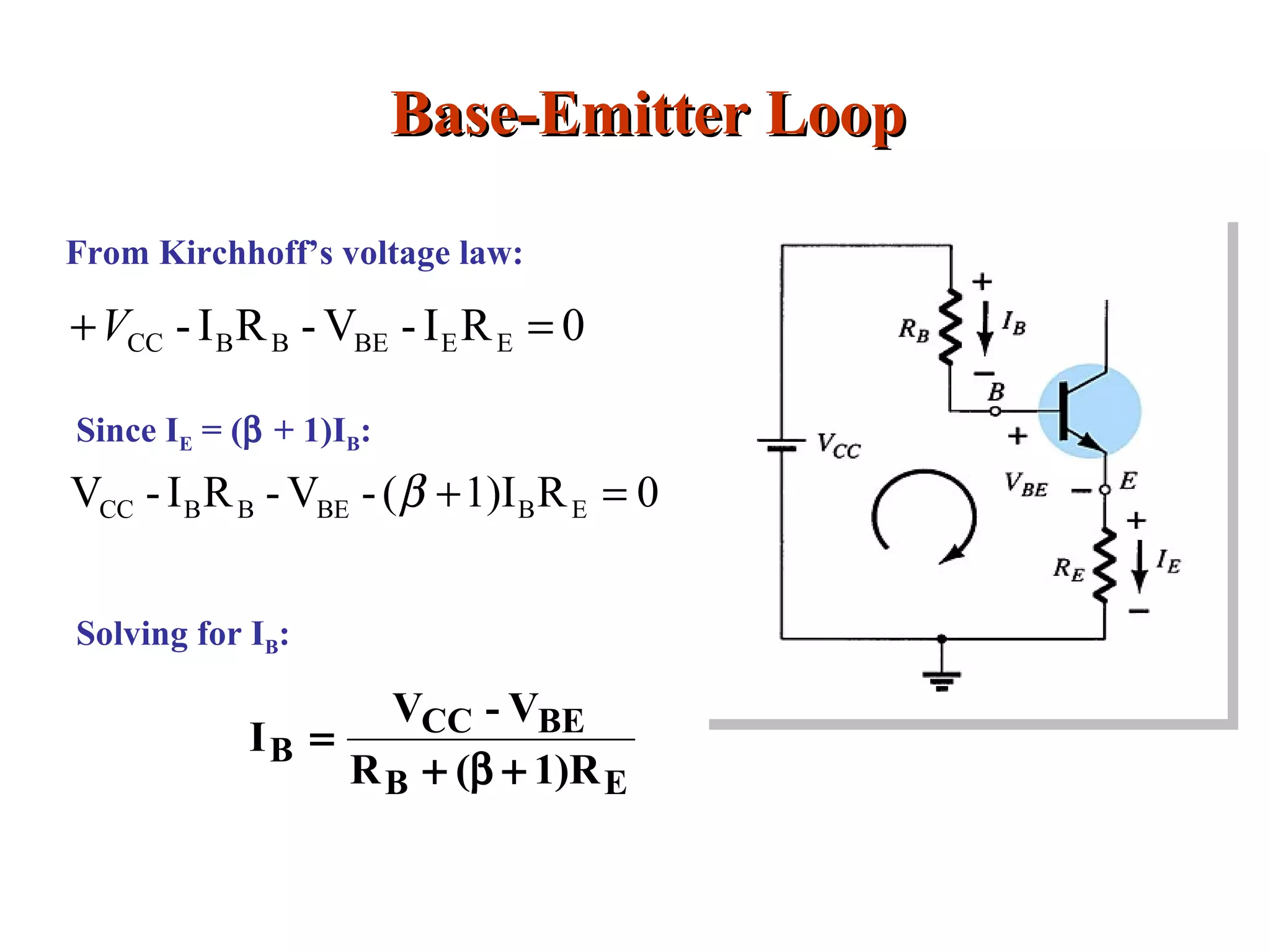
Adding RE to the emitter improves the stability of a transistor
β IB(µA) IC(mA) VCE(V)
75 30.24 2.27 9.91
100 28.81 3.63 9.11
[For Emitter Bias Case]
β IB(µA) IC(mA) VCE(V)
75 47.08 3.53 4.23
100 47.08 4.71 1.64
[For Fixed Bias Case]

28. Saturation LevelSaturation Level
EC
CC
C
RR
V
I sat
+
=

29. Load-line AnalysisLoad-line Analysis
VCEcutoff:: ICsat:
The endpoints can be determined from the load line.
mA0I
VV
C
CCCE
=
=
ERCR
CCV
CI
CE V0V
+
=
=
)( ECCCCCE RRIVV +−=

30. III. Voltage Divider BiasIII. Voltage Divider Bias
This is a very stable
bias circuit.
The currents and
voltages are nearly
independent of anyany
variations in β.

31. Exact Analysis:

33. 21 || RRRTh =
21
2
2
RR
VR
VE CC
RTh
+
==
)( ECCCCCE RRIVV +−=
0=−−− EEBEThBTh RIVRIE
Applying Kirchhoff’s voltage law in the clockwise direction in the
Thevenin network,
ETh
BETh
B
RR
VE
I
)1( ++
−
=
β
(Substituting IE = (β+1)IB)

34. Approximate Analysis:

35. Approximate AnalysisApproximate Analysis
Where IB << I1 and I1 ≅ I2 :
Where βRE > 10R2:
From Kirchhoff’s voltage law:
21
CC2
B
RR
VR
V
+
=
E
E
E
R
V
I =
BEBE VVV −=
EECCCCCE RIRIVV −−=
)R(RIVV
II
ECCCCCE
CE
+−=
≅

36. Voltage Divider Bias AnalysisVoltage Divider Bias Analysis
Transistor Saturation LevelTransistor Saturation Level
EC
CC
CmaxCsat
RR
V
II
+
==
Load Line AnalysisLoad Line Analysis
Cutoff:Cutoff: Saturation:Saturation:
mA0I
VV
C
CCCE
=
=
V0VCE
ERCR
CCV
CI
=
+
=

37. IV. DC Bias with Voltage FeedbackIV. DC Bias with Voltage Feedback
Another way to
improve the stability
of a bias circuit is to
add a feedback path
from collector to
base.
In this bias circuit
the Q-point is only
slightly dependent on
the transistor beta,
β.

38. Base-Emitter LoopBase-Emitter Loop
)R(RR
VV
I
ECB
BECC
B
+β+
−
=
From Kirchhoff’s voltage law:From Kirchhoff’s voltage law:
0RI–V–RI–RI–V EEBEBBCCCC =′
Where IWhere IBB << I<< ICC::
C
I
B
I
C
I
C
I' ≅+=
Knowing IKnowing ICC == ββIIBB and Iand IEE ≅≅ IICC, the loop, the loop
equation becomes:equation becomes:
0RIVRIRI–V EBBEBBCBCC =β−−−β
Solving for ISolving for IBB::

39. Collector-Emitter LoopCollector-Emitter Loop
Applying Kirchoff’s voltage law:Applying Kirchoff’s voltage law:
IERE + VCE + I’CRC – VCC = 0
Since ISince I′′CC ≅≅ IICC and Iand IEE ≅≅ IICC::
IC(RC + RE) + VCE – VCC =0
Solving for VSolving for VCECE::
VCE = VCC – IC(RC + RE)

40. Base-Emitter Bias AnalysisBase-Emitter Bias Analysis
Transistor Saturation LevelTransistor Saturation Level
EC
CC
CmaxCsat
RR
V
II
+
==
Load Line AnalysisLoad Line Analysis
Cutoff:Cutoff: Saturation:Saturation:
mA0I
VV
C
CCCE
=
=
V0VCE
E
R
C
R
CC
V
C
I
=
+
=

41. Bias StabilizationBias Stabilization
The stability of a system is a measure of the
sensitivity of a network to variations in its
parameters
In any amplifier employing a transistor the
collector current IC is sensitive to each of the
following parameters:
• β: increase with increase in temperature
• |VBE| : decrease about 2.5 mV per o
C
increase in temperature
• ICO (reverse saturation current): doubles in
value for every 100
increase in tempearture

42. Shift in dc-bias point (Q-point) due to change in
temperature: (a) 250
C; (b) 1000
C

43. A better bias circuit is one that will stabilize or
maintain the dc-bias initially set, so that the amplifier
can be used in a changing-temperature environment
Stability Factors: S(ICO), S(VBE), and S(β)
CO
C
CO
I
I
IS
∆
∆
=)(
BE
C
BE
V
I
VS
∆
∆
=)(
β
β
∆
∆
= CI
S )(
Networks that are quite stable and relatively insensitive
to temperature variations have low stability factors
The higher the stability factor, the more sensitive is the
network to variations in that parameter

44. S(ICO):
Emitter-Bias Configuration
)/()1(
)/(1
)1()(
EB
EB
CO
RR
RR
IS
++
+
+=
β
β
)1()( += βCOIS
1
)1(
1
)1()( =→
+
+=
β
βCOIS
E
B
CO
R
R
IS ≅)(
For RB/RE >> (β+1),
For RB/RE << 1,
For the range where
RB/RE ranges between
1 and (β+1),

45. [Variation of stability factor with the resistor ratio RB/RE for
the emitter-bias configuration]

46. )1()( += βCOIS
)/()1(
)/(1
)1()(
ETh
ETh
CO
RR
RR
IS
++
+
+=
β
β
)/()1(
)/(1
)1()(
CB
CB
CO
RR
RR
IS
++
+
+=
β
β
Fixed-Bias Configuration:
Voltage-Divider Bias Configuration:
Feedback-Bias Configuration:

47. S(VBE):
EB
BE
RR
VS
)1(
)(
++
−
=
β
β
Emitter-bias configuration:
Fixed-Bias Configuration:
B
BE
R
VS
β−
=)(
EB
BE
RR
VS
)1(
)(
++
−
=
β
β
)1(/
/
)(
++
−
=⇒
β
β
EB
E
BE
RR
R
VS
E
EE
BE
R
RR
VS
1/
)1(
/
)( −=
−
≅
+
−
≅⇒
β
β
β
β For (β+1)>>RB/RE
This shows that the larger the resistance RE, the lower is
the stability factor and the more stable is the system

48. S(β):
Emitter-bias configuration:
)/1(
)/1(
)(
21
1
EB
EBCC
RR
RRII
S
++
+
=
∆
∆
=
βββ
β
1
1
)(
β
β CI
S =
)/1(
)/1(
)(
21
1
ETh
EThC
RR
RRI
S
++
+
=
ββ
β
Fixed-Bias Configuration:
Voltage-Divider Bias Configuration:
Feedback-Bias Configuration:
))1((
)(
)(
21
1
ββ
β
++
+
=
CB
CBC
RR
RRI
S

49. Summary
The total effect on the collector current can be determined using
the following equation:
ββ ∆+∆+∆=∆ )()()( SVVSIISI BEBECOCOC