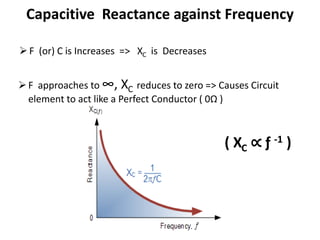
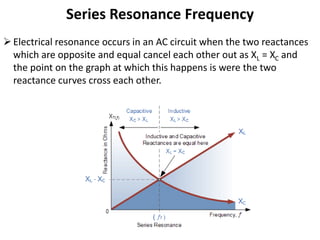
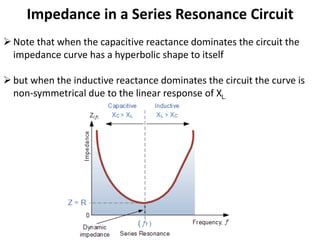
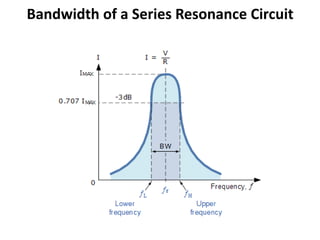
This unit covers series and parallel resonance, quality factor, bandwidth, self and mutual inductance, and coefficient of coupling. It discusses resonance occurring when the applied voltage and source current are in phase, making the circuit purely resistive. At resonance, the power factor is unity. Series resonance occurs when the inductive and capacitive reactances are equal in magnitude but cancel each other out. This happens at the resonant frequency. Applications of series resonance circuits include AC mains filters and radio/TV tuning circuits. The bandwidth, selectivity, and quality factor of series resonance circuits are also defined in relation to the resonant frequency, current, and cutoff frequencies.