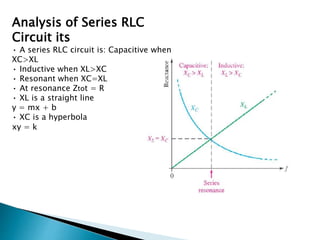
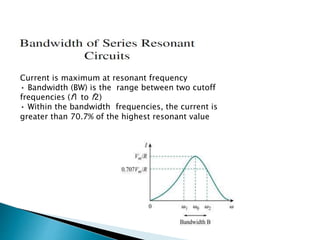
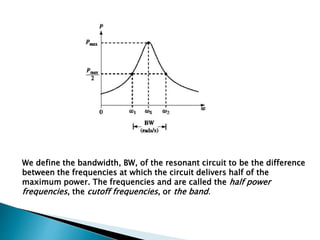
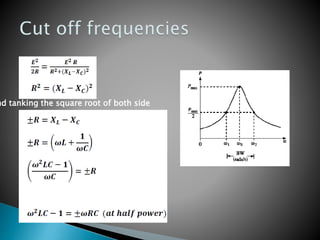
The document discusses series and parallel resonance circuits. Some key points: - In a series RLC circuit, the impedance is purely resistive at resonance when the inductive and capacitive reactances are equal. Maximum current flows at this resonant frequency. - Parallel RLC circuits also exhibit resonance when the reactances cancel out. Minimum current flows at resonance for a parallel circuit. - For both circuits, the quality factor Q and bandwidth depend on the resistance, with lower resistance leading to higher Q and narrower bandwidth.

1. Series and parallel Resonance
Dr/Ghada Kareem

2. Therefore at the resonant frequency the impedance seen by
the source is purely resistive.
• This implies that at resonance the inductor/capacitor
combination acts as a short circuit.
• The current flowing in the system is in phase with the
source voltage.

3. Analysis of Series RLC
Circuit its
• A series RLC circuit is: Capacitive when
XC>XL
• Inductive when XL>XC
• Resonant when XC=XL
• At resonance Ztot = R
• XL is a straight line
y = mx + b
• XC is a hyperbola
xy = k

4. Series RLC impedance as a function of frequency.
Graph Including Ztot = R at Resonance

5. Series Resonance
Resonance is a condition in a series RLC circuit in which the capacitive
and inductive
Reactances are equal in magnitude
• The result is a purely resistive impedance
• The formula for series resonance is:

6. Current is maximum at resonant frequency
• Bandwidth (BW) is the range between two cutoff
frequencies (f1 to f2)
• Within the bandwidth frequencies, the current is
greater than 70.7% of the highest resonant value

7. The quality factor increases with decreasing R
• The bandwidth decreases with decreasing R

8. The 70.7% cutoff point is also referred to as:
•The Half Power Point
•-3dB Point

9. Due to the changing impedance of the circuit, we conclude that
if a constant amplitude voltage is applied to the series resonant
circuit, the current and power of the circuit will not be constant
at all frequencies. In this section, we examine how current and
power are affected by changing the frequency of the voltage
source.
Applying Ohm’s law gives the magnitude of the current as
follows:

10. When the frequency is zero (D.C), the current will be zero since
the capacitor is effectively an open circuit.
On the other hand, at increasingly higher frequencies, the
inductor begins to approximate an open circuit, once again
causing the current in the circuit to approach zero.
The total power dissipated by the circuit at any frequency is
given as
Since the current is maximum at resonance, it follows that the power
must similarly be maximum at resonance. The maximum power
dissipated by the series resonant circuit is therefore given as

11. Half-power frequencies
are those frequencies at which the power delivered is one-
half that delivered at the resonant frequency
The power response of a series resonant circuit has a bell-shaped curve
called the selectivity curve, which is similar to the current response.

12. We define the bandwidth, BW, of the resonant circuit to be the difference
between the frequencies at which the circuit delivers half of the
maximum power. The frequencies and are called the half power
frequencies, the cutoff frequencies, or the band.

13. If the bandwidth of a circuit is kept very narrow, the circuit
is said to have a high selectivity. On the other hand, if the
bandwidth of a circuit is large, the circuit is said to have a
low selectivity.
The elements of a series resonant circuit determine not
only the frequency at which the circuit is resonant, but also
the shape (and hence the bandwidth) of the power
response curve.
Consider a circuit in which the resistance, R, and the
resonant frequency, are held constant

14. For the series resonant circuit the power at any
frequency is determined as
At the half-power frequencies, the power must be
The cutoff frequencies are found by evaluating the
frequencies at which the power dissipated by the
circuit is half of the maximum power

15. nd tanking the square root of both side

16. .

18. Parallel Resonance Circuit
It is usually called tank circuit
Ideal Circuits Practical Circuits
Complex Configuration

19. Ideal Parallel Resonance Circuit
The total admittance

20. Ideal Parallel Resonance Circuit
At parallel resonance:
At resonance, the admittance consists only conductance G =
1/R.
The value of current will be minimum since the total admittance
is minimum.
The voltage and current are in phase (Power factor is unity).
The inductor and capacitor reactances cancel, resulting in a
circuit voltage
simply determined by Ohm’s law as:
The frequency response of the impedance of the parallel circuit
is shown
exactly
opposite
to
that in
series
resonant
circuits

21. Ideal Parallel Resonance Circuit
Parallel resonant circuit has same parameters as the series
resonant circuit.
Resonance frequency:
Half-power frequencies:
Bandwidth and Q-factor:

23. Summary of the properties of RLC resonant circuits.

25. Example: In the parallel RLC circuit, let R=8 kΩ, L=0.2 mH and
C=8 μF.
(a)Calculate 𝜔o, Q, and B.
(b)Calculate 𝜔1 and 𝜔2.
(c)Determine the power dissipated at 𝜔o.

28. A parallel resonance circuit has a resistance of 2 kΩ and half-power frequencies of
86 kHz and 90 kHz. Determine:
(a) the capacitance (b) the inductance
(c) the resonant frequency (d) the bandwidth
(e) the quality factor

30. Assignment :
For the circuit:
(a) Calculate the resonant frequency ωo, the quality factor Q,
and the bandwidth B.
(b) What value of capacitance must be connected in series
with the 20 μF capacitor in order to double the bandwidth?.

31. 1-The total current into the L and C branches of a
parallel circuit at resonance is ideally
(a) maximum (b) low (c) high (d) zero
2-The resonant frequency of a parallel circuit is
approximately the same as a series circuit when
(a) the Q is very low (b) the Q is very high
(c) there is no resistance (d) either answer (b) or (c)
3-If the resistance in parallel with a parallel resonant circuit
is reduced, the bandwidth
(a) disappears (b) decreases
c) becomes sharper d) increases