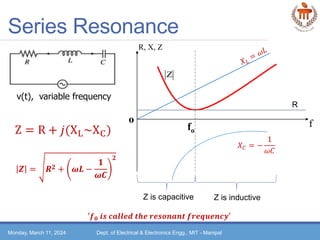
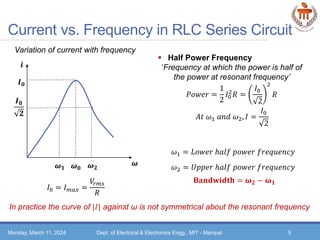
This document discusses resonance in series and parallel RLC circuits. It defines resonant frequency as when the inductive and capacitive reactances are equal in a series circuit. The half power frequencies and quality factor are also defined. Expressions for calculating the resonant frequency, half power frequencies, and quality factor of series RLC circuits are provided. Resonance in parallel RLC circuits is also covered, including the process for obtaining the resonant frequency expression. Worked examples demonstrate applying the concepts.

1. Basic Electrical Technology
[ELE 1051]
SINGLE PHASE AC CIRCUITS
L20 -Resonance
Monday, March 11, 2024 Dept. of Electrical & Electronics Engg., MIT - Manipal 1

2. Topics covered…
 Resonance in series RLC circuit
 What is half power frequency, bandwidth and quality factor in
series RLC circuit?
 Resonance in parallel circuits
Monday, March 11, 2024 Dept. of Electrical & Electronics Engg., MIT - Manipal 2

3. Series Resonance
Monday, March 11, 2024 Dept. of Electrical & Electronics Engg., MIT - Manipal
v(t), variable frequency
Z = R + 𝑗(XL~XC)
f
o
Z
R
fo
𝑋𝐶 = −
1
𝜔𝐶
𝒁 = 𝑹𝟐 + 𝝎𝑳 −
𝟏
𝝎𝑪
𝟐
R, X, Z
′𝒇𝟎 𝒊𝒔 𝒄𝒂𝒍𝒍𝒆𝒅 𝒕𝒉𝒆 𝒓𝒆𝒔𝒐𝒏𝒂𝒏𝒕 𝒇𝒓𝒆𝒒𝒖𝒆𝒏𝒄𝒚′
Z is inductive
Z is capacitive

4. Series Resonance
 When series RLC circuit is at resonance,
o Current is in phase with voltage
o Circuit power factor is unity
o 𝑋𝐿 = 𝑋𝐶
o 𝑍 = 𝑅
 Resonant frequency for a series RLC circuit is obtained as follows:
Monday, March 11, 2024 Dept. of Electrical & Electronics Engg., MIT - Manipal 4
𝑋𝐿 = 𝑋𝐶
𝜔0𝐿 =
1
𝜔0𝐶
𝒇𝟎 =
𝟏
𝟐𝝅 𝑳𝑪
𝒉𝒆𝒓𝒕𝒛
Imaginary p𝑎𝑟𝑡 𝑜𝑓 𝑍𝑒𝑞 = 0
v(t), variable frequency
Z = R + 𝑗(XL~XC)

5. Current vs. Frequency in RLC Series Circuit
Monday, March 11, 2024 Dept. of Electrical & Electronics Engg., MIT - Manipal 5
Variation of current with frequency
𝐼0 = 𝐼𝑚𝑎𝑥 =
𝑉
𝑟𝑚𝑠
𝑅
𝑰𝟎
𝒊
𝑰𝟎
𝟐
𝝎
𝝎𝟎
𝝎𝟏 𝝎𝟐
 Half Power Frequency
‘Frequency at which the power is half of
the power at resonant frequency’
𝑃𝑜𝑤𝑒𝑟 =
1
2
𝐼0
2
𝑅 =
𝐼0
2
2
𝑅
𝜔1 = 𝐿𝑜𝑤𝑒𝑟 ℎ𝑎𝑙𝑓 𝑝𝑜𝑤𝑒𝑟 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦
𝜔2 = 𝑈𝑝𝑝𝑒𝑟 ℎ𝑎𝑙𝑓 𝑝𝑜𝑤𝑒𝑟 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦
𝐴𝑡 𝜔1 𝑎𝑛𝑑 𝜔2, 𝐼 =
𝐼0
2
𝐁𝐚𝐧𝐝𝐰𝐢𝐝𝐭𝐡 = 𝛚𝟐 − 𝛚𝟏
In practice the curve of |𝐼| against ω is not symmetrical about the resonant frequency

6. Half Power Frequency
Monday, March 11, 2024 Dept. of Electrical & Electronics Engg., MIT - Manipal 6
𝐼𝑚𝑝𝑒𝑑𝑎𝑛𝑐𝑒 𝑎𝑡 𝜔1𝑎𝑛𝑑 𝜔2, |𝑍| =
𝑉0
𝐼0
2
= 2𝑅
Below Resonant frequency 𝜔0, 𝑋𝐶 > |𝑋𝐿| Above Resonant frequency 𝜔0, 𝑋𝐿 > |𝑋𝐶|
At 𝜔1,
𝑅2 + 𝑋𝐶 − 𝑋𝐿
2 = 2𝑅
𝑋𝐶 − 𝑋𝐿 = 𝑅
1
𝜔1𝐶
− 𝜔1𝐿 = R
𝝎𝟏 =
−𝑹
𝟐𝑳
+
𝑹
𝟐𝑳
𝟐
+
𝟏
𝑳𝑪
At 𝜔2,
𝑅2 + 𝑋𝐿 − 𝑋𝐶
2 = 2𝑅
𝑋𝐿 − 𝑋𝐶 = 𝑅
𝜔2𝐿 −
1
𝜔2𝐶
= R
𝝎𝟐 =
𝑹
𝟐𝑳
+
𝑹
𝟐𝑳
𝟐
+
𝟏
𝑳𝑪
𝝎𝟐 − 𝝎𝟐 =
𝑹
𝑳
𝝎𝟐𝝎𝟏 =
𝟏
𝑳𝑪
= 𝝎𝟎
𝟐

7. Quality Factor for series circuit
 At resonance, 𝑉𝐶 and 𝑉𝐿 can be very much greater than applied voltage
 High value of Q can lead to component damage
 Careful design necessary
 Larger the value of Q, more symmetrical the curve appears about the
resonant frequency
Monday, March 11, 2024 Dept. of Electrical & Electronics Engg., MIT - Manipal 7
𝑉𝐶 = 𝐼 𝑋𝐶 =
𝑉. 𝑋𝐶
𝑅2 + 𝑋𝐿 − 𝑋𝐶
2
At resonance, 𝑋𝐿 = 𝑋𝐶
𝑉𝐶 =
𝑉
𝑅
𝑋𝐶
𝑉𝐶 =
𝑉
𝜔0𝐶𝑅
= 𝑸𝑉
Q is termed the Q factor or voltage magnification
𝑸 =
𝟏
𝝎𝟎𝑪𝑹
=
𝝎𝟎𝑳
𝑹
=
𝟏
𝑹
𝑳
𝑪
𝑸 =
𝑹𝒆𝒔𝒐𝒏𝒂𝒏𝒕 𝒇𝒓𝒆𝒒𝒖𝒆𝒏𝒄𝒚
𝑩𝒂𝒏𝒅𝒘𝒊𝒅𝒕𝒉

8. Illustration 1
A circuit having a resistance of 4Ω and inductance of 0.5H and a
variable capacitance in series, is connected across a 100V,
50Hz supply. Calculate:
a) The capacitance to give resonance
b) The voltages across the inductor and the capacitor
c) The Q factor of the circuit
Monday, March 11, 2024 Dept. of Electrical & Electronics Engg., MIT - Manipal 8
Ans:
C = 20.3𝜇F
𝑉𝐶 = 𝑉𝐿 = 3930𝑉
Q = 39.3

9. Illustration 2
The bandwidth of a series resonant circuit is 500 Hz. If the
resonant frequency is 6000 Hz, what is the value of Q? If R =10
Ω, what is the value of the inductive reactance at resonance?
Calculate the inductance and capacitance of the circuit
Monday, March 11, 2024 Dept. of Electrical & Electronics Engg., MIT - Manipal 9
Ans:
Q = 12
𝑋𝐿 = 120Ω
L = 3.18mH; C = 0.22𝜇F

10. Resonance in parallel circuits
Steps to obtain the expression of resonant frequency in parallel circuits
o Obtain the net admittance of the circuit
o Equate the imaginary part (susceptance) to zero and obtain the expression of
𝜔𝑟
The expression for resonant frequency depends on circuit configuration
Monday, March 11, 2024 Dept. of Electrical & Electronics Engg., MIT - Manipal 10

11. Current vs. Frequency in parallel Circuits
 At resonance
o Impedance is maximum
o Resultant current minimum
Monday, March 11, 2024 Dept. of Electrical & Electronics Engg., MIT - Manipal 11
ωr
o
𝑰
𝝎

12. Illustration 1
Obtain the expression for resonant frequency for the given
parallel circuit
Monday, March 11, 2024 Dept. of Electrical & Electronics Engg., MIT - Manipal 12
𝒇𝒓 =
𝟏
𝟐𝝅
𝟏
𝑳𝑪
−
𝑹
𝑳
𝟐

13. Illustration 2
Show that circuit given in figure will be at resonance at supply
frequency
Monday, March 11, 2024 Dept. of Electrical & Electronics Engg., MIT - Manipal 13
vs=Cos(1.4t)
L=0.5H C=1F
5
Z = 0.099 at 𝜔 = 1.4 𝑟𝑎𝑑/𝑠𝑒𝑐