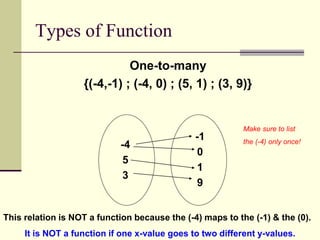
This document discusses relations and functions. It provides examples of how to classify relations as functions or not based on whether they satisfy the vertical line test and one-to-one correspondence. Students are asked to complete activities identifying domains and ranges of relations, graphing relations to apply the vertical line test, and determining if equations represent functions. The assignment is to copy equations on a sheet of paper and identify if they represent functions.

1. Relations
and
Functions

2. Classify Me!
Each group will pick a piece of paper and each paper
has a name of an object written on it (5 paper each
group). You will group the following objects in such a
way that they have common property/characteristics
then write on the right corner of the board the object
and its group in the form (object, common name). For
example, (pen, school supplies).
I will give marker to the two groups and during the
activity, the first member will do the task then s/he will
give the chalk to the next member. The group who will
finish first the activity will be the winner.

3. Objectives
• Illustrates a relation and a
function;
• Verify if a given relation is a
function.

4. “Representing a Relation”
In this activity, you will describe the mapping
diagram by writing the set of ordered pairs. The
first two coordinates are done for you.

5. What is a Relation?
A relation is a set of ordered pairs.
When you group two or more points in a set, it is
referred to as a relation. When you want to show that a
set of points is a relation you list the points in braces.
For example, if I want to show that the points (-3,1) ;
(0, 2) ; (3, 3) ; & (6, 4) are a relation, it would be written
like this:
{(-3,1) ; (0, 2) ; (3, 3) ; (6, 4)}

6. Domain and Range
 Each ordered pair has two parts, an x-value
and a y-value.
 The x-values of a given relation are called the
Domain.
 The y-values of the relation are called the
Range.
 When you list the domain and range of a
relation, you place each (the domain and the
range) in a separate set of braces.

7. For Example,
1. List the domain and the range of the relation
{(-3,1) ; (0, 2) ; (3, 3) ; (6, 4)}
Domain: { -3, 0, 3, 6} Range: {1, 2, 3, 4}
2. List the domain and the range of the relation
{(-3,3) ; (0, 2) ; (3, 3) ; (6, 4) ; ( 7, 7)}
Domain: {-3, 0, 3, 6, 7} Range: {3, 2, 4, 7}
Notice! Even though the number 3 is listed twice in the
relation, you only note the number once when you list the
domain or range!

8. Aside from ordered pairs, a relation may be
represented in four ways:
Table
x -2 -1 0 1 2
y -4 -2 0 2 4
Mapping
-2
-1
0
1
2
-4
-2
0
2
4

9. Aside from ordered pairs, a relation may be
represented in four ways:
Graph Rule or Equation
Notice that the
value of y is twice
the value of x. In
other words, this
can be described by
the equation y = 2x,
where x is an
integer from -2 to 2.

10. What is a Function?
Function is the relation in which each element of the
domain corresponds to exactly one element of the
range.
A function is a relation that assigns each
y-value only one x-value.
What does that mean? It means, in order for the
relation to be considered a function, there cannot be
any repeated values in the domain.
Note: every function is a relation, but not all relations are
function.

11. Types of Function
One-to-one
{(-3,1) ; (0, 2) ; (3, 3) ; (6, 4)}
-3
0
3
6
1
2
3
4
This relation is a function because each x-value maps to only one y-value.

12. Types of Function
Many-to-one
{(-1,2) ; (1, 2) ; (5, 3) ; (6, 8)}
-1
1
5
6
2
3
8
Notice that even
though there are
two 2’s in the
range, you only
list the 2 once.
This relation is a function because each x-value maps to only one y-value.
It is still a function if two x-values go to the same y-value.

13. Types of Function
One-to-many
{(-4,-1) ; (-4, 0) ; (5, 1) ; (3, 9)}
-4
5
3
-1
0
1
9
This relation is NOT a function because the (-4) maps to the (-1) & the (0).
It is NOT a function if one x-value goes to two different y-values.
Make sure to list
the (-4) only once!

14. Activity 2
Which of given tables express a function.
1.
X 1 1 1 1 1 1
y 2 3 4 5 6 7
2.
X 2 3 4 5 6 7
y 1 1 1 1 1 1
3.
x 10 20 30 40 50 60
y 24 46 27 18 17 38

15. Function rule/equation
The equation that represents a function is called a
function rule.
 A function rule is written with two variables, x
and y.
 It can also be written in function notation using f(x),
where f(x) represent the y value.
 F(x) is read as ‘y as a function of x’

16. Function rule/equation
The equation that represents a function is called a
function rule.
 A function is a rule, expressed as a formula/equation,
such that any allowable value of one variable
(independent variable) corresponds to a unique value
of a second variable (dependent variable).
 You have seen that not every set of ordered pair
defines a function. Similarly, not all equations with the
variables x and y define a function. If an equation is
solved for y and more than one value of y can be
obtained for a particular value of x, then the equation
does not defined y as a function of x.

17. Example:

18. Example:

19. Activity 3
Which of given rule/equation a function.

20. Function Graph
 Every graph illustrate a set of ordered
pairs. But not every graph in the x-y plane
represent function. The vertical line test is
the simplest way of determining whether or
not a graph represent a function.
 Vertical line test means a graph represents
a function if and only if no vertical line
intersect the graph at more than one point.

21. Examples of the Vertical Line Test
function
function
Not a function
Not a function
……….

22. Example:

23. Practice
Complete the following questions and check your answers on the
next slide.
1. Identify the domain and range of the following relations:
1. {(-4,-1) ; (-2, 2) ; (3, 1) ; (4, 2)}
2. Graph the following relations and use the vertical line test to see
if the relation is a function. Connect the pairs in the order given.
3. {(0,6) ; (3, 3) ; (0, 0)}
Determine wether each equation expressed y as a function of x
2. y = 3x + 7

24. Quiz
Get one whole sheet of paper and answer the following. This will
serve as your quiz.
Test 1!

25. Assignment:
For your assignment, copy these equations and write your answer in a
one whole sheet of paper.
Determine whether each rule below represents a function or not.