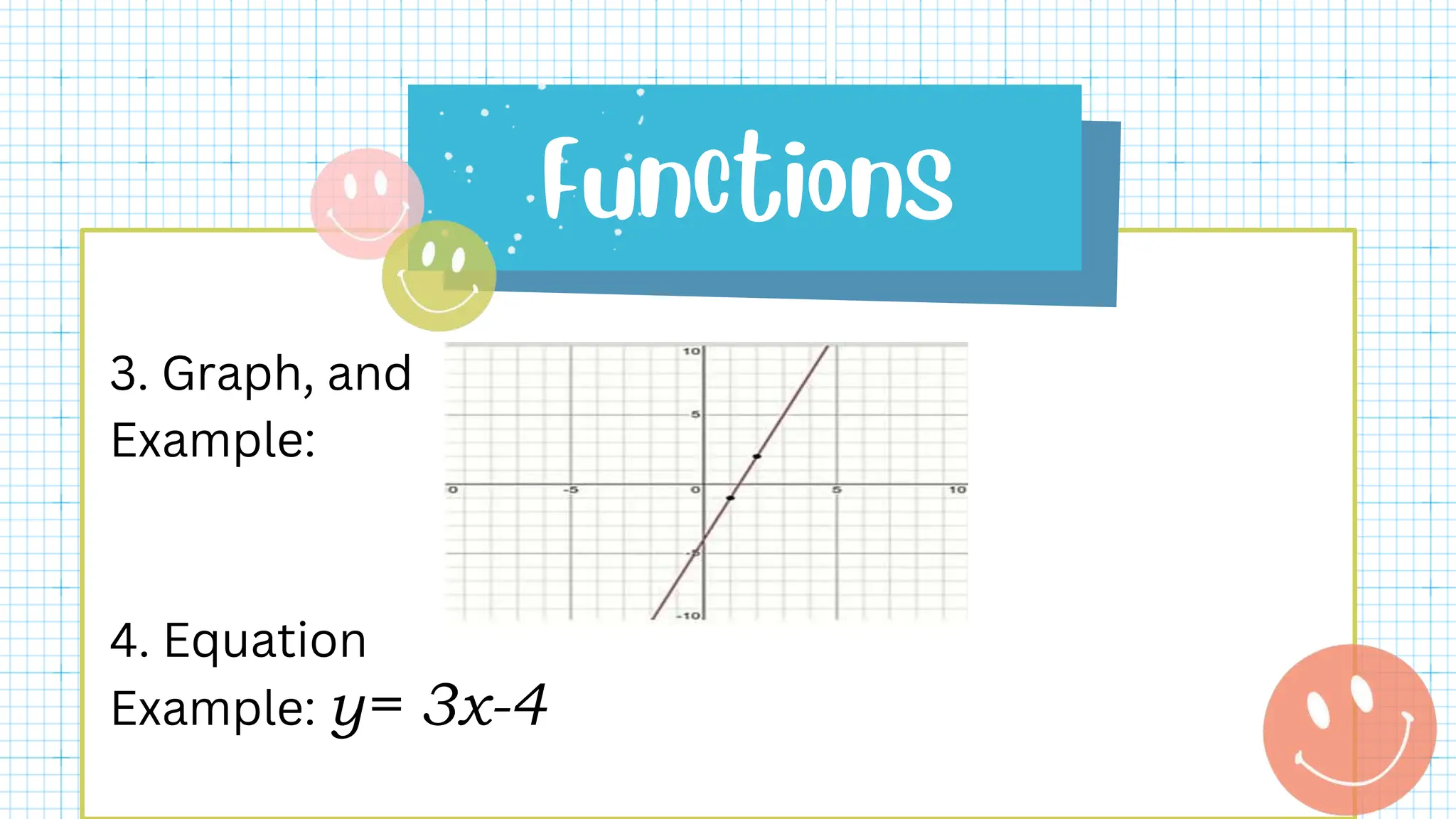
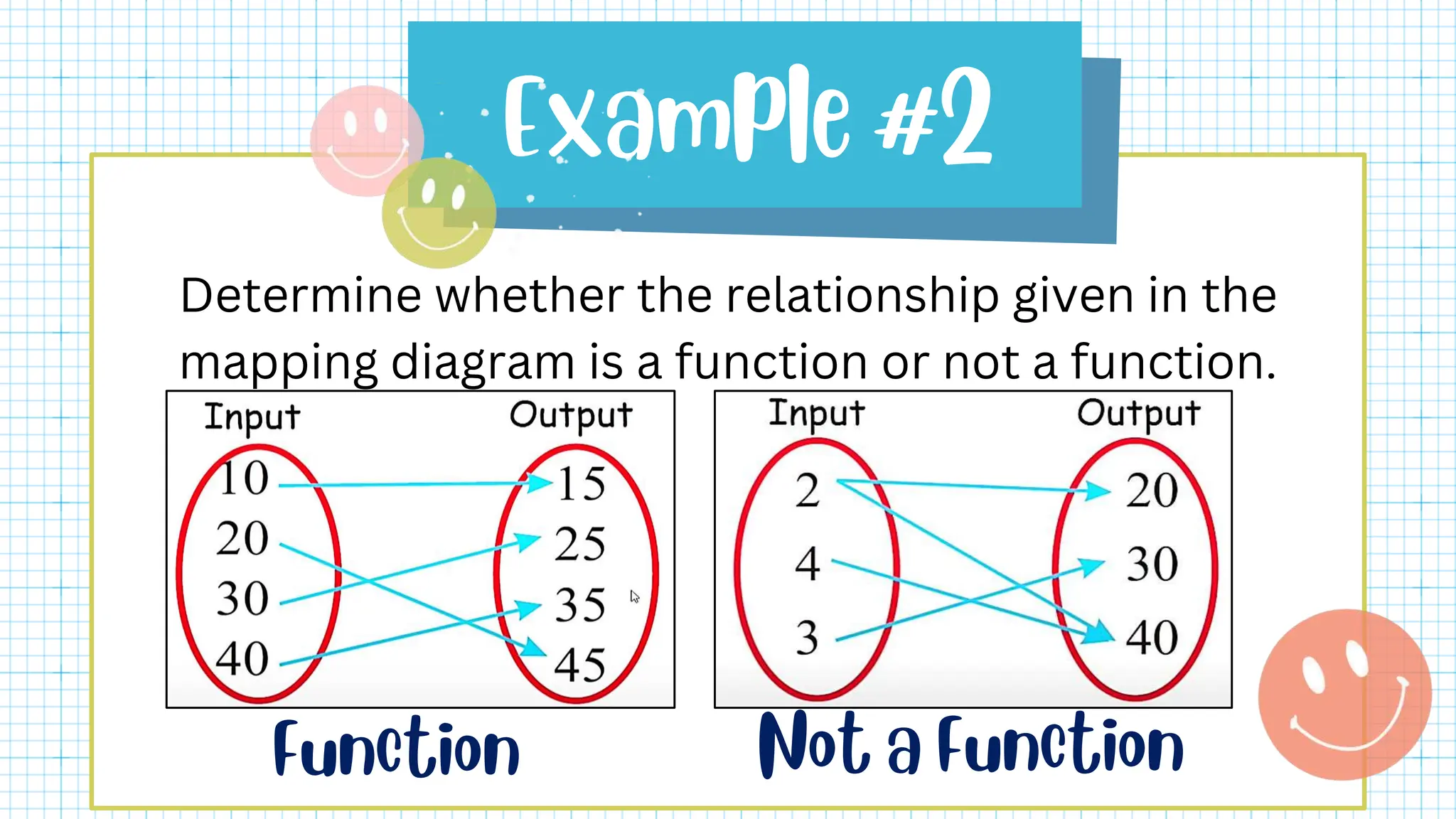
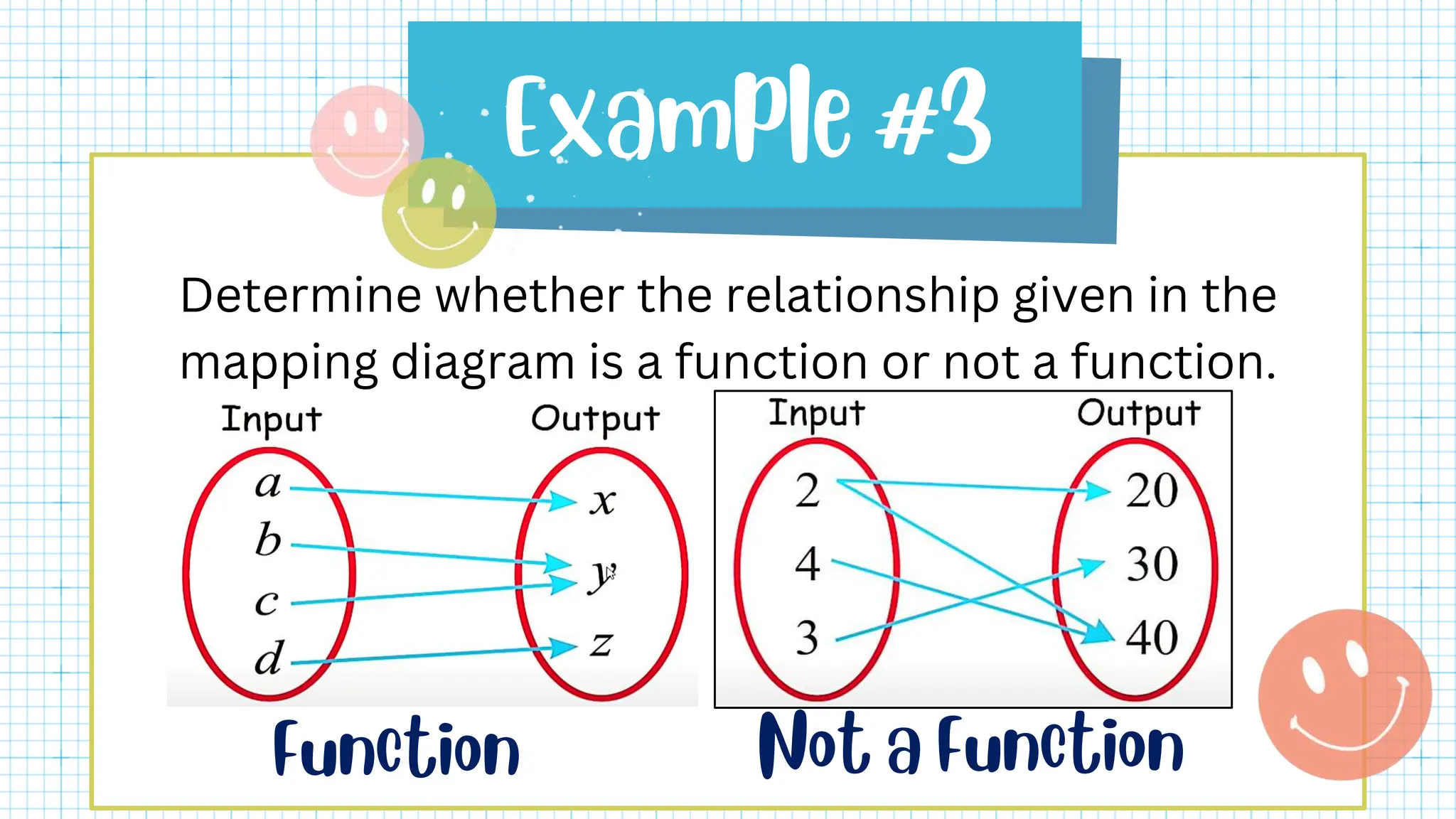
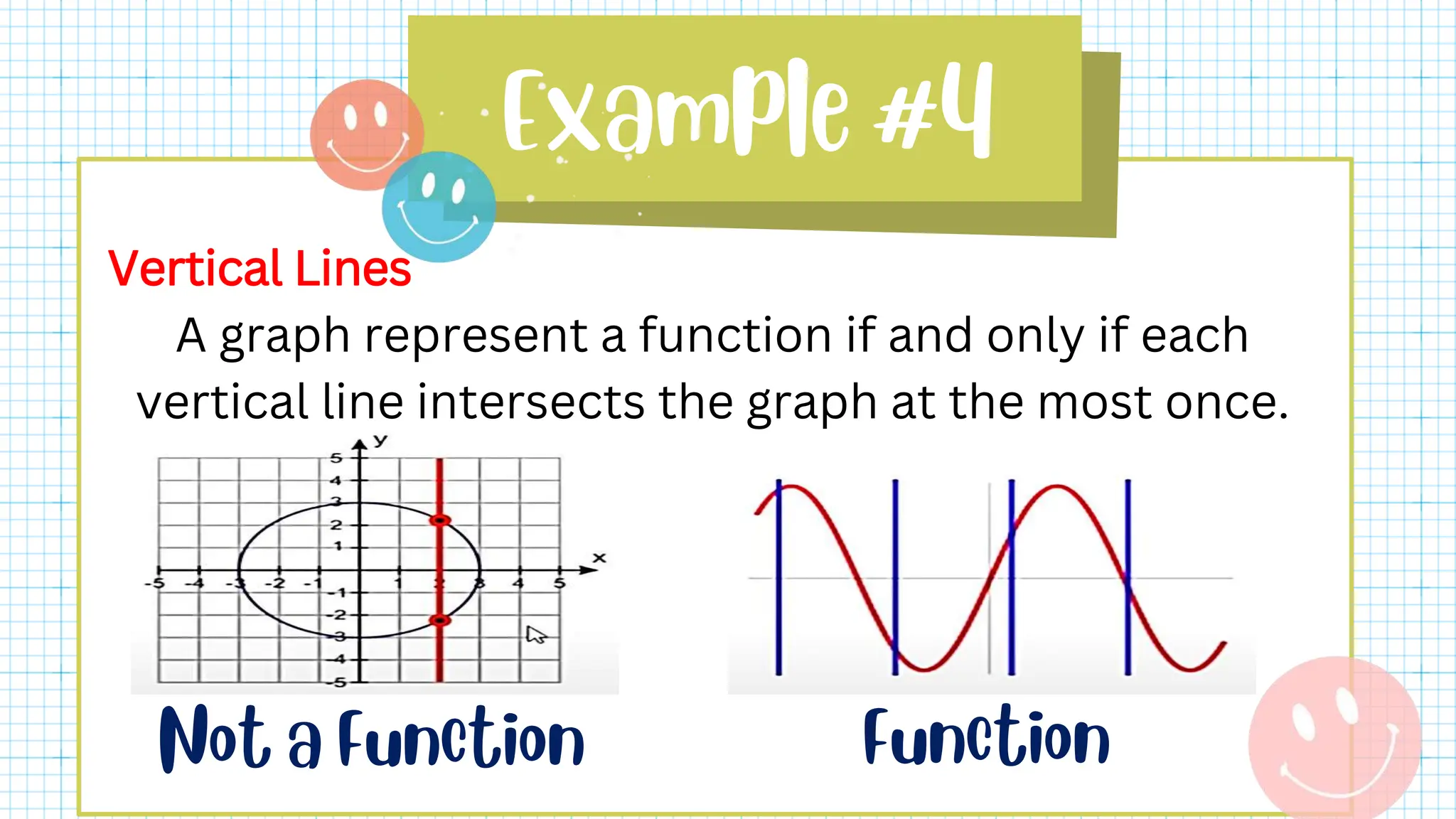
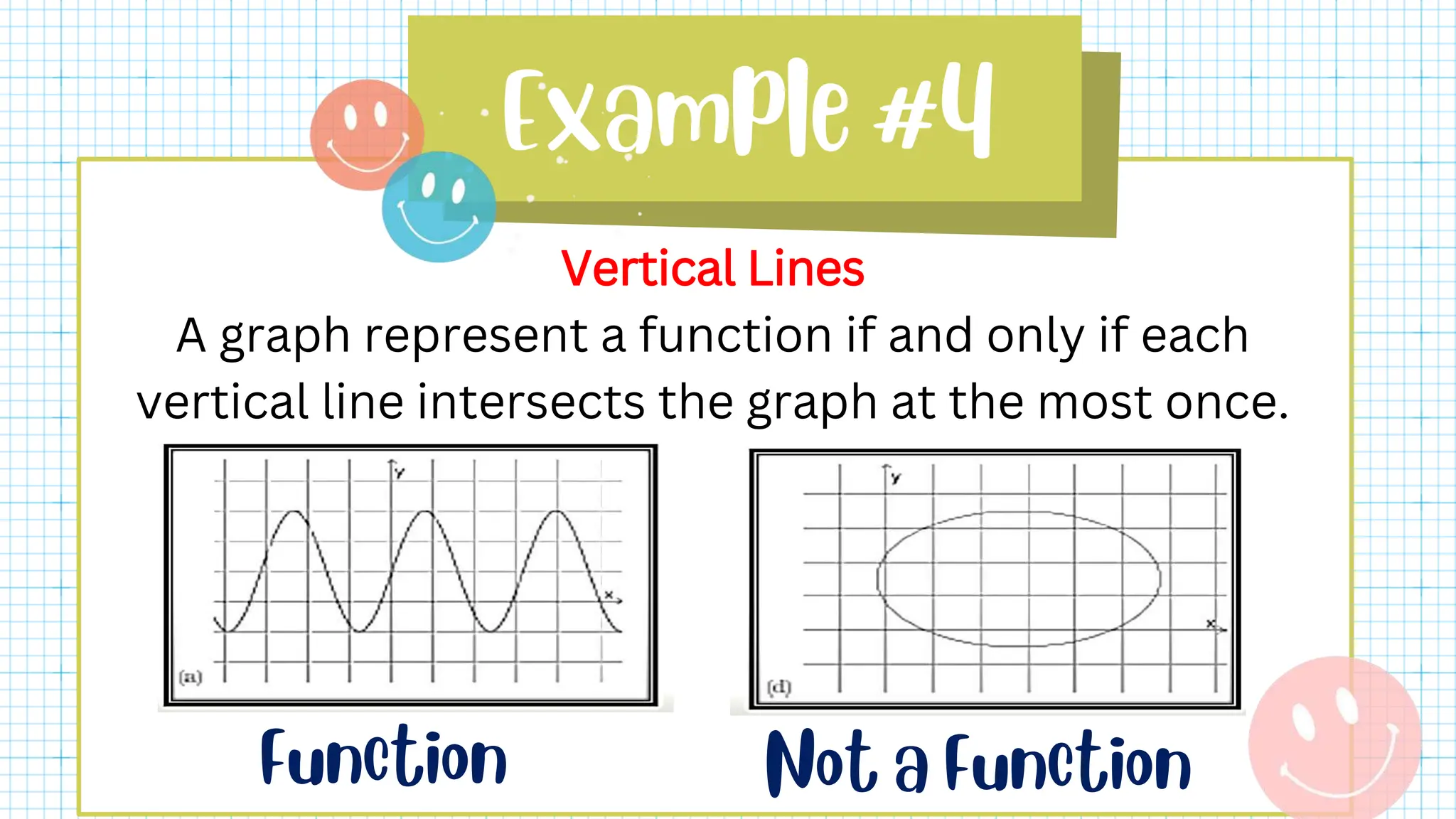
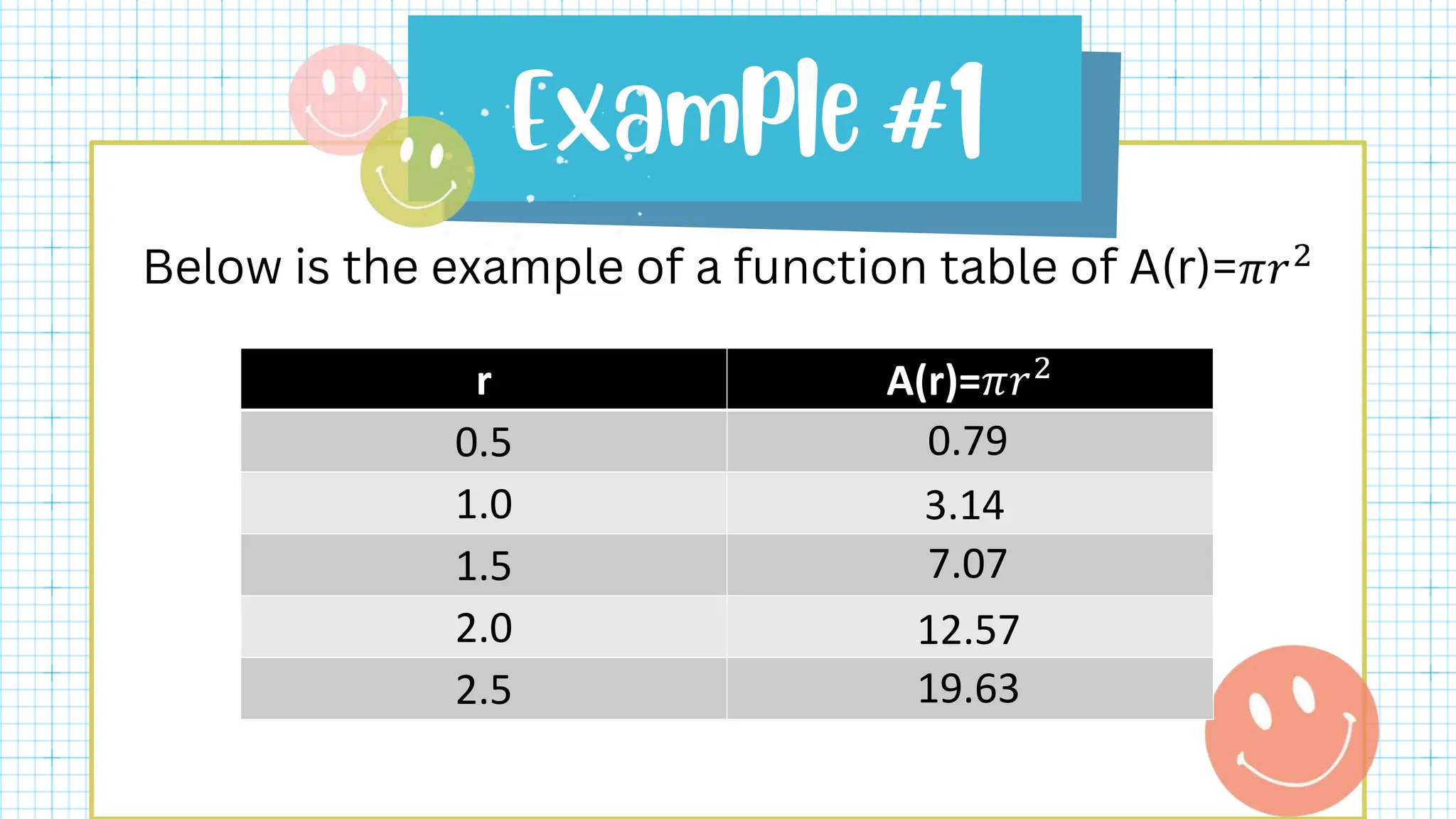
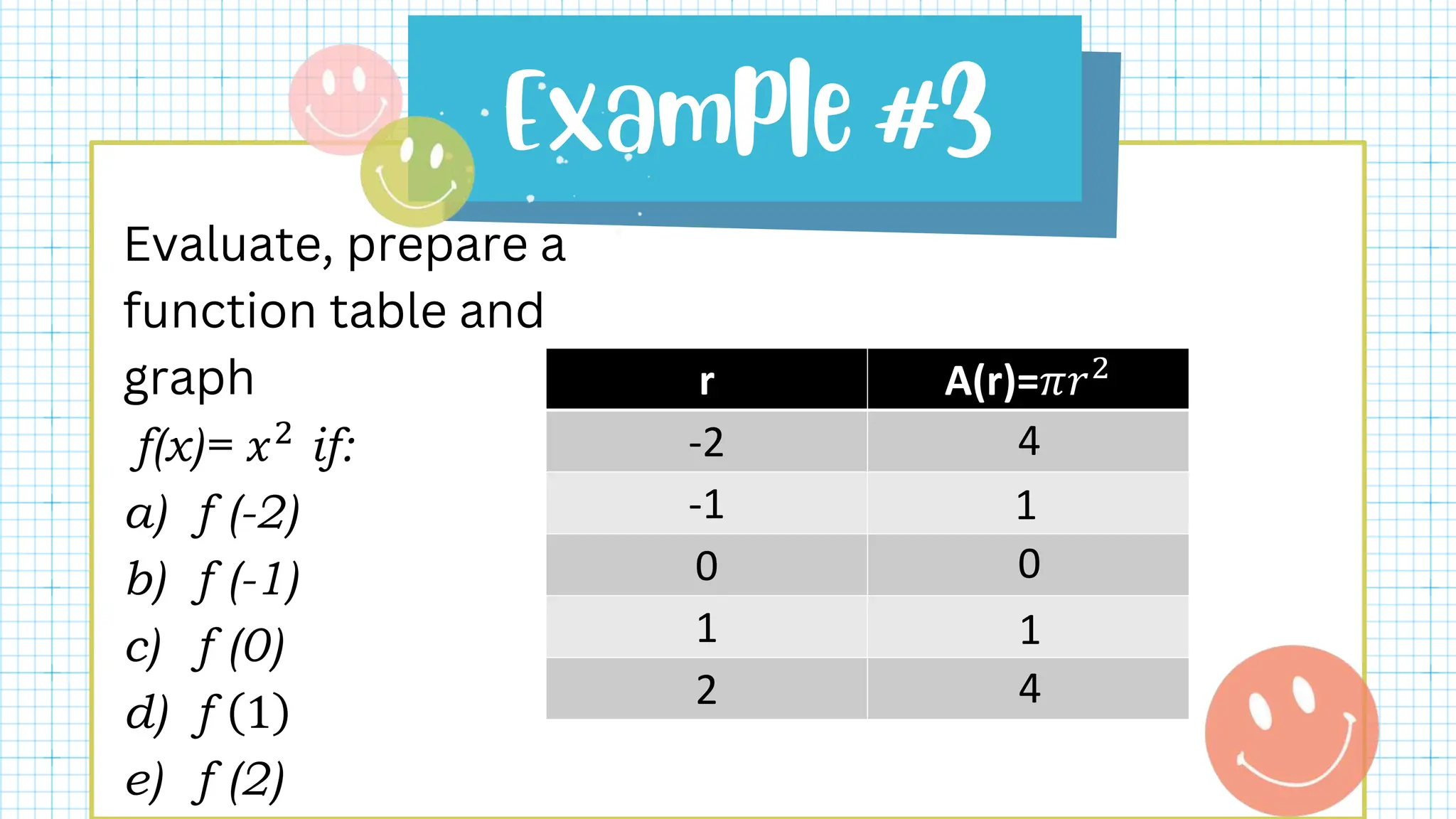
This document defines key terms related to functions such as domain, range, and piecewise functions. It provides examples of representing functions using tables, ordered pairs, graphs, and equations. It also discusses how to determine if a relation represents a function and describes piecewise functions as using more than one formula with separate domains.

2. 1. Define functions and related terms;
2. Determine if the given relation represent a function;
3. Define piecewise function; and
4. represent real life situations using functions, including
piece wise functions.

4. It is the set of first coordinates.
a. Range
b. Domain
c. Abscissa

5. It is a set of second coordinates
a. Range
b. Domain
c. Abscissa

6. Find the domain and range of the given ordered pairs.
{(1, -1), (2, -3),(0, 5), (-1, 3), (4,-5), (-1, 5), (4, -4)}
Domain- {-1, 0, 1, 2, 4}
Range- {-5, -4, -3, -1, 3, 5}

8. is any set of ordered pairs. The set of all first elements of the
ordered pairs is called the domain of the relation, and the set of
all second elements is called the range. Members of these sets
are called elements.
A relation from set A to set B is defined to be any subset
of A x B. if R is a relation from A to B and (a, b) ∈ R, then we
say that “a is related to b” and it is denoted as a R b.

9. A B

10. Functions- is a correspondence between two sets
where each element in the domain, corresponds to
exactly one element in range.
Functions can represent in four ways.
1. A table of values
Example:
2. Ordered pairs
Example: {(-2, 10), (-1, -7), (0, -4), (1, -1), (2, 2)}

11. 3. Graph, and
Example:
4. Equation
Example: y= 3x-4

12. Determine if the following relations are functions or
not function?
f= { (1, 2), (2, 2), (3, 5), (4, 5)}
g= { ( 1, 3), (1, 4), (2, 5) ( 2, 6), (3, 7)}
h= { ( 1, 3), (2, 6), ( 3, 9), …, (n, 3n),… }

13. Determine whether the relationship given in the
mapping diagram is a function or not a function.

14. Determine whether the relationship given in the
mapping diagram is a function or not a function.

15. Vertical Lines
A graph represent a function if and only if each
vertical line intersects the graph at the most once.

16. Vertical Lines
A graph represent a function if and only if each
vertical line intersects the graph at the most once.

17. Which of the following equation describe a function?

18. -Display the inputs and corresponding outputs of a
function. Function Tables can be vertical (up and
down) or horizontal (Side to side)

19. Below is the example of a function table of A(r)=𝜋𝑟2
r A(r)=𝜋𝑟2
0.5
1.0
1.5
2.0
2.5
0.79
3.14
7.07
19.63
12.57

20. Evaluate, prepare a
function table and
graph
f(x)= x+1 if:
a) f (-2)
b) f (-1)
c) f (0)
d) f 1
e) f (2)
X x+1
-2
-1
0
1
2
-1
0
1
3
2

21. Evaluate, prepare a
function table and
graph
f(x)= 3𝑥2
+x-5 if:
a) f(-2)
b) f(0)
c) f(4)
d) f
1
2
x 3𝑥2+x-5
-2
0
4
𝟏
𝟐
5
-5
47
−15
4

22. Evaluate, prepare a
function table and
graph
f(x)= 𝑥2
if:
a) f (-2)
b) f (-1)
c) f (0)
d) f 1
e) f (2)
r A(r)=𝜋𝑟2
-2
-1
0
1
2
4
1
0
4
1

23. -is a function in which more than one formula is used
to define the output. Each formula has its own
domain, and the domain of the function is the
union of all these smaller domains.

24. Evaluate f (x) when a) x=0, b) x=2 and c) x=4
f (x) = x+2 if x<2
2x+1 if x ≥ 2

25. Graph the following equation
f (x) = 2x-5 if x<-2
𝑥2
-3 if x ≥ −2