Embed presentation
Downloaded 18 times

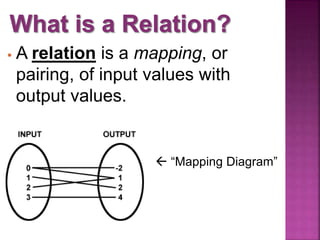
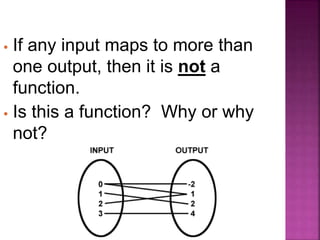
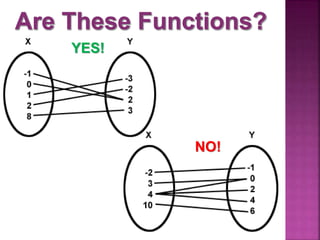
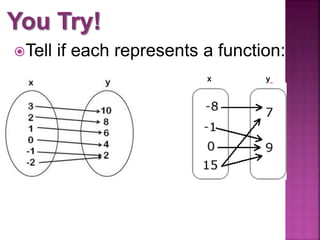



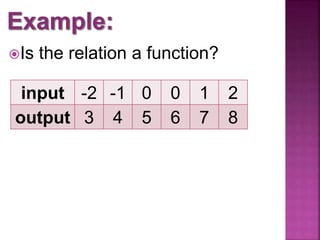
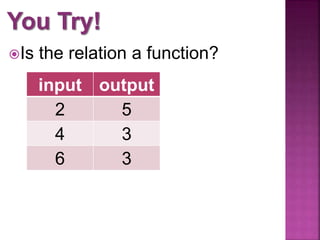
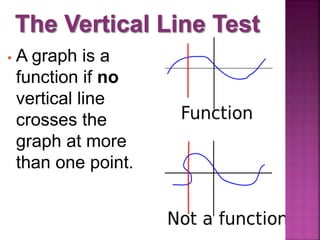
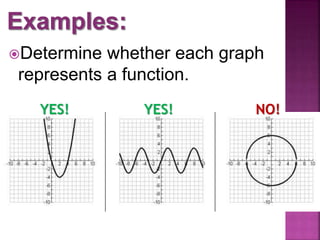
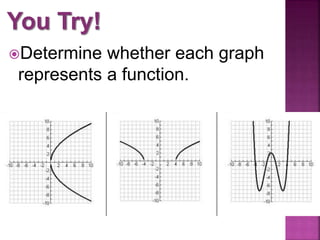
This document discusses functions and relations. It defines a relation as a mapping of inputs to outputs, and specifies that a relation is a function only if each input maps to exactly one output. It then provides examples of relations represented as ordered pairs, tables, graphs, and equations, and asks the reader to determine whether each example represents a function or not.












