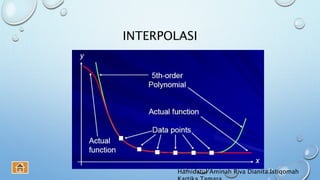
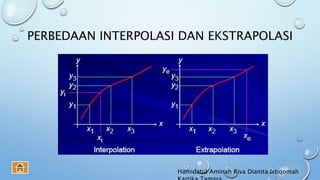
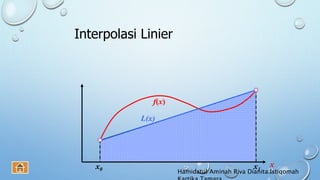
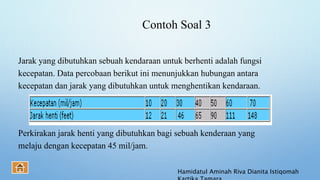
Dokumen ini membahas regresi dan interpolasi, termasuk penjelasan tentang analisis regresi linier dan metode perhitungan koefisien regresi. Regresi linier digunakan untuk memprediksi nilai variabel terikat berdasarkan variabel bebas, sementara interpolasi bertujuan untuk menemukan nilai suatu fungsi di antara titik-titik data yang diberikan. Selain itu, dokumen ini juga membahas berbagai jenis interpolasi polinomial dan metode perhitungannya.