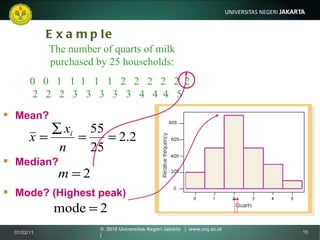
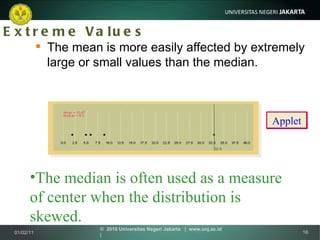
Dokumen ini membahas tentang ukuran-ukuran pemusatan dan lokasi data statistik seperti rata-rata, median, modus, kuartil, desil dan persentil. Metode-metode tersebut digunakan untuk mendeskripsikan letak pusat distribusi data dan membaginya menjadi bagian-bagian yang sama.

1. Pertemuan 4 UKURAN PEMUSATAN DAN LOKASI Hdi Nasbey, M.Si Jurusan Fisika Fakultas Matematika dan Ilmu Pemgetahuan Alam

2. Outline Penyajian Data Beberapa contoh daftar statistic Diagram Batang Diagram garis Diagram lingkaran dan diagram pastel Diagram lambing Diagram peta Diagram Pencar 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

3. Learning Outcomes Pada akhir pertemuan ini, diharapkan mahasiswa akan mampu : Mahasiswa akan dapat menghitung ukuran-ukuran pemusatan dan lokasi. 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

4. Outline Materi Rata-rata Median Modus Kuartil Desil persentil 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

5. Measures of Center A measure along the horizontal axis of the data distribution that locates the center of the distribution. 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

6. 1. Arithmetic Mean or Average The mean of a set of measurements is the sum of the measurements divided by the total number of measurements. where n = number of measurements 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

7. Example The set: 2, 9, 1, 5, 6 If we were able to enumerate the whole population, the population mean would be called   (the Greek letter “ mu ”). 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

8. Mean (Arithmetic Mean) Approximating the Arithmetic Mean Used when raw data are not available 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

9. 2. Median The median of a set of measurements is the middle measurement when the measurements are ranked from smallest to largest . The position of the median is once the measurements have been ordered. a. Md = X (n+1)/2 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | .5( n + 1)

10. Example The set: 2, 4, 9, 8, 6, 5, 3 n = 7 Sort: 2, 3, 4, 5, 6, 8, 9 Position: .5( n + 1) = .5(7 + 1) = 4 th The set: 2, 4, 9, 8, 6, 5 n = 6 Sort: 2, 4, 5, 6, 8, 9 Position: .5( n + 1) = .5(6 + 1) = 3.5 th 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id | Median = 4 th largest measurement Median = (5 + 6)/2 = 5.5 — average of the 3 rd and 4 th measurements

11. b. Median Data Berkelompok 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

12. 3. Mode Untuk menyatakan fenomena yang paling banyak terjadi, juga untuk menentukan “rata-rata” dari data kualitatif. a. Data t ak berkelompok : Modus (Mo) dilihat dari data yang memiliki frekuensi terbanyak The set: 2, 4, 9, 8, 8, 5, 3 The mode is 8 , which occurs twice The set: 2, 2, 9, 8, 8, 5, 3 There are two modes — 8 and 2 ( bimodal ) The set: 2, 4, 9, 8, 5, 3 There is no mode (each value is unique). 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

13. b. Modus Data Berkelompok 4. Kuartil (Q i ) Membagi kelompok data yang telah terurut menjadi 4 bagian yang sama besar. a. Data t ak berkelompok 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

14. b. Kuartil Data Berkelompok 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

15. Example Mean? Median? Mode? (Highest peak) The number of quarts of milk purchased by 25 households: 0 0 1 1 1 1 1 2 2 2 2 2 2 2 2 2 3 3 3 3 3 4 4 4 5 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

16. Extreme Values The mean is more easily affected by extremely large or small values than the median. Applet The median is often used as a measure of center when the distribution is skewed. 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

17. Extreme Values Skewed left: Mean < Median Skewed right: Mean > Median Symmetric: Mean = Median 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

18. 5. Desil Membagi kelompok data yang telah terurut menjadi 10 bagian yang sama besar. a. Data t ak berkelompok b. Data berkelompok 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

19. 6. Persent il (Pi) Membagi kelompok data yang telah terurut menjadi 10 0 bagian yang sama besar. a. Data t ak berkelompok b. Data berkelompok 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |

20. Selamat Belajar Semoga Sukses. 01/02/11 © 2010 Universitas Negeri Jakarta | www.unj.ac.id |