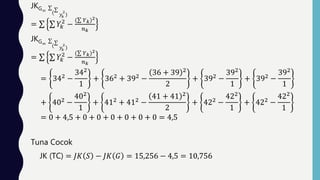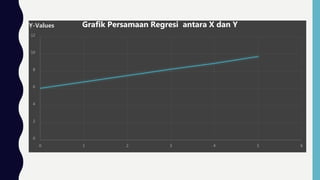
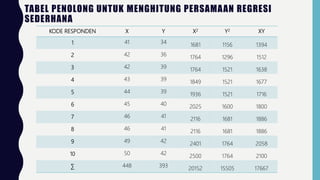
Ringkasan dokumen tersebut adalah: 1. Dokumen tersebut membahas tentang analisis regresi linier sederhana antara satu variabel independen dengan satu variabel dependen. 2. Persamaan umum regresi linier adalah Y = a + bX, dimana a adalah konstanta dan b adalah koefisien regresi. 3. Dokumen tersebut juga menjelaskan cara menghitung nilai a dan b, serta uji signifikansi dan linearitas model regresi menggunakan analisis

1. S TAT I S T I K A
R E G R E S I I I N E A R S E D E R H A N A

2. KELOMPOK
AYDA FITRIANI
TRI HIDAYAH LAILA
VALENTINI
VIRDYA NAMIRA ROCHAIRA

3. Analisis
Regresi
Terdapat
perbedaan
yang mendasar
antara analisis
korelasi dan
regresi.
Analisis korelasi
digunakan untuk
mencari arah dan
kuatnya hubungan
antara dua variabel
atau lebih, baik
hubungan yang b
ersifat simetris,
kausal, dan
reciprocal.
Sedangkan analisis
regresi digunakan untuk
memprediksi seberapa
jauh perubahan nilai
variabel dependen, bila
nilai variabel
independen
dimanipulasi atau
dirubah-rubah atau
dinaik turunkan

4. Regresi sederhana
didasarkan pada
hubungan
fungsional ataupun
kausal satu variabel
independen
dengan satu
variabel dependen.
A. Regresi Linier
Sederhana
Persamaan umum regresi linier
adalah :
𝑌 = a + bX

5. Dimana :
Ý = Subyek dalam variabel dependen yang diprediksikan.
a = Harga Y ketika harga X = 0 (harga konstan)
b = Angka arah atau koefisien regresi, yang menunjukkan angka peningkatan ataupun
penurunan variabel dependen yang didasarkan pada perubahan variabel
independen. Bila (+) arah garis naik, dan bila (-) maka arah garis turun.
X = Subyek pada variabel independen yang mempunyai nilai tertentu.
𝑌 = a + bX

6. LANJUTAN.............
Secara teknis harga b merupakan tangen dari (perbandingan) antara panjang garis
variabel dependen, setelah persamaan regresi ditemukan.
Dimana :
r = Koefisien korelasi product moment antara variabel X dengan variabel Y.
Sy = Simpangan baku variabel Y.
Sx = Simpangan baku variabel X.
Harga b = r
Sy
Sx
Harga a = Y - bX

7. LANJUTAN......
Selain itu harga a dan b dapat dicari dengan rumus berikut :
𝑎 =
( 𝑋2
)( 𝑌) − ( 𝑋)( 𝑋𝑌)
𝑛( 𝑋2) − ( 𝑋)2
b =
𝑛( 𝑋𝑌) − ( 𝑋)( 𝑌)
𝑛( 𝑋2) − ( 𝑋)2

8. Model Regresi sederhana 𝑌 = a +
bX yang diperoleh masih perlu diuji
signifikansinya. Pengujian
signifikansi model regresi dan
kelinearan model regresi
menggunakan teknik ANAVA.
Statistik yang digunakan dalam
ANAVA ialah statistik F.

9. UJI SIGNIFIKANSI
REGRESI
Untuk menguji signifikansi model regresi dalam
ANAVA digunakan nilai F yang diperoleh dari
rumus:
Dimana :
𝑆 𝑟𝑒𝑔
2 adalah variansi regresi atau Jumlah Kuadrat
b/a yang dihitung dari rumus
JKReg = b. 𝑥𝑦 = 𝑏. 𝑋𝑌 −
( 𝑋).( 𝑌)
𝑛
𝑆 𝑠𝑖𝑠
2
adalah variansi sisa jumlah Kuadrat Sisa
yang dihitung dari rumus
JKs=JKT –JKa-JKReg
untuk JKT = 𝑌
2
dan JKa =
( 𝑌)2
𝑛

10. UJI LINEARITAS
REGRESI
Untuk menguji kelinearan model regresi dalam
ANAVA digunakan nilai F yang diperoleh dari
rumus:
Dimana :
𝑆 𝑇𝐶
2
adalah variansi tuna cocok atau Jumlah
Kuadrat TC yang dihitung dari rumus
JK (TC) = 𝐽𝐾 𝑆 − 𝐽𝐾 𝐺
𝑆 𝐺
2
adalah variansi galat atau JKG dihitung dari
rumus
JKG= ( 𝑦 𝑘
2
)
= 𝑌𝑘
2
−
( 𝑌 𝑘)2
𝑛 𝑘

11. CONTOH SOAL
Berikut Data Yang Didapat Dari Penelitian Korelasi Antara Motivasi Dengan
Prestasi Belajar Ipa SD Kelas 5 Di SDN 09 Pagi Petukangan Utara
Siswa X Y
1 41 34
2 42 36
3 42 39
4 43 39
5 44 39
6 45 40
7 46 41
8 46 41
9 49 42
10 50 42
∑ 448 393

12. HIPOTESIS STATISTIK
1. Ho: 𝜌 𝑦𝑥 ≤ 0
H1: 𝜌 𝑦𝑥 > 0
2. Ho: 𝜌 𝑦𝑥 = 0
Ho: 𝜌 𝑦𝑥 ≠ 0

13. KODE RESPONDEN X Y X2 Y2 XY
1 41 34
1681 1156 1394
2 42 36
1764 1296 1512
3 42 39
1764 1521 1638
4 43 39
1849 1521 1677
5 44 39
1936 1521 1716
6 45 40
2025 1600 1800
7 46 41
2116 1681 1886
8 46 41
2116 1681 1886
9 49 42
2401 1764 2058
10 50 42
2500 1764 2100
∑ 448 393
20152 15505 17667
TABEL PENOLONG UNTUK MENGHITUNG PERSAMAAN REGRESI
SEDERHANA

14. PENYELESAIAN
𝑎 =
( 𝑋2
)( 𝑌) − ( 𝑋) ( 𝑋𝑌)
𝑛 𝑋2 − ( 𝑋)
2
𝑎 =
20152.393 − (448.17667)
10 20152 − (448)2
𝑎 =
4920
816
= 6,029
= 6,03
𝑏 =
𝑛 𝑋𝑌 − ( 𝑋) ( 𝑌)
𝑛 𝑋2 − ( 𝑋)
2
𝑏 =
(10. 17667) − (448.393)
(10. 20152) − (448)2
𝑏 =0,742647059
𝑏 =0,74

15. Uji Hipotesis (regresi linear sederhana)
a. Model Regresi
Persamaan Regresi :
𝑌 = 6,03 + 0,74𝑋
Kesimpulan : setiap kenaikan satu skor
X (motivasi) maka prestasi belajar Ipa
akan naik sebesar 0,74 pada
konstanta 6,03

16. • Jumlah kuadrat total (JKT)
JKT = 𝑌
2
= 15505
• Jumlah kuadrat regresi a
(JKa)
JKa =
( 𝑌)2
𝑛
=
(393)2
10
=
154449
10
= 15444,9
• Jumlah kuadrat tereduksi
(JKR)
JKR = JKT ─ JKa atau JKR =
𝑦
2
JKR = 15505 ─ 15444,9 =
60,1
• Jumlah kuadrat regresi b (JKb
atau JKReg)
• JKb = JKReg =
b. 𝑥𝑦 = 𝑏. 𝑋𝑌 −
( 𝑋).( 𝑌)
𝑛
= 0,74 . 17667 −
(448). (393))
10
= 0,74 . 17667 − 17606,4
= 0,74 . 60,6
= 44,844
b. Jumlah Kuadrat (JK) dan derajat
kebebasan

17. Jumlah kuadrat sisa (JKs)
JKs=JKT –JKa-JKReg
=JKR-JKReg
=60,1 − 44,844 = 15,256
Jumlah kuadrat Galat (JKg)
JKG= ( 𝑦 𝑘
2
)
= 𝑌𝑘
2
−
( 𝑌 𝑘)2
𝑛 𝑘
No 1 2 3 4 5 6 7 8 9 1
X
4
1
4
2
4
2
4
3
4
4
4
5
4
6
4
6
4
9
5
0
Y
3
4
3
6
3
9
3
9
3
9
4
0
4
1
4
1
4
2
4
2
K 1 2 3 4 5 6 7 8
G 0 4,5 0 0 0 0 0 0

18. JKG= ( 𝑦𝑘
2
)
= 𝑌𝑘
2
−
( 𝑌 𝑘)2
𝑛 𝑘
JKG= ( 𝑦𝑘
2
)
= 𝑌𝑘
2
−
( 𝑌 𝑘)2
𝑛 𝑘
= 342 −
342
1
+ 362 + 392 −
36 + 39 2
2
+ 392 −
392
1
+ 392 −
392
1
+ 402 −
402
1
+ 412 + 412 −
41 + 41 2
2
+ 422 −
422
1
+ 422 −
422
1
= 0 + 4,5 + 0 + 0 + 0 + 0 + 0 + 0 = 4,5
Tuna Cocok
JK (TC) = 𝐽𝐾 𝑆 − 𝐽𝐾 𝐺 = 15,256 − 4,5 = 10,756

19. UJI SIGNIFIKANSI
Hipotesis:
Ho : 𝜷 𝟏 = 𝟎 𝜷 𝟏 ≤ 𝟎
H1 : 𝜷 𝟏 ≠ 𝟎 𝜷 𝟏 > 𝟎
Pengujian:
𝑭 𝒉 =
𝑺 𝒓𝒆𝒈
𝟐
𝑺 𝒔𝒊𝒔
𝟐
𝑭 𝒉 =
JK 𝑅𝑒𝑔
1
JK 𝑆
𝑛 − 2
=
𝟒𝟒, 𝟖𝟒𝟒
𝟏
𝟏𝟓, 𝟐𝟓𝟔
𝟖
= 𝟐𝟑, 𝟓𝟐
Karena :
Fh= 23,52>Ft (0,05) =5,32
Fh= 23,52>Ft (0,01) =11,26
Maka Ho ditolak berarti (koefisien) regresi sangat signifikan

20. Hipotesis:
Ho : 𝒀 = 𝒂 𝟏 + 𝜷 𝟏 𝑿 𝟏
H1 : 𝒀 ≠ 𝒂 𝟏 + 𝜷 𝟏 𝑿 𝟏
Pengujian:
𝑭 𝒉 =
𝑺 𝑻𝑪
𝟐
𝑺 𝑮
𝟐
𝑭 𝒉 =
JK TC
𝑘 − 2
JK 𝐺
𝑛 − 𝑘
=
𝟏𝟎, 𝟕𝟓𝟔
𝟔
𝟒, 𝟓
𝟐
=
𝟏, 𝟕𝟗𝟑
𝟐, 𝟐𝟓
= 𝟎, 𝟕𝟗𝟕
Karena :
Fh= 0,797>Ft (0,05) =19,33
Fh= 0,797>Ft (0,01) =99,33
Maka Ho diterima berarti regresi linear
UJI LINEARITAS

21. 0
2
4
6
8
10
12
0 1 2 3 4 5 6
Y-Values Grafik Persamaan Regresi antara X dan Y

22. DAFTAR PUSTAKA
Kusdiwelirawan, A. 2013. Statistik Pendidikan. Jakarta: Uhamka PRESS
Sugiyono. 2010. Statistika untuk Penelitian. Bandung: Alfabeta.