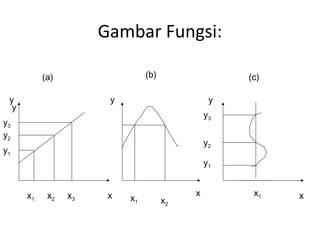
Dokumen ini membahas definisi dan konsep dasar fungsi matematis, termasuk variabel, koefisien, dan konstanta serta sifat-sifat variabel seperti variabel terikat dan bebas. Selain itu, dokumen ini menjelaskan jenis-jenis persamaan, cara menggambarkan fungsi linear, dan pencarian akar-akar persamaan linear. Dimasukkan pula analisis biaya total, penerimaan total, dan fungsi anggaran dalam konteks ekonomi.

1. FUNGSI LINEAR
IMELDA
imelda all right's reserved

2. FUNGSI
• DEFENISI FUNGSI :
Suatu bentuk hubungan matematis yang
menyatakan hubungan ketergantungan
(hubungan fungsional) antara satu variabel
dengan variabel lainnya
imelda all right's reserved

3. CONTOH : y = f (x),
dibaca “Y adalah sama dengan fungsi dari X”
• menyatakan hubungan antara 2 variabel yaitu
variabel y & x.
• Hubungan di antara variabel x dan y mengharuskan
adanya satu nilai y yang unik untuk setiap nilai x,
tetapi hal yang sebaliknya tidak diharuskan.
• Jadi lebih dari satu nilai x dapat dihubungkan dengan
nilai y yang sama, tetapi sebaliknya beberapa nilai y
tidak dapat dihubungkan dengan nilai x yang sama.
imelda all right's reserved

4. Gambar Fungsi:
(a) (b) (c)
y y y
y
y3
y3
y2
y2
y1
y1
x1 x2 x3 x x x1 x
x1 x2

5. UNSUR FUNGSI ADA 3:
1. VARIABEL
2. KOEFISIEN
3. KONSTANTA
VARIABEL & KOEFISIEN : Selalu Ada Pada Setiap
Bentuk Fungsi
KONSTANTA : Belum Tentu Ada
imelda all right's reserved

6. VARIABEL (PEUBAH)
• Sesuatu yang besarnya dapat berubah, misalnya
sesuatu yang dapat menerima nilai yang berbeda
• Menggambarkan atau mewakili suatu faktor tertentu
• Ditulis dengan huruf latin
(Huruf Kecil): x, y, z, p, q, c, i
• Melambangkan sumbu dalam sistem koordinat
imelda all right's reserved

7. Contoh Variabel
• Variabel dalam matematika ekonomi sering
dilambangkan dengan huruf yang ada di
depan nama variabel tersebut.
• P = Price (Harga)
• Q = Quantity (jumlah yang
ditawarkan/diminta)
• C = Cost (Biaya)
• I = Investment (Investasi)
imelda all right's reserved

8. SIFAT VARIABEL
• VARIABEL TERIKAT (DEPENDENT VARIABLE) :
Nilai variabel tergantung atau ditentukan oleh variabel lain.  Variabel Endogen : suatu
variabel yang nilai penyelesaiannya diperoleh dari dalam model.
• VARIABEL BEBAS (INDEPENDENT VARIABLE):
Nilai variabel tidak tergantung pada variabel lain. -> Variabel Eksogen : suatu variabel yang yang
nilainya diperoleh dari luar model dan nilai-nilai variabel yang diperoleh dari data yang ada.
y = f (x)
y : variabel terikat/dependent variable/variabel endogen
x : variabel bebas/independent variable/variabel eksogen
Ingat !!! Suatu variabel mungkin merupakan variabel endogen pada suatu model dan mungkin juga
merupakan variabel eksogen pada model lainnya. Contoh : Pada analisa penentuan harga dan
jumlah keseimbangan pasar suatu barang, harga adalah variabel endogen tapi dalam
penentuan pengeluaran konsumen maka variabel p adalah variabel eksogen karena p
merupakan data konsumen perorangan.
imelda all right's reserved

9. KOEFISIEN & KONSTANTA
• KONSTANTA : Bilangan atau angka yang (kadang-kadang) turut membentuk suatu fungsi tetapi berdiri
sendiri sebagai bilangan & tidak terkait pada suatu variabel tertentu
• KONSTANTA : KUANTITAS YANG NILAIINYA TIDAK BERUBAH DALAM SUATU MASALAH TERTENTU. Jika
suatu konstanta digabung dengan sebuah variabel, maka angka itu sering disebut dengan koefisien.
• KOEFISIEN : Bilangan atau angka yang terkait pada & terletak di depan suatu variabel dalam sebuah fungsi
• KONSTANTA BILANGAN (NUMERICAL CONSTANT) : MEMPUNYAI NILAI YANG SAMA DALAM SEMUA SOAL.
• KONSTANTA SIMBOLIK (SYMBOLIC CONSTANT ATAU PARAMETER) : MEMPUNYAI NILAI YANG SAMA
DALAM SOAL TERTENTU TETAPI DAPAT MEMPUNYAI NILAI YANG LAIN DALAM SOAL YANG BERBEDA.
(misalnya: aP sebagai pengganti 0,7P)
Konstanta Parameter biasanya dinyatakan dengan simbol a, b, c atau
dalam abjad Yunani
• NOTASI FUNGSI UMUM: y = f (x) αβσ
• Contoh : y = 5 + 0,7 x atau
f (x) = 5 + 0,7 x
imelda all right's reserved

10. 3 Macam Persamaan
• Variabel dapat berdiri sendiri, tetapi mempunyai arti jika berhubungan satu dengan
yang lain melalui persamaan dan ketidaksamaan.
• 3 Macam Persamaan
– Definitional Equation : membentuk identitas di antara dua pernyataan yang mempunyai
arti yang persis sama. Persamaan ini disebut dengan persamaan identik.
Contoh :
GNP = C + I + G + (X-M)
– Behavioral Equation : menunjukkan perubahan perilaku suatu variabel sebagai akibat dari
perubahan variabel lainnya, yang ada hubungannya.
Contoh : Perubahan perilaku perusahaan, misalnya perubahan biaya total dari suatu
perusahaan sebagai akibat dari perubahan jumlah produksi (TC = 100 + 25 Q)
– Equilibrium Equation : menggambarkan prasyarat untuk pencapaian keseimbangan
(equilibrium).
Contoh : Model keseimbangan pasar ; Qd = Qs
Model keseimbangan pendapatan nasional ; S = I
imelda all right's reserved

11. Fungsi Umum VS Fungsi Khusus
• Fungsi Umum (General Function) :
Menyebutkan semua variabel bebas yang mempengaruhi
variabel terikat, akan tetapi tidak memberi penjelasan
apapun mengenai bagaimana variabel bebas tersebut
mempengaruhi variabel terikat
Contoh : y = f (x), Qd = f (p, Y, pj, T)
• Fungsi Khusus (Specific Function) :
Mencatat argumen-argumen & bagaimana variabel bebas
mempengaruhi variabel terikat
Contoh : Qd = 250 – 5 p + 0,03 Y + pj + 0,02 T
imelda all right's reserved

12. JENIS FUNGSI
• Fungsi Linear • Fungsi Non Linear
(Fungsi berderajat 1) Pangkat tertinggi > 1
Pangkat tertinggi dari  Fungsi Kuadrat :
variabelnya = 1 y = a + bx + cx2
Contoh :  Fungsi Kubik
y = a + bx y = a + bx + cx2 + dx3
imelda all right's reserved

13. JENIS FUNGSI BERDASARKAN LETAK RUAS
VARIABELNYA
• FUNGSI EKSPLISIT • FUNGSI IMPLISIT
Fungsi yang variabel bebas & Fungsi yang variabel bebas &
variabel terikatnya terletak variabel terikatnya terletak
di ruas yang berbeda di ruas yang sama sehingga
sehingga dapat dengan jelas tidak mudah dapat
dibedakan. dibedakan.
y = f (x) 0 = f (x,y)
y = a 0 + a1 x 0 = a0 + a1 x - y
y = a 0 + a 1 x + a 2x2 0 = a 0 + a 1 x + a 2x2 - y
y = a0 + a1 x + a2x2 +a3x3 0 = a0 + a1 x + a2x2 +a3x3-y
imelda all right's reserved

14. PENGGAMBARAN FUNGSI LINEAR
• Hasil berupa garis lurus
• Cara : menghitung koordinat titik-titik yang
memenuhi persamaannya kemudian memindahkan
pasangan-pasangan titik ke sistem koordinat (sumbu
silang)
• Sumbu horisontal (absis) : x
• Sumbu vertikal (ordinat) : y
• y=3+2x ; y = 2x
x=0 1 2 3 4 x=0 1 2 3 4
y = 3 5 7 9 11 y=0 2 4 6 8
imelda all right's reserved

15. PENGGAMBARAN FUNGSI LINEAR
• y=a+bx
• y = 3 + 2x
• y = 8 – 2x
a = konstanta = penggal (intercept) garis pada sumbu vertikal y = titik dimana grafik
memotong sumbu vertikal y = terjadi jika variabel bebas x sama dengan nol. (Nilai y
pada x = 0).
Untuk: Y = bx atau a=0, contoh : y = 2 x, maka garis (grafik) tidak mempunyai penggal
pada sumbu vertikal = garis bermula dari titik (0,0).
b = koefisien = arah = lereng garis = kemiringan (slope) garis mengukur perubahan
nilai variabel pada sumbu vertikal dibagi dengan nilai variabel pada sumbu
horisontal = ^y/^x.
b = mencerminkan besarnya tambahan nilai y untuk setiap tambahan satu nilai x
b > 0 : garis bergerak dari kiri bawah ke kanan atas
b < 0 : garis bergerak dari kiri atas ke kanan bawah
imelda all right's reserved

16. • y = a -> b = 0 • x=c
• Garis lurus sejajar • Garis lurus sejajar
sumbu horisontal x sumbu vertikal y
• Besar kecilnya nilai x • Besar kecilnya nilai y
tidak mempengaruhi tidak mempengaruhi
nilai y nilai x
y
y
x c x
imelda all right's reserved

17. PEMBENTUKAN PERSAMAAN LINEAR
• Dwi-koordinat ;
diketahui 2 titik A (x1,y1)& B (x2, y2)
y – y1 = x – x1
y 2 – y 1 x2 – x 1
Contoh : A (2,3) dan B (6,5)
• Koordinat-lereng
diketahui lereng b dan titik koordinat (x1,y1)
y – y1 = b (x – x1)
Contoh : b = 0,5 dan A (2,3)
• Penggal-lereng
diketahui intersep dan koefisien: y = a + bx
Contoh : a= 3 dan b = 0,4
• Dwi-penggal
diketahui penggal vertikal dan penggal horisontal
y=a– a x
c
a = penggal vertikal dan b = penggal horisontal
imelda all right's reserved
Contoh : a = 2 dan c = -4

18. LERENG
• LERENG adalah hasil bagi selisih antara dua ordinat (y2 –y1)
terhadap Selisih Antara Dua Absis (x2 – x1).
Cara Dwi Koordinat :
y – y 1 = x – x1
y 2 – y 1 x2 – x 1
y – y1 = y2 – y1 (x – x1)
(x2 – x1)
Cara Koordinat Lereng :
y – y1 = b (x – x1)
b = y2 – y 1
x2 – x1
imelda all right's reserved

19. HUBUNGAN DUA GARIS LURUS
• BERIMPIT
y1= ny2 ; a1 = na2 ; b1 = nb2
• SEJAJAR
≠
a1 a2 ; b1 = b2
• BERPOTONGAN
≠
b1 b2
• TEGAK LURUS
b 1 = -1/b2
imelda all right's reserved

20. Sejajar :a1 ≠ a2 ; b1 = b2
Berimpit y1= ny2 ; a1 = na2 ;
b1 = nb2
y y b 1X
b 1X =a
1 +
=a 1 Y
+
1
Y1
b 2X
=a 2 b 2X
+
Y2 = a2
+
Y 2
x 0 x
0
y y
X
b 1X b1
=a
+ +
1
a1 Y
Y1 =
Y1 2 =
a
Y2 = a 2 + b2X 2
+ b
2 X
0 0 x
x
Berpotongan b1 ≠ b2 Tegak Lurus : b 1 = -1/b2
imelda all right's reserved

21. PENCARIAN AKAR-AKAR PERSAMAAN
LINEAR
• SUBSITUSI
• ELIMINASI
• DETERMINAN
imelda all right's reserved

22. SUBSITUSI
• Dua persamaan dengan 2 bilangan anu dapat
diselesaikan dengan cara menyelesaikan
terlebih dahulu sebuah persamaan untuk
salah satu bilangan anu, kemudian
mensubsitusikannya ke dalam persamaan lain.
• Contoh : 2x + 3y = 21 dan x + 4y = 23
imelda all right's reserved

23. ELIMINASI
• Dua persamaan dengan 2 bilangan anu dapat
diselesaikan dengan cara menghilangkan
untuk sementara (mengeliminasi) salah satu
dari bilangan anu yang ada, sehingga dapat
dihitung nilai dari bilangan anu yang lain.
• Contoh : 2x + 3y = 21 dan x + 4y = 23
imelda all right's reserved

24. LATIHAN:
“PRACTICES MAKE PERFECT”
• Diketahui dua pasang persamaan:
1) Qd = a + bP
Qs = c + dP
2) S = -50 + 0,3 Y
I = 250 – 0,2 i
Tentukan :
a. konstanta baik bilangan maupun parametrik
b. Variabel bebas dan terikat
c. koefisien
imelda all right's reserved

25. Nyatakan masing-masing pernyataan berikut
dalam notasi fungsi umum dan khusus:
• Total cost (TC) sebagai fungsi jumlah tenaga
kerja (L) yang diperkerjakan dan jumlah modal
(K) yang digunakan, apabila harga tenaga kerja
Rp 3,- dan harga modal Rp 5,-
• Total revenue (TR) sebagai fungsi output (Q),
jika Pq = 5
• Biaya gaji harian (w) untuk tenaga kerja (L)
sebagai fungsi L. Jika PL = 42,50 sehari.
imelda all right's reserved

26. Biaya Total (Total Cost)
• Biaya total yang dikeluarkan oleh sebuah perusahaan dalam operasional
bisnisnya terdiri atas biaya tetap (fixed cost = FC) dan biaya variabel
(variable cost = VC)
• Biaya tetap : tidak tergantung pada jumlah barang yang dihasilkan,
sehingga biaya ini tidak berubah (konstan) walaupun berapa banyak pun
barang yang dihasilkandalam suatu skala tertentu. Biaya tetap berupa
konstanta, kurva berbentuk garis lurus sejajar dengan sumbu horisontal q
(jumlah yang dihasilkan).
• Biaya variabel : tergantung pada jumlah barang yang dihasilkan (semakin
banyak jumlah barang yang dihasilkan maka semakin besar biayanya).
Biaya variabel merupakan fungsi dari jumlah barang yang dihasilkan, kurva
berbentuk garis lurus berlereng positif dan bermula dari titik nol.
imelda all right's reserved

27. Fungsi Biaya Total
• FC = k
• VC = f (Q) = vQ
• TC = C = FC + VC = k + vQ
C = k + vQ
C
VC = vQ
FC = k
0
imelda all right's reserved Q

28. Biaya Rata-rata (Avarege Cost = AC)
• AFC = FC / Q
• AVC = VC / Q
• AC = TC / Q
imelda all right's reserved

29. Penerimaan Total (Total Revenue)
• Penerimaan total merupakan fungsi dari jumlah
produk yang dijual
• TR = R = f (Q)
R=Q.P
Q = R / P (Jumlah barang yang terjual)
• Penerimaan Rata-rata (AR)
AR = R / Q maka AR = R / Q = R / Q = P
AR = P
imelda all right's reserved

30. Analisis Pulang Pokok (Break Even
Point Analysis) = Titik Impas
• BEP = Tingkat jumlah produk (Q) dimana penerimaan
total dari hasil penjualan hanya cukup untuk
menutupi biaya produksi yang dikeluarkan
perusahaan.
• Profit : TR > TC ; > 0 π R
• Rugi : TR < TC ; < 0 π C, R C
BEP
V
C
F
C
imelda all right's reserved
Q

31. BEP
• Profit = TR – TC
• TR = TC
PQ = FC + VC
PQ = FC + vQ
PQ – vQ = FC
Q (P – v) = FC
Q = FC / (P-v) atau QBEP = QE = FC / (P-v)
imelda all right's reserved

32. Contoh:
• Dalam acara “Bubar”, SFC sepakat untuk melayani 100 anggota suporter SFC pada
menu seharga Rp 15 per orang dan setiap tamu tambahan pada harga Rp 20 per
orang.
a) Nyatakan biaya C dari perjamuan “Bubar” sebagai suatu fungsi dari tamu
(suporter) G.
b) Identifikasi variabel tak bebas dan variabel bebas.
c) Gambarkan fungsi tersebut dalam grafik.
• Suatu perusahaan menghasilkan produk dengan biaya variabel per unit Rp 4.000,-
dan harga jualnya per unit Rp 12.000,-. Biaya tetap sebesar Rp 2.000.000,-.
Tentukanlah jumlah per unit produk yang harus perusahaan jual agar mencapai
pulang pokok?
• Biaya total yang dikeluarkan perusahaan ditunjukkan oleh persamaan TC = 15.000
+ 25Q dan penerimaan total TR = 100Q. Pada tingkat produksi berapa unit
perusahaan ini berada dalam kondisi pulang pokok ? Hitung berapa
keuntungan/kerugian perusahaan? Apa yang terjadi jika perusahaan berproduksi
sebanyak 100 dan 300 unit?
imelda all right's reserved

33. Fungsi Anggaran
• Teori Konsumen • Teori Produsen
• Batas maksimum • Batas maksimum
kemampuan seorang kemampuan seorang
konsumen membeli dua produsen dalam
macam output atau lebih menggunakan dua macam
berkenaan dengan jumlah input (atau lebih)
pendapatannya dan harga berkenaan dengan jumlah
masing-masing output dana yang dimiliki dan
• Gambar fungsi anggaran harga masing-masing input
disebut Budget Line • Gambar fungsi anggaran
• M = x. Px + y . Py disebut isocost
• M = x. Px + y . Py
imelda all right's reserved

34. Contoh:
• Bentuklah persamaan anggaran seorang konsumen
untuk topi dan jaket. Jika uang yang dimilikinya
sebesar Rp 500.000,-, sedangkan harga topi dan jaket
masing-masing Rp 10.000,- dan Rp 50.000,- per unit.
Jika semua uangnya dianggarkan dibelanjakan untuk
jaket, berapa jaket yang dapat dibeli? Berapa unit
topi dapat dibeli jika ia hanya membeli jaket
sebanyak 6 unit?
imelda all right's reserved

35. Fungsi Konsumsi : menjelaskan hubungan
konsumsi dan pendapatan nasional
• Ekonomi makro -> Pendapatan masyarakat sebuah negara secara keseluruhan
(pendapatan nasional = Y) dialokasikan ke dua kategori pengeluaran yaitu konsumsi (C)
dan tabungan (S):
Y=C+S
• Fungsi Konsumsi (C) : C = Co + c Y
• C = f (Y) -> Konsumsi berhubungan dengan pendapatan yang dapat dibelanjakan {(C = f
Yd)}
• Co = Autonomous Consumptions = Konsumsi nasional pada saat pendapatan nasional
sebesar nol. Pada konsumsi individu, maka C = C o+ c Yd. a = sejumlah konsumsi mutlak
(absolut) tertentu untuk mempertahankan hidup walaupun tidak mempunyai
pendapatan uang.
• Secara grafik Co= penggal kurva (intersep) pada sumbu vertikal C.
• c = koefisien = mencerminkan besarnya tambahan konsumsi sebagai akibat adanya
tambahan pendapatan nasional sejumlah tertentu.
• c = MPC = marginal propencity to consume = kecenderungan konsumsi marjinal =
∆ ∆ ∆ ∆
C / Y = bernilai positif dan kurang dari satu = 0 < C / Y < 1
imelda all right's reserved

36. Fungsi Tabungan : menjelaskan hubungan
tabungan dan pendapatan nasional
• S = S0 + sY
• Y ∆
s = MPS = marginal propencity to save = S / ∆ = lereng dari kurva tabungan
• S0 = tabungan autonomous = penggal kurva tabungan pada sumbu vertikal S.
• Y=C+S
Y = (C0+ cY ) + S
S = Y – (C0+ c Y) atau C, C= Y
S = -C0+ Y – cY S Saving
S = -C0 + (1 – c) Y C
S0+ sY = S = -C0+ (1- c) Y
Y
Jadi : S0 = -C0
S
s = 1- c  c + s = 1
MPS = 1 – MPC  MPC + MPS = 1
Dissaving
Ye
Y
imelda all right's reserved

37. Contoh
• Jika fungsi konsumsi ditunjukkan oleh
persamaan C = 15 + 0,75 Y. Pendapatan yang
dapat dibelanjakan adalah Rp 30 miliar.
Berapa nilai konsumsi agregat ? Berapa besar
keseimbangan pendapatan nasional?
Gambarkan fungsi konsumsi dan tabungan
nasional secara bersama-sama.
imelda all right's reserved

38. Angka Pengganda (multiplier)
• Suatu bilangan yang menjelaskan tambahan pendapatan
nasional sebagai akibat adanya perubahan pada variabel-
variabel tertentu dalam perekonomian.
• Angka pengganda paling sederhana:
k = 1 / (1-c) = 1 / s
MPS = 0,25 , jadi k = 4 berarti bahwa apabila variabel ekonomi
tertentu misalnya investasi atau pengeluaran pemerintah -
ditambah sejumlah tertentu, maka pendapatan nasional akan
bertambah sebesar 4 kali tambahan variabel tadi.
imelda all right's reserved

39. Pendapatan Disponsible (Yd)
• Yd = Y – T + R
• T : Tax = Pajak
• R : Transfer Payment = Pembayaran Alihan
• C = f (Yd) S = g (Yd) dan
= C0+ c Yd = S0 + s Y d
C + S = Yd
imelda all right's reserved

40. Soal
• Fungsi Konsumsi masyarakat negara EP08
ditunjukkan oleh C = 30 + 0,8 Yd. Jika
pemerintah menerima dari masyarakat
pembayaran pajak sebesar 16 dan pada tahun
yang sama pemerintah memberikan transfer
payment sebesar 6, berapa konsumsi nasional
seandainya pendapatan nasional pada tahun
tersebut sebesar 200? Hitung besarnya
tabungan nasional?
imelda all right's reserved

41. Fungsi Pajak
• T = T0 (Pajak yang jumlahnya tertentu, tidak dikaitkan dengan
pendapatan, kurva berupa garis lurus sejajar dengan sumbu
pendapatan)
• T = tY (Pajak yang dikaitkan dengan tingkat pendapatan, besarnya
merupakan proporsi atau persentase tertentu dari pendapatan,
kurva sebuah garis lurus berlereng positif dan bermula dari titik
pangkal)
• T = T0 + tY (Besar pajak yang diterima pemerintah)
tY
+
T T0
T=
T= tY
T0
imelda all right's reserved
Y