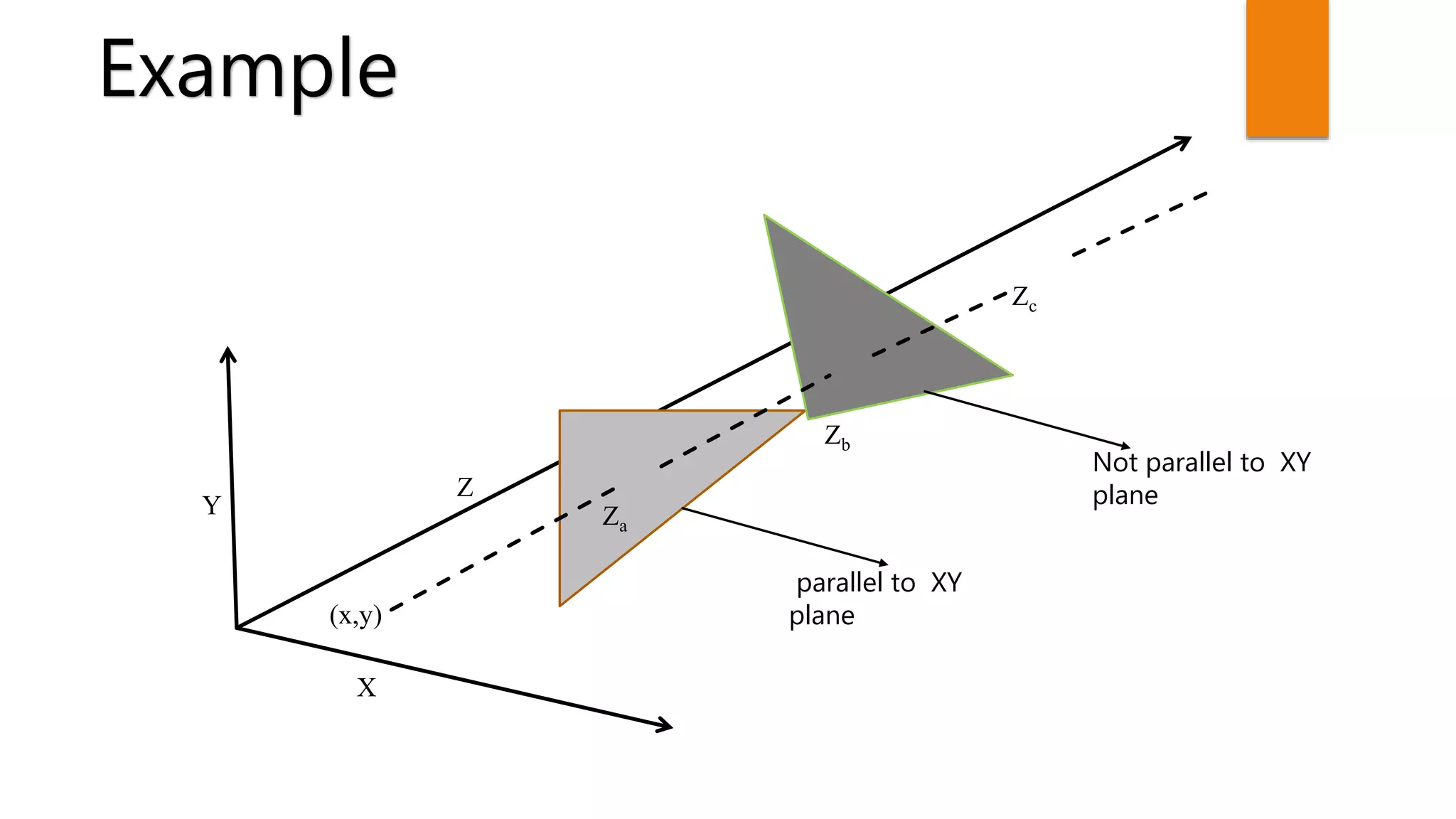
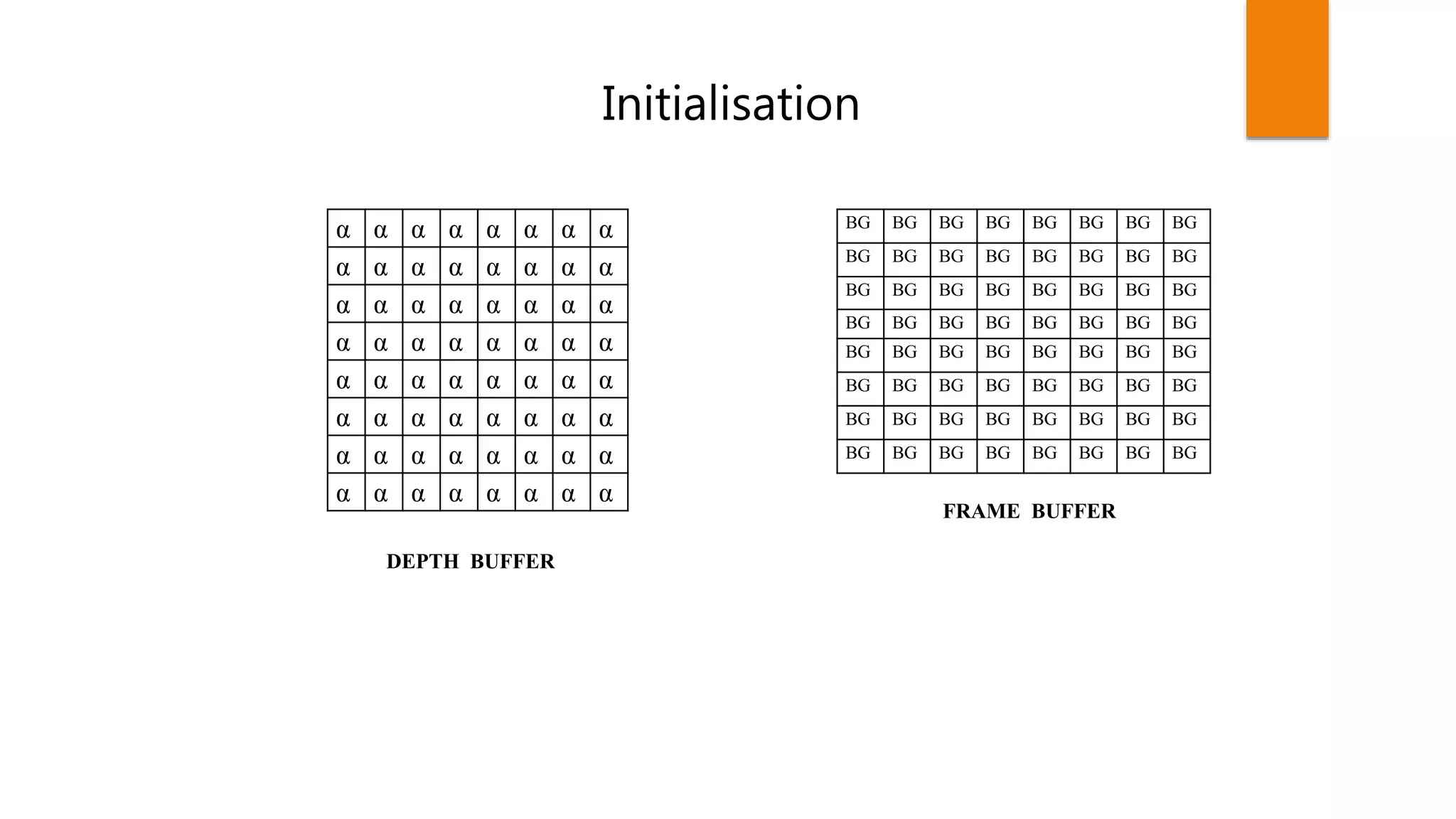
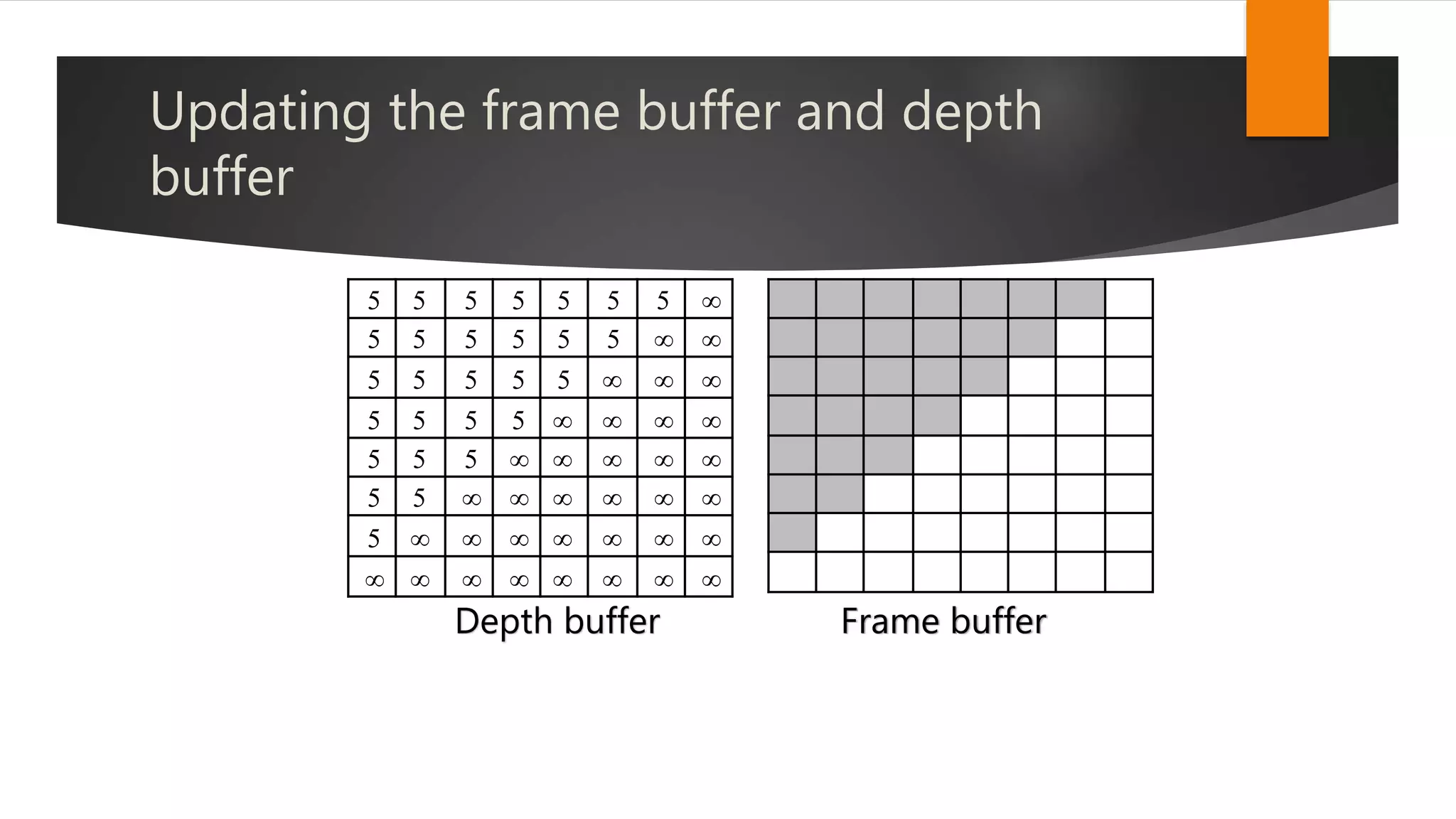
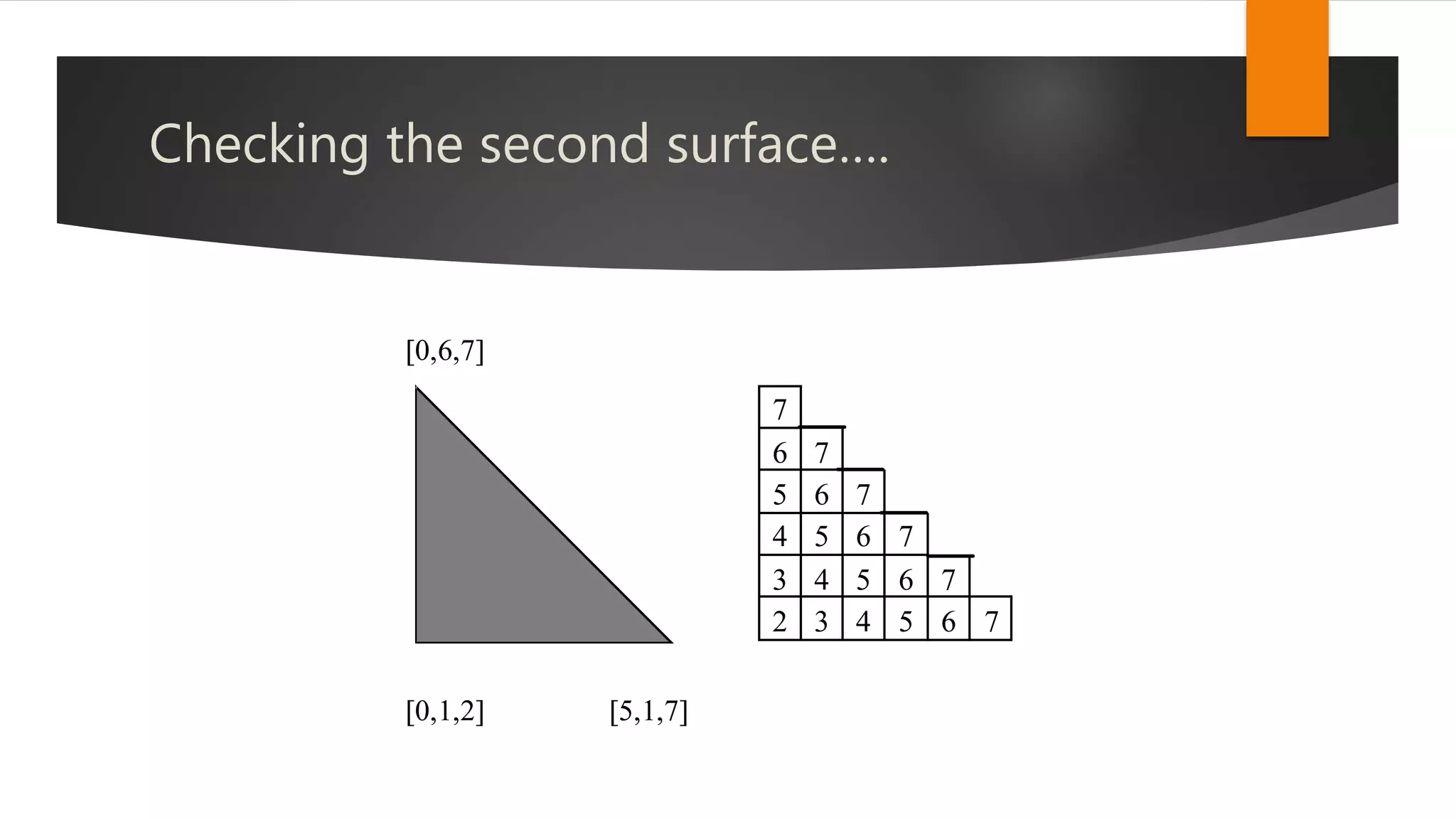
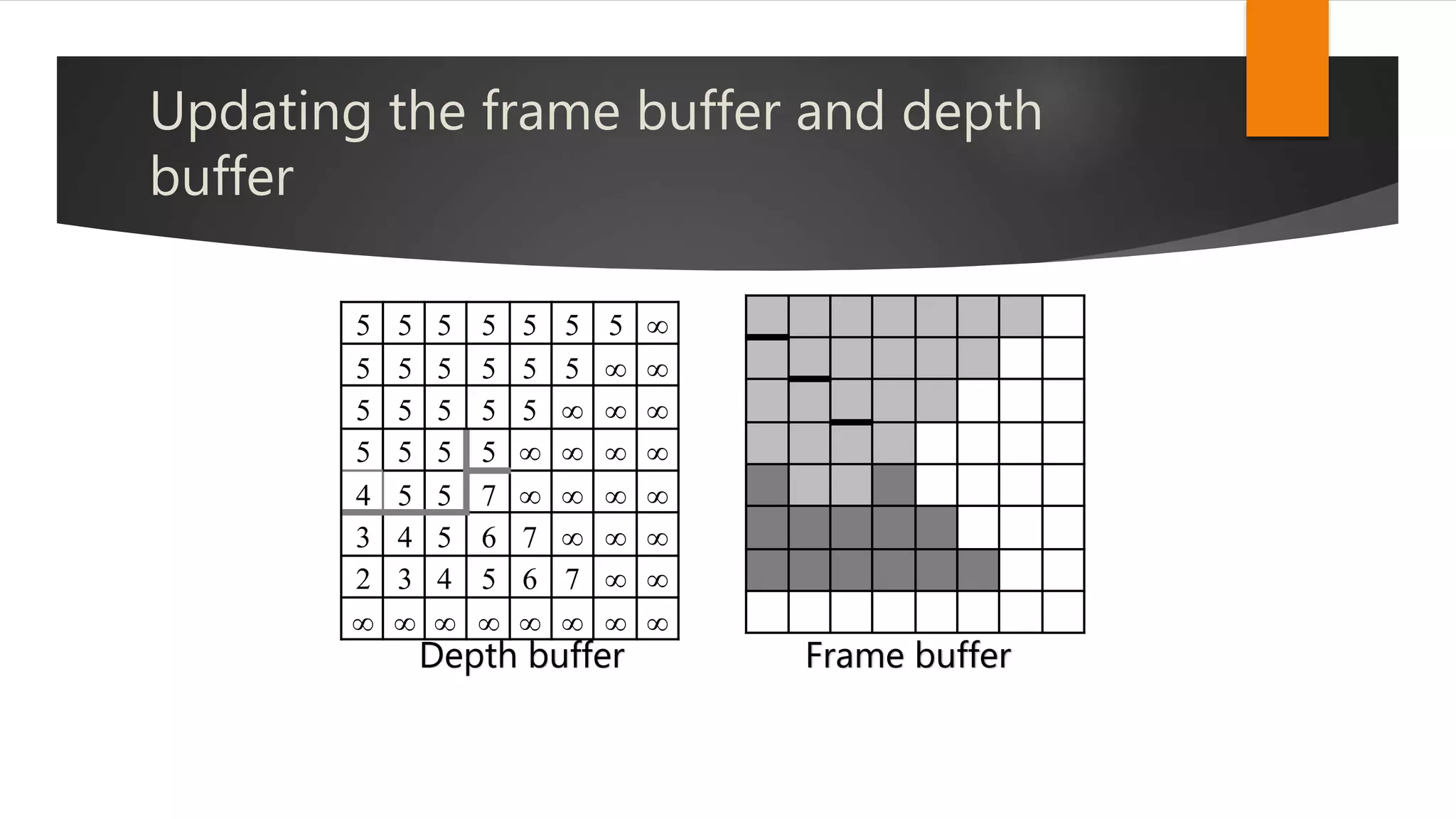
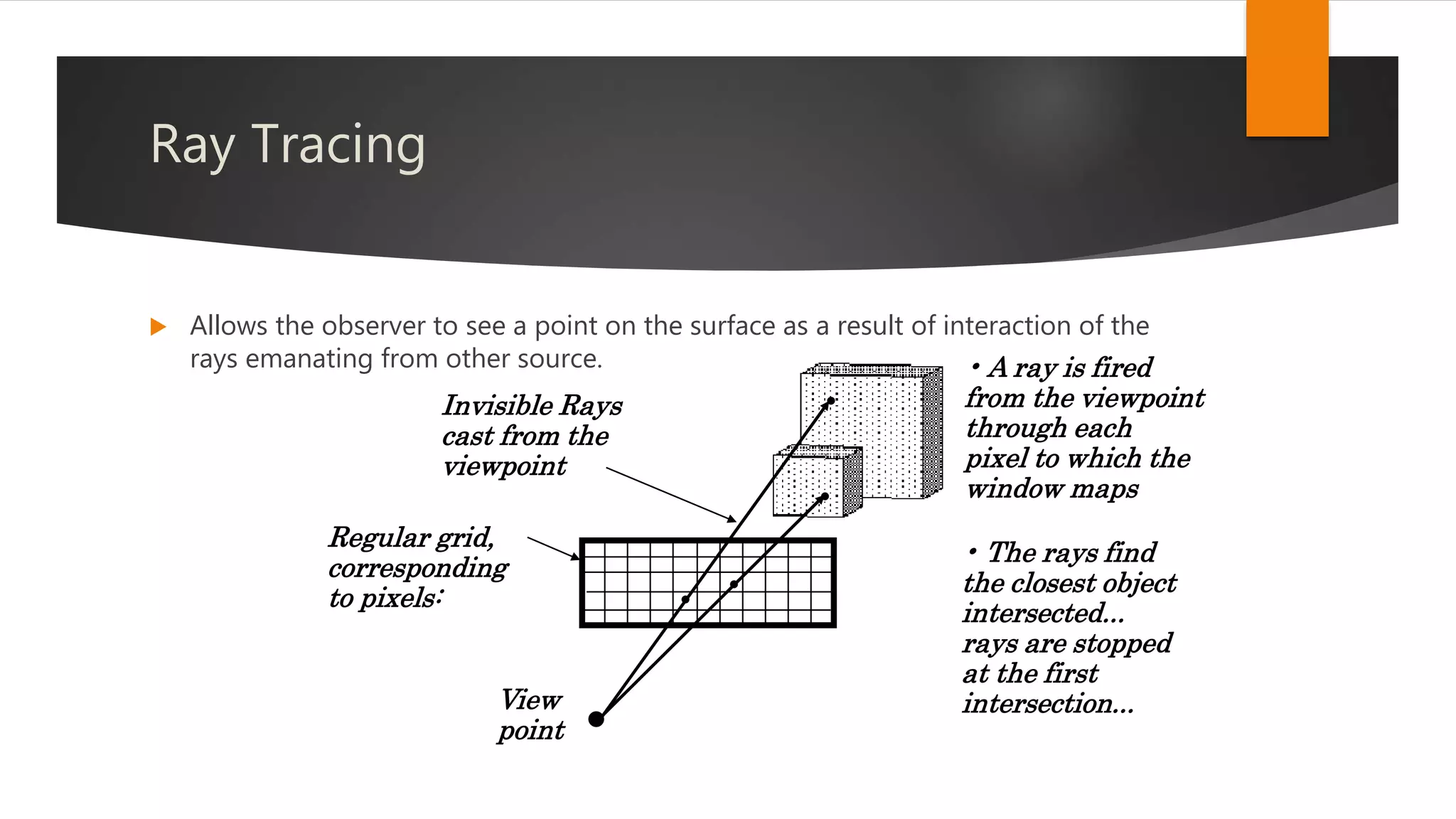
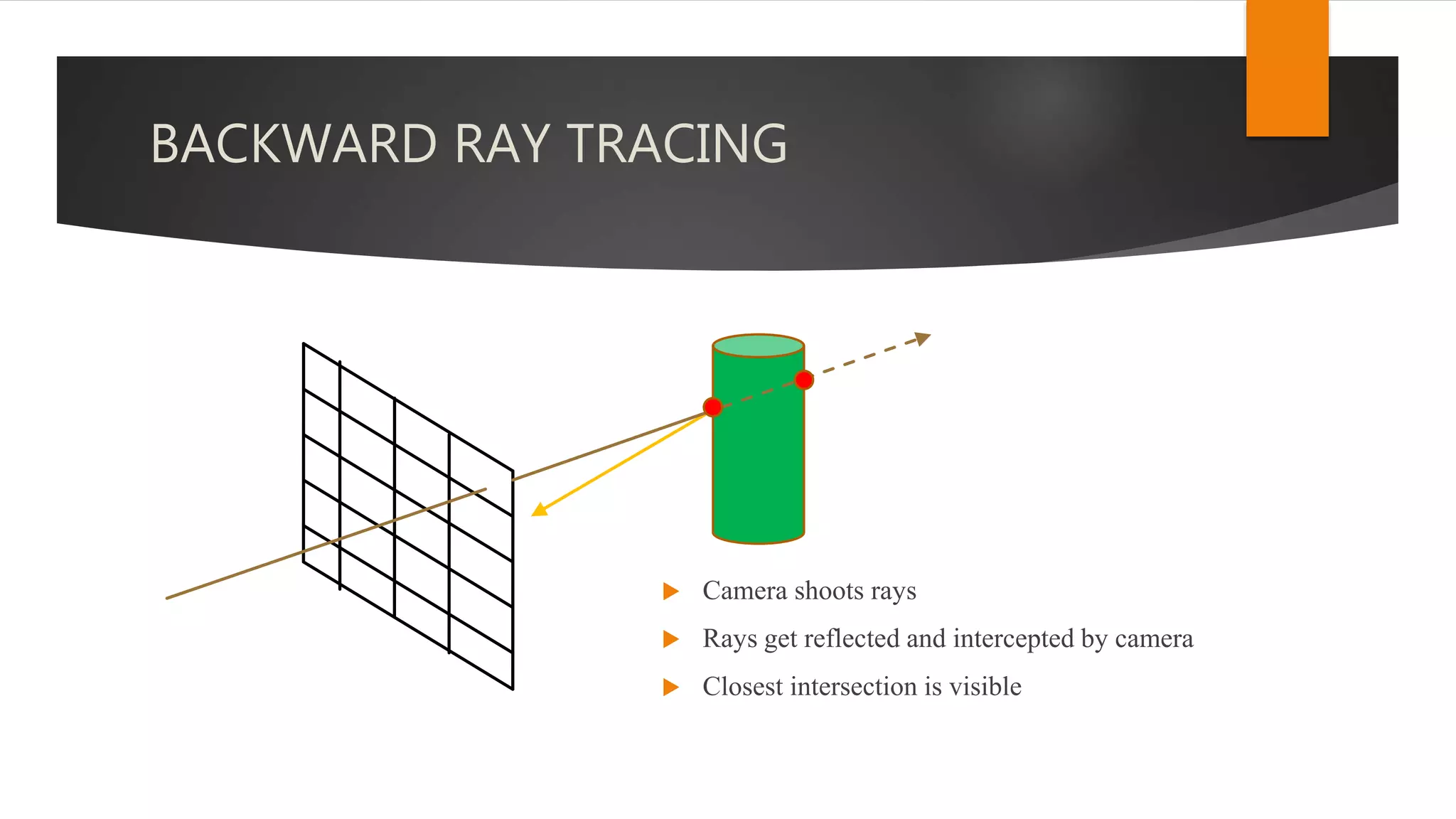
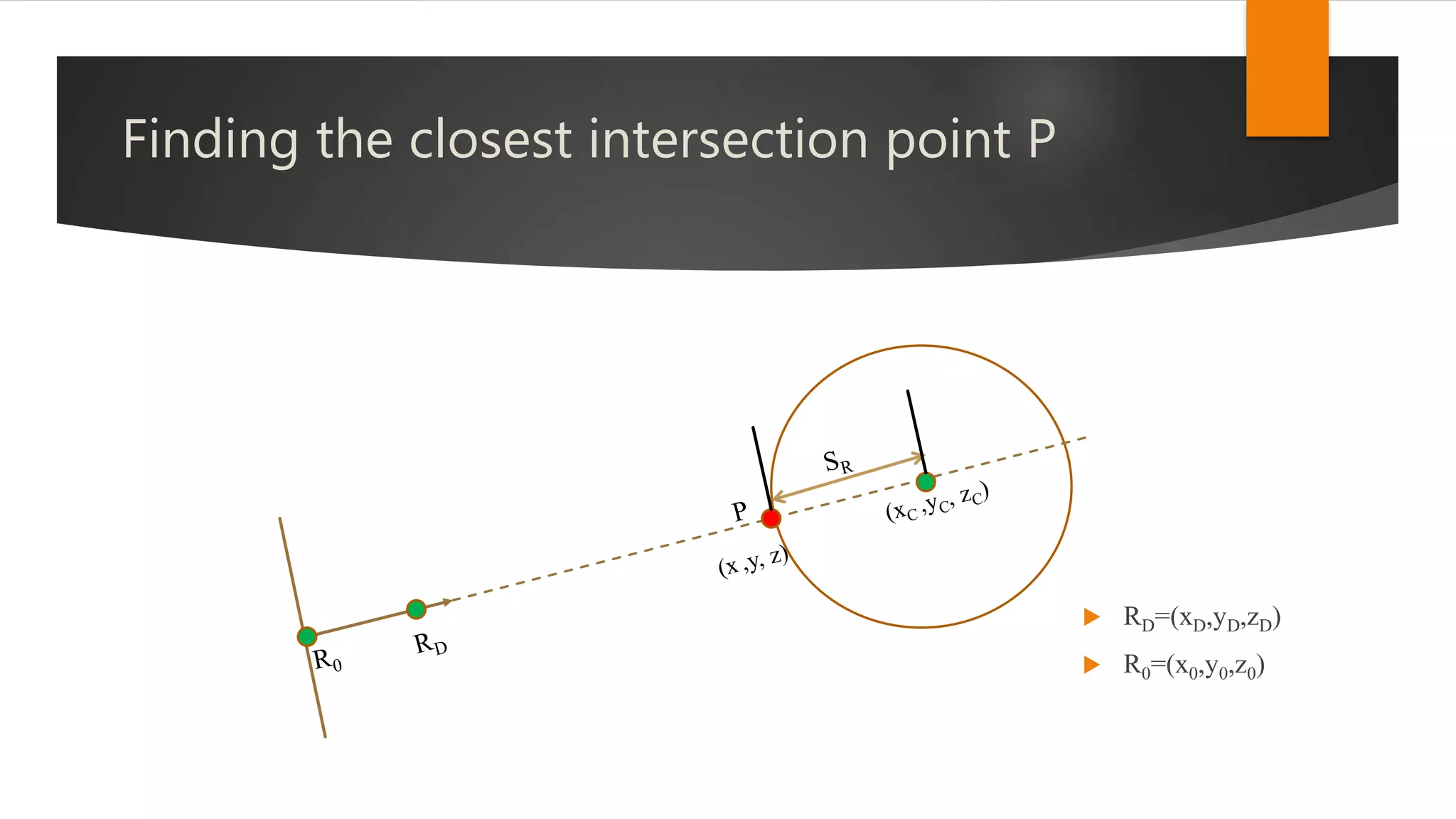
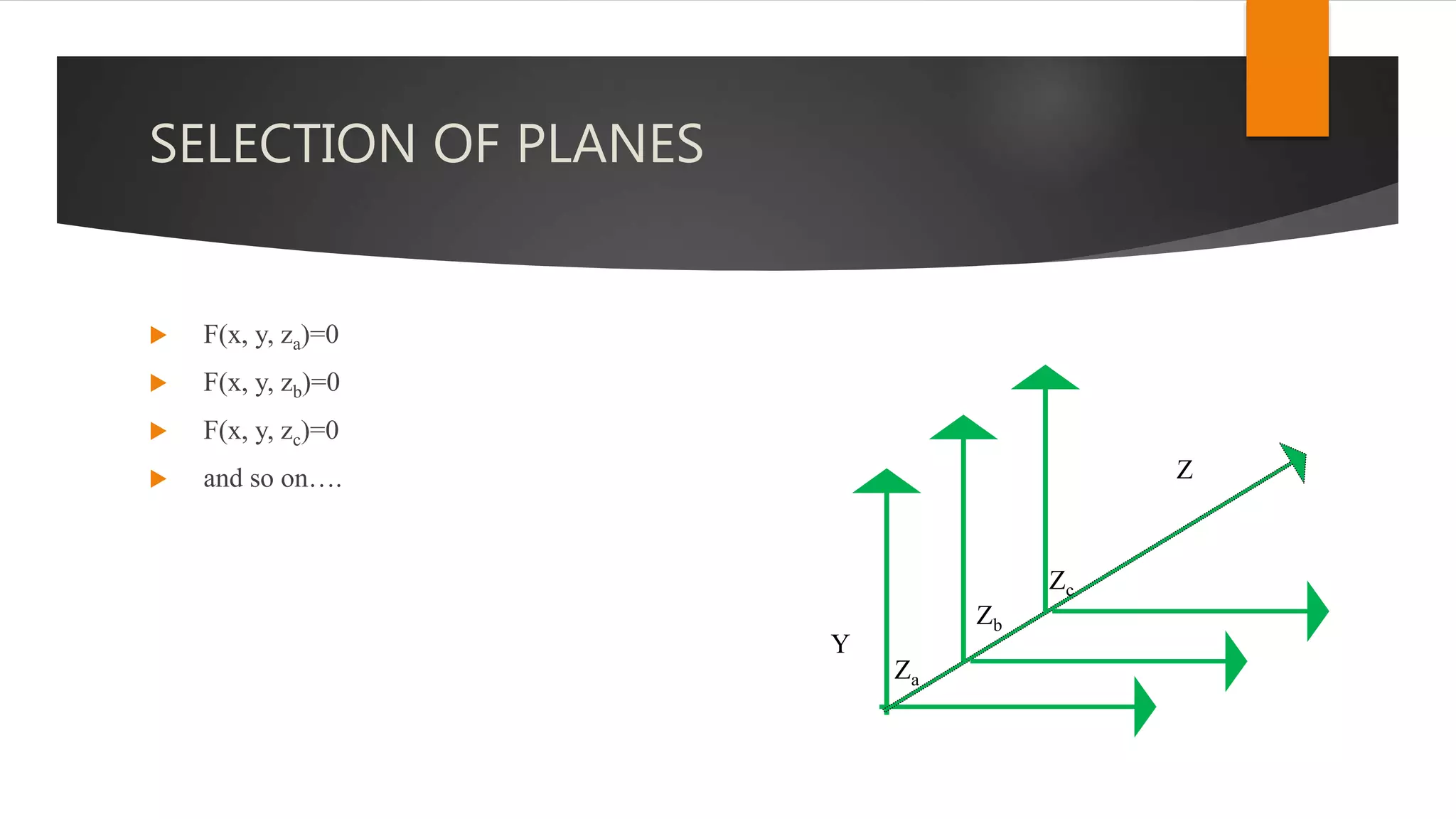
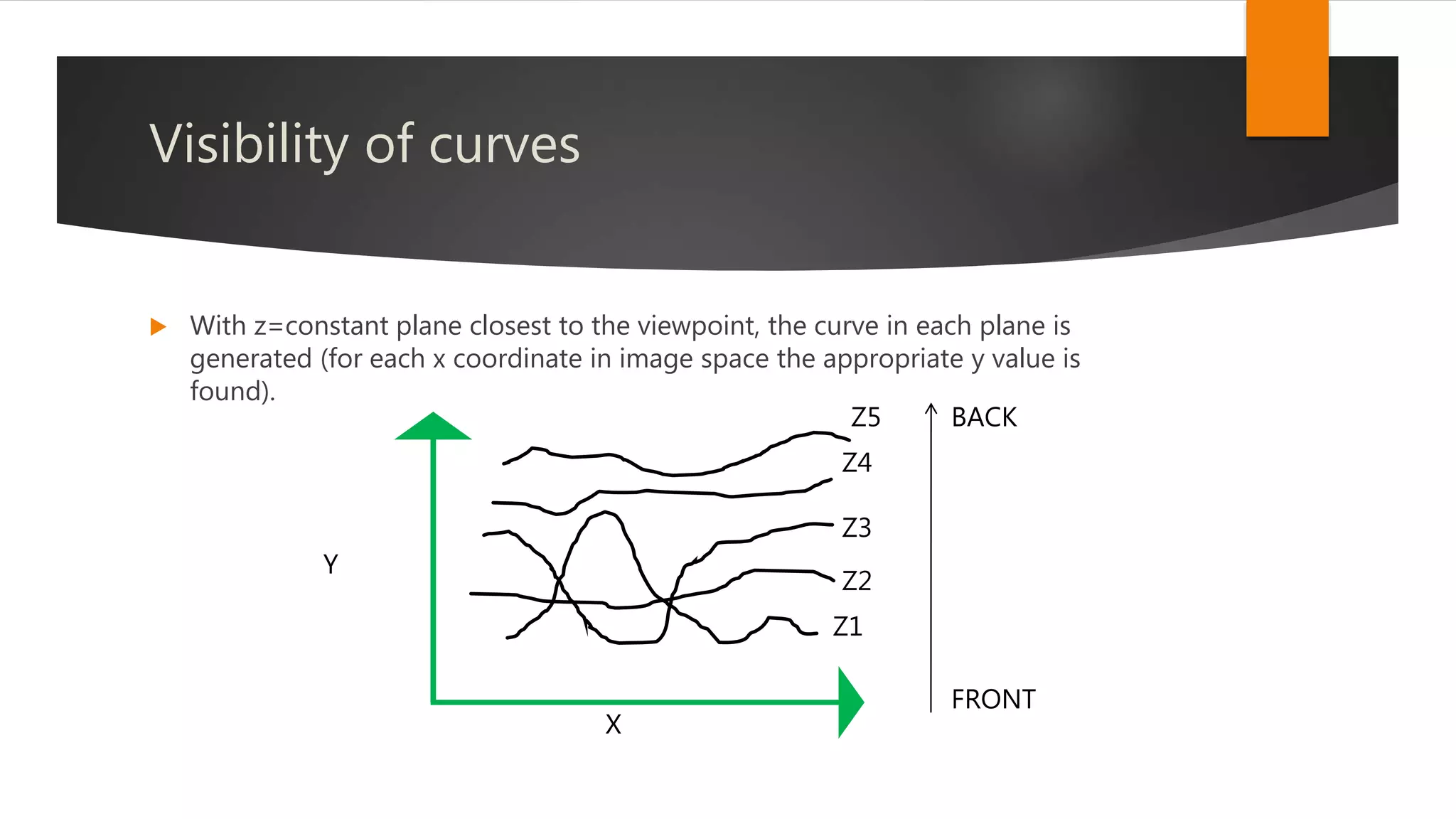
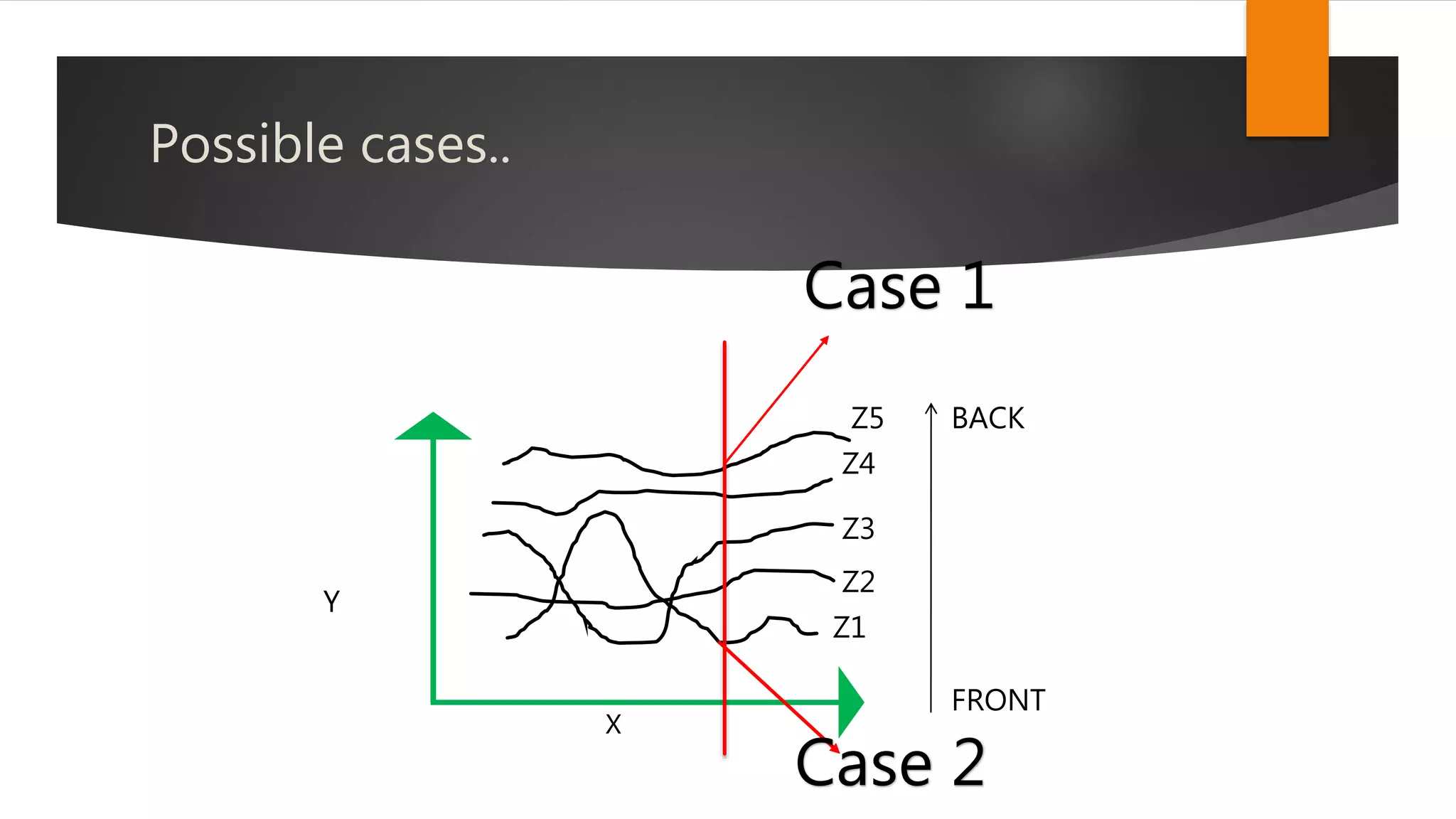
The document discusses hidden surface removal techniques in 3D graphics, emphasizing its necessity for realistic rendering by eliminating spurious surfaces. It outlines two main approaches: object space and image space, detailing algorithms like Roberts, Z-buffer, and ray tracing. Additionally, it describes the mechanics of Z-buffering, ray tracing, and the computational costs associated with different methods.

1. HIDDEN SURFACE REMOVAL
MADE BY
PUNYAJOY SAHA

2. What is a hidden surface?
 When we view a picture containing non-transparent objects and surfaces, then we cannot see
those surfaces from view which are behind from surfaces closer to eye.
Visible surfaceHidden surface

3. Why hidden surface removal is needed?
 If we don’t remove hidden surface, there may be some spurious surfaces in the 3d object.
 We must remove these hidden surfaces to get a realistic screen image.
3D object with false surfaces 3D object with true surfaces
False surface

4. Two types of approaches
 Object space approach
 Image space approach

5. OBJECT SPACE APPROACH
 Algorithm
for(each object in the world)
{
determine those parts of the object whose view is unobstructed
by other parts of it or any other object;
draw those parts in the appropriate colour
}
 Computational cost: O(n^2) (n is number of objects)
 Examples: . Roberts algorithm, Warnock’s algorithm

6. IMAGE SPACE APPROACH
 Algorithm
for(each pixel in the image)
{
determine the object closest to the viewer that is intercepted by
the projector through the pixel;
draw the pixel in the appropriate colour;
}
 Computational cost: O(np) (n:number of object p:number of pixels)
 Examples: . Z-buffer, Floating horizon algorithm

7. Image space approaches
 Floating horizon
 Z-buffer
 Ray tracing

8. Floating Horizon Algorithm
The technique is to convert 3D problem to equivalent 2D problem by intersecting 3D surface
with a series of parallel cutting planes at constant values of the coordinate in the view
direction. It could be x, y or z. The function F(x,y,z)=0 is reduced to a planar curve in each of
these parallel planes
y  f (x,z)

9. SELECTION OF PLANES
 F(x, y, za)=0
 F(x, y, zb)=0
 F(x, y, zc)=0
 and so on….
Y
Z
Za
Zc
Zb

10. Visibility of curves
 With z=constant plane closest to the viewpoint, the curve in each plane is
generated (for each x coordinate in image space the appropriate y value is
found).
X
Y
FRONT
BACK
Z1
Z2
Z3
Z4
Z5

11. Possible cases..
X
Y
FRONT
BACK
Z1
Z2
Z3
Z4
Z5
Case 1
Case 2

12. Z-Buffer Algorithm
 In this process depth of the z-axis is used to determine the closest (visible surface).
 The depth value of a pixel is compared and the closest surface determines the colour
 Depth buffer ( values between 0 to inf) for each pos (x,y).
 Frame buffer is used to store the intensity of the colour value.
Intensity f(x ,y)
Depth Z(x ,y)
INTENSITY DEPTH

13. Pseudo code
 Initialize all d[i,j]=inf (max depth), c[i,j]=background color.
for (each polygon)
{
for (each pixel in polygon’s projection)
{
Find depth-z of polygon at (x,y) corresponding to pixel (i,j);
If z < d[i,j]
{
d[i,j] = z;
p[i,j] = color;
}
}
}

14. X
Y
Z
Za
Zb
Zc
(x,y)
Example
Not parallel to XY
plane
parallel to XY
plane

15. α α α α α α α α
α α α α α α α α
α α α α α α α α
α α α α α α α α
α α α α α α α α
α α α α α α α α
α α α α α α α α
α α α α α α α α
BG BG BG BG BG BG BG BG
BG BG BG BG BG BG BG BG
BG BG BG BG BG BG BG BG
BG BG BG BG BG BG BG BG
BG BG BG BG BG BG BG BG
BG BG BG BG BG BG BG BG
BG BG BG BG BG BG BG BG
BG BG BG BG BG BG BG BG
DEPTH BUFFER
FRAME BUFFER
Initialisation

16. Parallel with
the image plane 
 
      
     
    
   
  
 

Checking the first surface….

17. Updating the frame buffer and depth
buffer
       
       
       
       
       
       
       
       
Depth buffer Frame buffer

18. Checking the second surface….




 
  
   
    
     

19. Updating the frame buffer and depth
buffer
       
       
       
       
       
       
       
       
Depth buffer Frame buffer

20. Ray Tracing
 Allows the observer to see a point on the surface as a result of interaction of the
rays emanating from other source.
•
•
•
View
point
•
•
Invisible Rays
cast from the
viewpoint
Regular grid,
corresponding
to pixels:
• The rays find
the closest object
intersected...
rays are stopped
at the first
intersection...
• A ray is fired
from the viewpoint
through each
pixel to which the
window maps

21. Pseudo code:
For each scan line in the image
For each pixel in a scan line
• Determine the ray from the viewpoint (or center of
projection) through the pixel;
• For each object in the scene
– If the object is intersected and is closest found so
far...then record the intersection and object's name;
• Set the pixel's color to the closest object intersection;

22. BACKWARD RAY TRACING
 Camera shoots rays
 Rays get reflected and intercepted by camera
 Closest intersection is visible

23. Finding the closest intersection point P
 RD=(xD,yD,zD)
 R0=(x0,y0,z0)

24. 2 2 2
D
0 D
D D
t 0
x y z 1
R(t) R R t 
 



2 2 2 2
C C C R(x x ) (y y ) (z z ) S     
Given equations
 Ray equation
We consider the ray towards the scene not opposite to the
scene
We consider normalized direction of the ray i.e. perpendicular to
the viewer’s plane
 Sphere equation

25. Calculations
 Put the ray equation into sphere equation and solve t
 We get:
Find the value of closest t from R0
0 D
0 D
0 D
x x x t
y y y t
z z z t
 
 
 
2 2 2
D D D
D 0 C D 0 C D 0 C
2 2 2
0 C 0 C 0
2
C
A x y z
B (x (x x ) y (y y ) z (z z ))
C (x x ) (y
At Bt C
y ) ( )
0
z z
 
  
     
   

 

26. THANK YOU