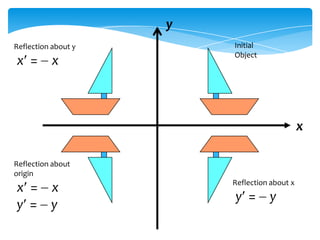
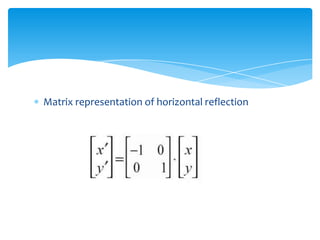
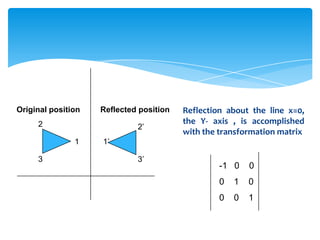
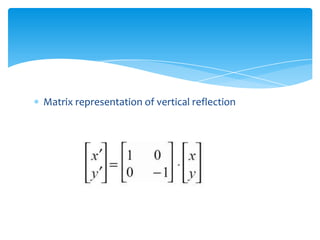
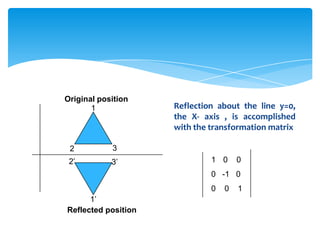
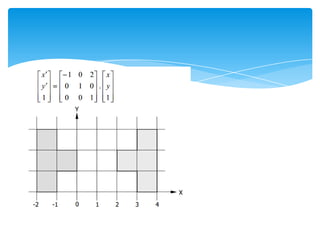
This document discusses reflections in 2-D spaces. It defines reflection as rotating an object 180 degrees around a reflection axis. It shows examples of reflecting objects about the y-axis and x-axis, as well as the transformation matrices used for horizontal and vertical reflections. It also provides an example of reflecting about a non-standard axis, in this case the line x=1, and shows the steps and resulting transformation.

1. Reflection in 2-D
By: Tripti Saxena

2. Reflection is a transformation that produces a mirror
image of an object. It is obtained by rotating the
object by 180 degree about the reflection axis

3. y
Reflection about y
x = x
Initial
Object
x
Reflection about
origin
x = x
y = y
Reflection about x
y = y

4. Matrix representation of horizontal reflection

5. Original position
Reflected position
2
2’
1
3
Reflection about the line x=0,
the Y- axis , is accomplished
with the transformation matrix
1’
3’
-1 0
0
0
1
0
0
0
1

6. Matrix representation of vertical reflection

7. Original position
1
2
3
2’
3’
Reflection about the line y=0,
the X- axis , is accomplished
with the transformation matrix
1 0
0
0 -1 0
0
1’
Reflected position
0
1

8. Example
Example: To make a reflection about the vertical axis x = 1.
Steps:
Subtract 1 from the x-coordinate.
This effectively makes the x = 1 axis coincident with the major
y axis.
Perform the reflection by reversing the sign of the modified x
coordinate.
Add 1 to the reflected coordinate to compensate for the
original subtraction.

9. x1 = x −1
x2 = −(x − )1
x
′ = −(x −1) +1
which simplifies to
x
′ = −x + 2
y
′=y

10. x
′ = −x + 2
y
′=y
or in matrix form