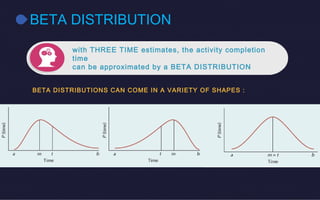
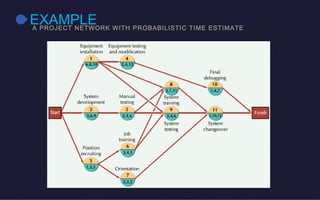
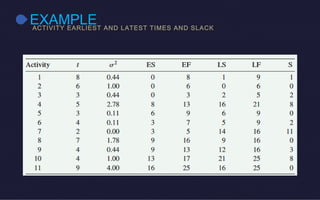
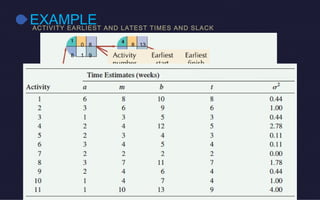
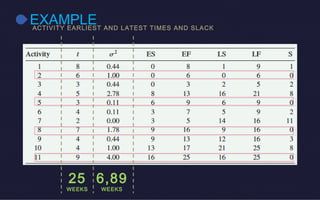
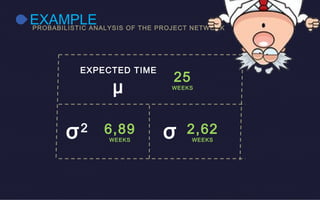
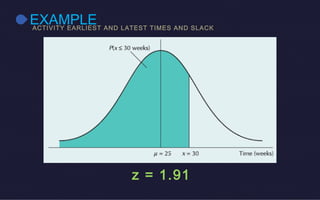
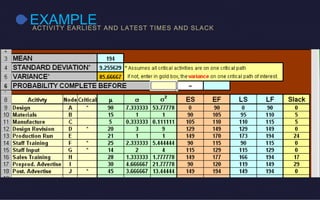
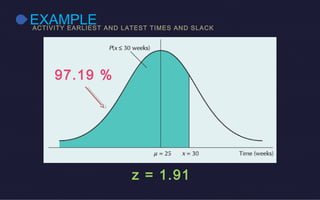
This document discusses probabilistic activity times in project management. It explains that probabilistic estimates allow for variation by using three time estimates - optimistic, most likely, and pessimistic - for each activity. These estimates are used to model the activity times with a beta distribution defined by a mean and variance. An example project network is presented that calculates earliest and latest times, slack, and performs probabilistic analysis to determine the likelihood of completing within a proposed time.

1. Probabilistic Activity Times
Probabilistic Time Estimates
Carrine Kezia Aulia :: 102183022

2. • Single time estimates
• Didn’t allow for any variation
• AT treated as if they are known for
certain
COMPARISON CPM AND
PERTREVIEW
• Multiple time estimates
• Allow for any variation
• AT treated as probabilistic
PERT uses probabilistic activity times
CPM PERT

3. Approach to estimating activity times
WHAT IS PROBABILISTIC ACTIVITY
TIMES?What’s it all about?
• Completion time estimates can be estimated using the
Three Time EstimateThree Time Estimate approachapproach
• In this approach, three time estimates are required for each activity

4. MOST LIKELY TIME (m)
THREE TIME ESTIMATES
OPTIMISTIC TIME (a)
PESSIMISTIC TIME (b)
1
2
3
most frequently occur if the activity were
repeated many times
the shortest possible time to complete the
activity if everything went right
the longest possible time to complete the
activity if everything went wrong

5. with THREE TIME estimates, the activity completion
time
can be approximated by a BETA DISTRIBUTION
BETA DISTRIBUTION
BETA DISTRIBUTIONS CAN COME IN A VARIETY OF SHAPES :

6. FORMULA
MEAN AND VARIANCE
a + 4m + b
6
b - a
6
2
mean (expected time)
variance σ2
t
MOST LIKELY TIME (m)
OPTIMISTIC TIME (a)
PESSIMISTIC TIME (b)

7. EXAMPLEA PROJECT NETWORK WITH PROBABILISTIC TIME ESTIMATE

8. EXAMPLEACTIVITY TIME ESTIMATES
a + 4m + b
6
b - a
6
2
t σ2

9. EXAMPLEACTIVITY EARLIEST AND LATEST TIMES AND SLACK

10. EXAMPLEACTIVITY EARLIEST AND LATEST TIMES AND SLACK
0
8
8 8
5
13
0
6
6
3
0 3
3
6 9
4
3 7
2
3 5
7
9 16
4
9 13
4
13 17
9
16 25
2516
2521
2116
169
1612
1614
95
52
9660
91
EXPECTED TIME : 25
CRITICAL PATH :
2-5-8-11

11. EXAMPLEACTIVITY EARLIEST AND LATEST TIMES AND SLACK
25
WEEKS
6,89
WEEKS

12. EXAMPLEPROBABILISTIC ANALYSIS OF THE PROJECT NETWORK
ADD ALL THE σ2
OFF THE CRITICAL
PATH
S
D
what does this formula means?
what does these numbers mean?

13. EXAMPLEPROBABILISTIC ANALYSIS OF THE PROJECT NETWORK
25
WEEKS
6,89
WEEKS
2,62
WEEKS
EXPECTED TIME
μ
σ2
σ

14. EXAMPLEPROBABILISTIC ANALYSIS OF THE PROJECT NETWORK
25
WEEKS
EXPECTED TIME
μ
30
WEEKS
PROPOSED PROJECT TIME
X WHAT IS THE
PROBABILITY THAT
THE SYSTEM WILL BE
READY BY THAT
TIME?
WHAT IS THE
PROBABILITY THAT
THE SYSTEM WILL BE
READY BY THAT
TIME?

15. EXAMPLEPROBABILISTIC ANALYSIS OF THE PROJECT NETWORK
Z =
X – μ
σ
30
WEEKS
25
WEEKS
2.62
-
= 1.911.91

16. EXAMPLEACTIVITY EARLIEST AND LATEST TIMES AND SLACK
z = 1.91

17. EXAMPLEACTIVITY EARLIEST AND LATEST TIMES AND SLACK

18. EXAMPLEACTIVITY EARLIEST AND LATEST TIMES AND SLACK
0.9719
probability of completing
the project in 30 days
0.9719
probability of completing
the project in 30 days

19. EXAMPLEACTIVITY EARLIEST AND LATEST TIMES AND SLACK
www.measuringusability.com

20. EXAMPLEACTIVITY EARLIEST AND LATEST TIMES AND SLACK
z = 1.91
97.19 %