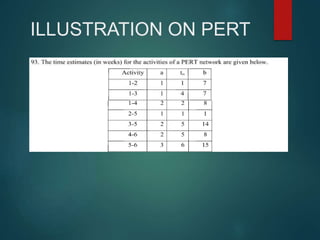
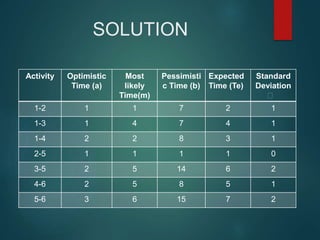
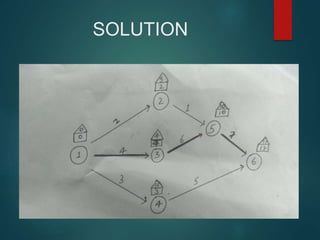
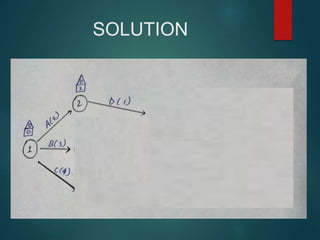
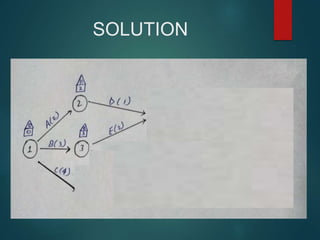
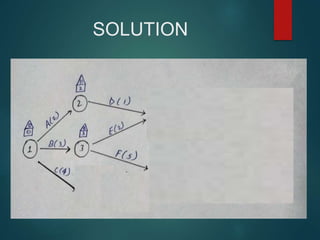
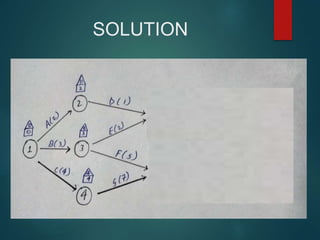
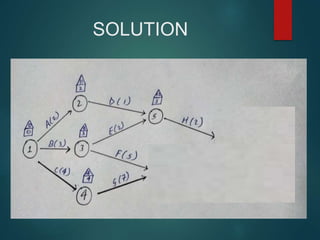
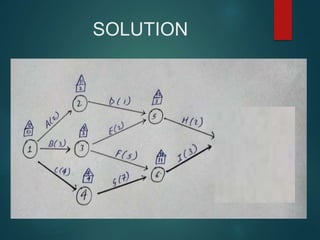
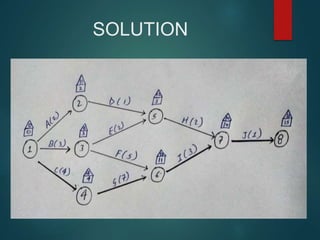
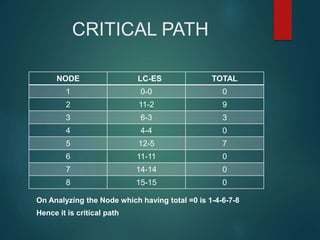
PERT and CPM are techniques used in project network analysis for planning, management, and control of projects. PERT uses probabilistic time estimates and is used for non-repetitive projects with uncertain timelines, while CPM uses deterministic single estimates and is used for repetitive jobs with past experience to predict times. Both techniques involve modeling the project as a network of activities and events, identifying the critical path of zero slack activities that dictates the minimum project duration.

1. PERT & CPM
SUBMITTED BY:-
SHASHANK KAPOOR
MECHANICAL , 154169

2. What isthe PERT&CPM?
It is nothing but the technique used in Network analysis
of project management, such as planning ,
management and control of project.
So, what is project ??
“A project is a series of activities directed
to accomplishment of a desired objective.”
Plan your work first…..then work your plan

3. Project Evaluation & Review
Techniques
(PERT)
In PERT is basicallyamethod to analyze the tasks involved in
completing agiven project,especially the time neededto completeeachtask,
and to identify the minimum time neededto complete the total project.
– Multiple time estimates
– Probabilistic activity times
USED IN : Project management - for non-repetitive jobs
(research and development work), where the time and cost
estimates tend to be quite uncertain. This technique uses
probabilistic time estimates.

4. Critical Path Method
(CPM)
In CPM activities are shown as a network of
precedence relationships using activity-on-node network
construction.
– Single estimate of activity time
– Deterministic activity times
USED IN : Production management - for the jobs of
repetitive in nature where the activity time
estimates can be predicted with considerable
certainty due to the existence of past experience.

5. KEY ELEMENTS
 Arrows:- leading from tail to head directionally Indicate
Activity
 Nodes:- Indicate Event, a point in time where one or more activities start
and/or finish.
 Earliest time:It is categorized in two sub elements.
1. Earliest Starting time (ES):-Time at which the activity can
start
2. Earliest finishing time(EF):-Equals to the earliest start time
for the activity plus the time required to complete the
activity
 Latest time :It is categorized in two sub elements.
1.Latest Starting time (LS):-Time in which the activity can be
completed without delaying
2.Latest Finishing time (LF):-equal to the latest finish time minus the time
required to complete the activity.
 Slack time:-The difference between its earliest and latest start time.
 Critical Path:-The path of activities having zero Slack time.

6. KEY ELEMENTS
 Optimistic time (a): – It is the shortest time in which the activity
can be completed.
 Most likely time (m) – It is the probable time required to perform
the activity.
 Pessimistic time (b)– It is the longest estimated time required to
perform an activity .
 Expected time (Te) – approximation time taken to complete an
activity.
Te=
𝒂+𝟒𝒎+𝒃
𝟔
 Standard deviation ( ) – Higher the SD is the greater amount of
uncertainty exists
 Variance (𝝈 𝟐
) − Large variance indicates great uncertainty, a small
variance indicates a more accurate estimate
=
𝑏−𝑎
6

7. ILLUSTRATION ON PERT

8. SOLUTION
Activity Optimistic
Time (a)
Most
likely
Time(m)
Pessimisti
c Time (b)
Expected
Time (Te)
Standard
Deviation
1-2 1 1 7 2 1
1-3 1 4 7 4 1
1-4 2 2 8 3 1
2-5 1 1 1 1 0
3-5 2 5 14 6 2
4-6 2 5 8 5 1
5-6 3 6 15 7 2

9. SOLUTION

10. CRITICAL PATH
 Paths:-
1-2-5-6 = 2+1+7=10
1-3-5-6 = 4+6+7=17
1-4-6 = 3+5=8
 1-3-5-6 is critical path since it take maximum time.

11. CRITICAL PATH
NODE LC-ES TOTAL
1 0-0 0
2 9-2 7
3 4-4 0
4 12-3 9
5 10-10 0
6 17-17 0
On Analyzing the Node which having total =0 is 1-3-5-6
Hence it is critical path

12. PROBABILISTIC
DETERMINATION
 What isthe Probability of it taking20 weeks?
CriticalPath=1-3-5-6=17weeks
T =20 weeks C=17 weeks
𝑧 = 𝑇−𝐶
𝜎2
(Variance) 𝜎2 = 1 + 4 + 4 = 9
𝑧 = 20−17
9
= 1
Lookup Zvalue in normal distribution table
Pz=0.8413 or 84.13%
Goingover 20 weeks would be 100 – 84.13 = 15.87%
(Probability of ittaking 20 weeks)

13. ILLUSTRATION ON CPM

14. SOLUTION

15. SOLUTION

16. SOLUTION

17. SOLUTION

18. SOLUTION

19. SOLUTION

20. SOLUTION

21. SOLUTION

22. SOLUTION

23. SOLUTION

24. SOLUTION

25. CRITICAL PATH
 Paths:-
 1-2-5-7-8=2+1+2+1=6 days
 1-3-5-7-8=3+2+2+1=8 days
 1-3-6-7-8=3+5+3+1=12days
 1-4-6-7-8=4+7+3+1=15 days
1-4-6-7-8 is critical path since it take maximum
time.

26. CRITICAL PATH
NODE LC-ES TOTAL
1 0-0 0
2 11-2 9
3 6-3 3
4 4-4 0
5 12-5 7
6 11-11 0
7 14-14 0
8 15-15 0
On Analyzing the Node which having total =0 is 1-4-6-7-8
Hence it is critical path

27. What happen if we have large
number of Network problem??

28. Conclusion
 For large number of network problem Ford
Fulkerson Max Flow Algorithm is the point
that can give us the optimal critical path
since it is use for finding the maximum flow
in a flow network for single source and single
sink.

29. THANK YOU