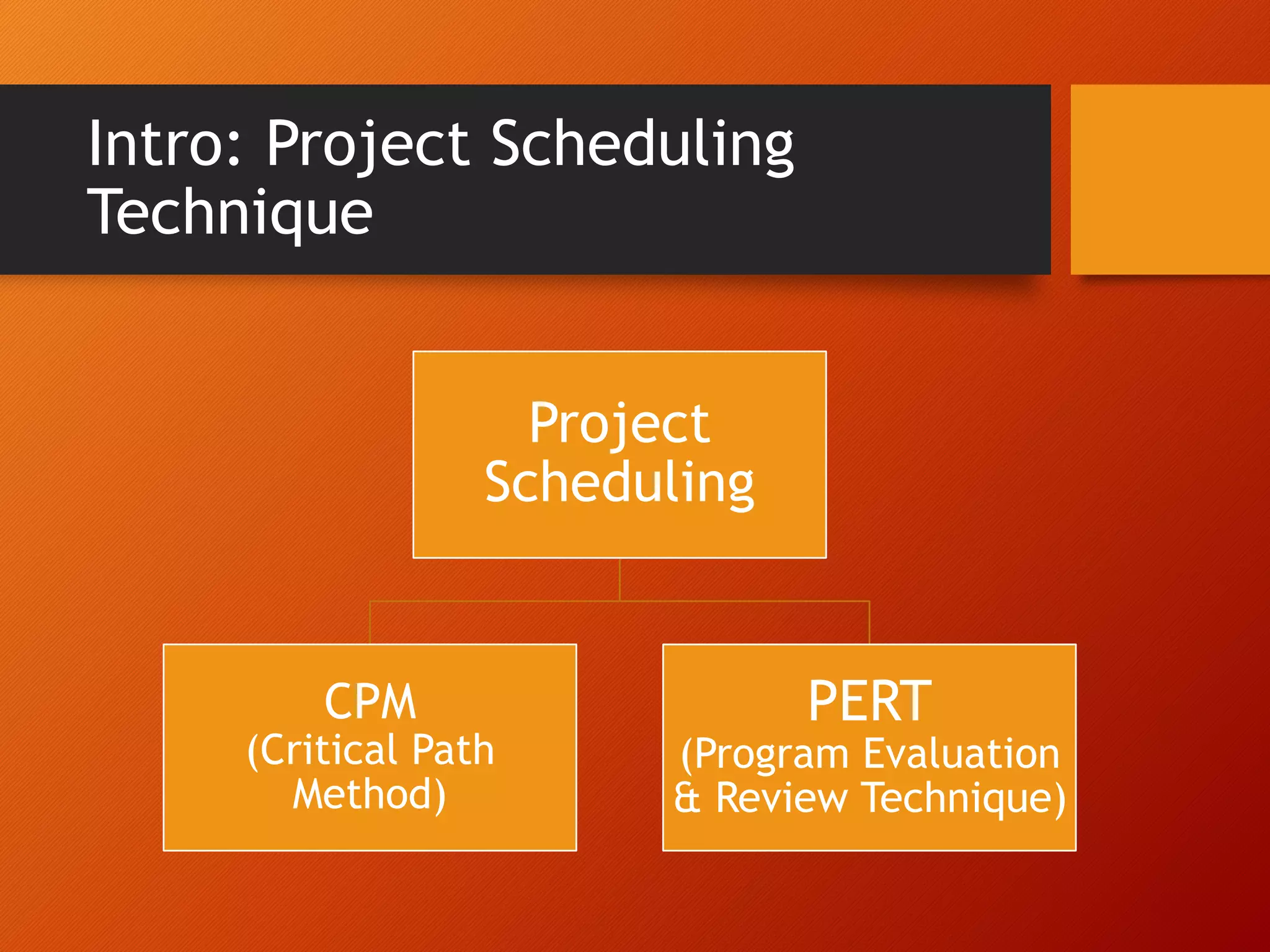
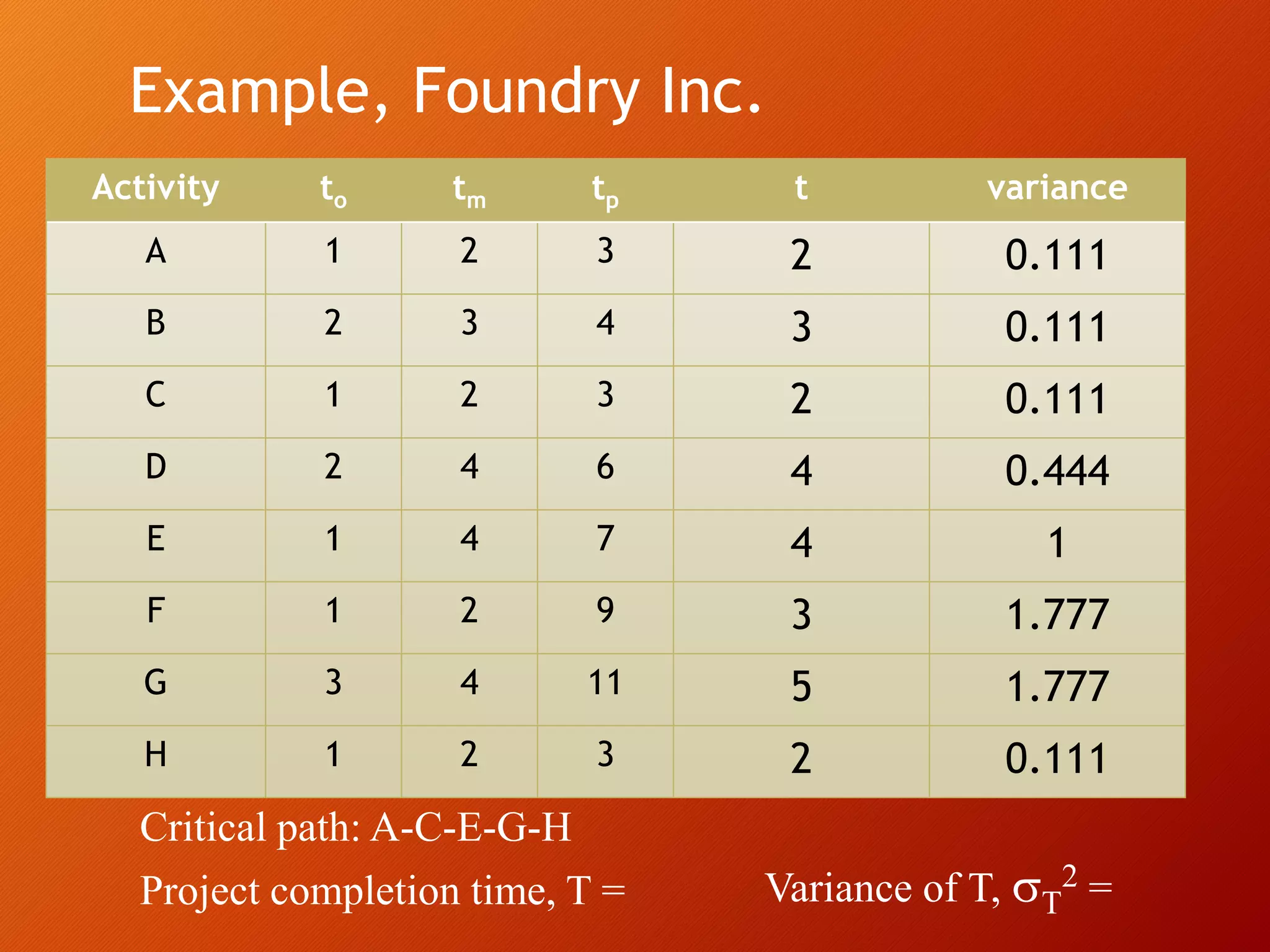
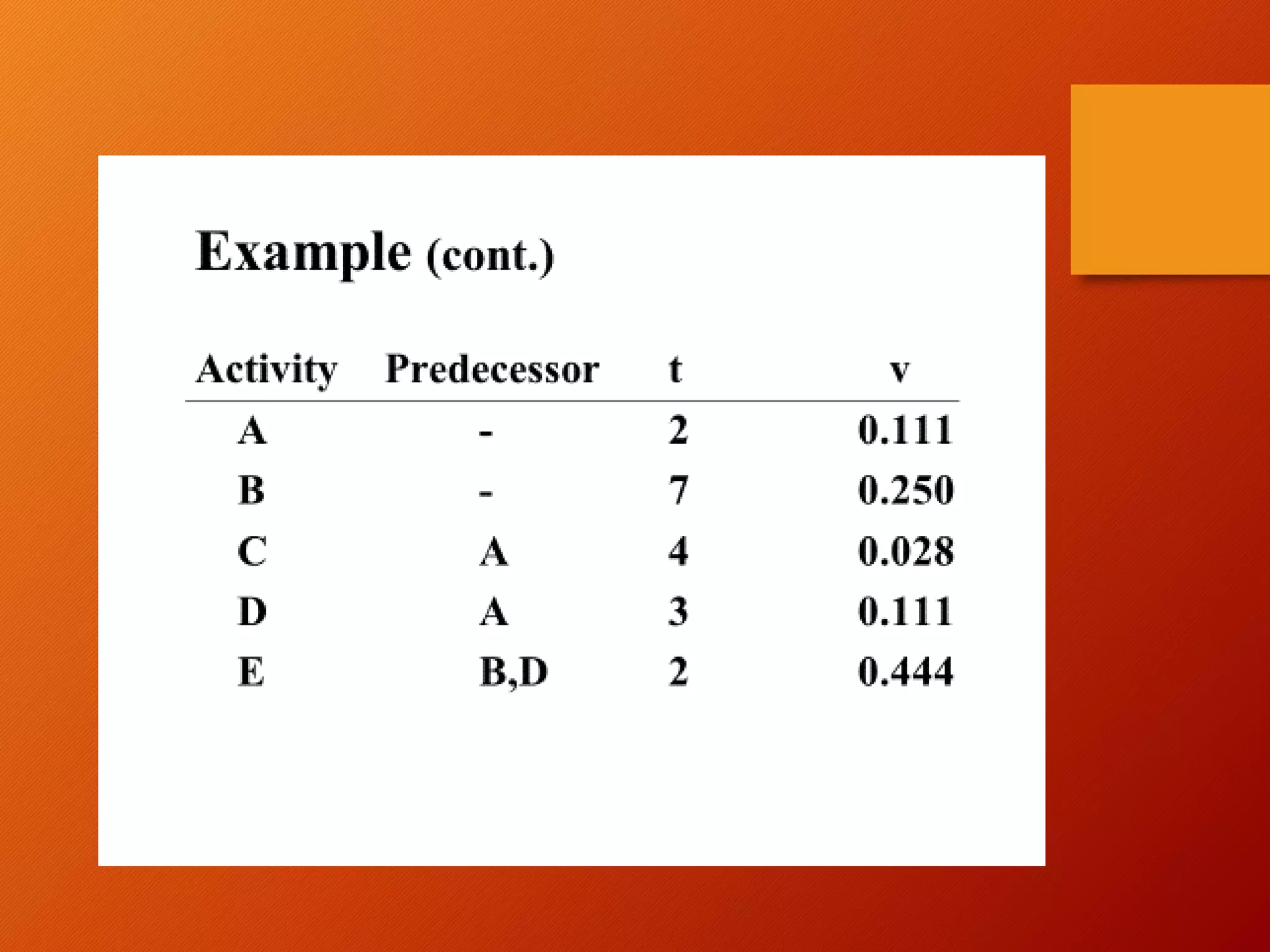
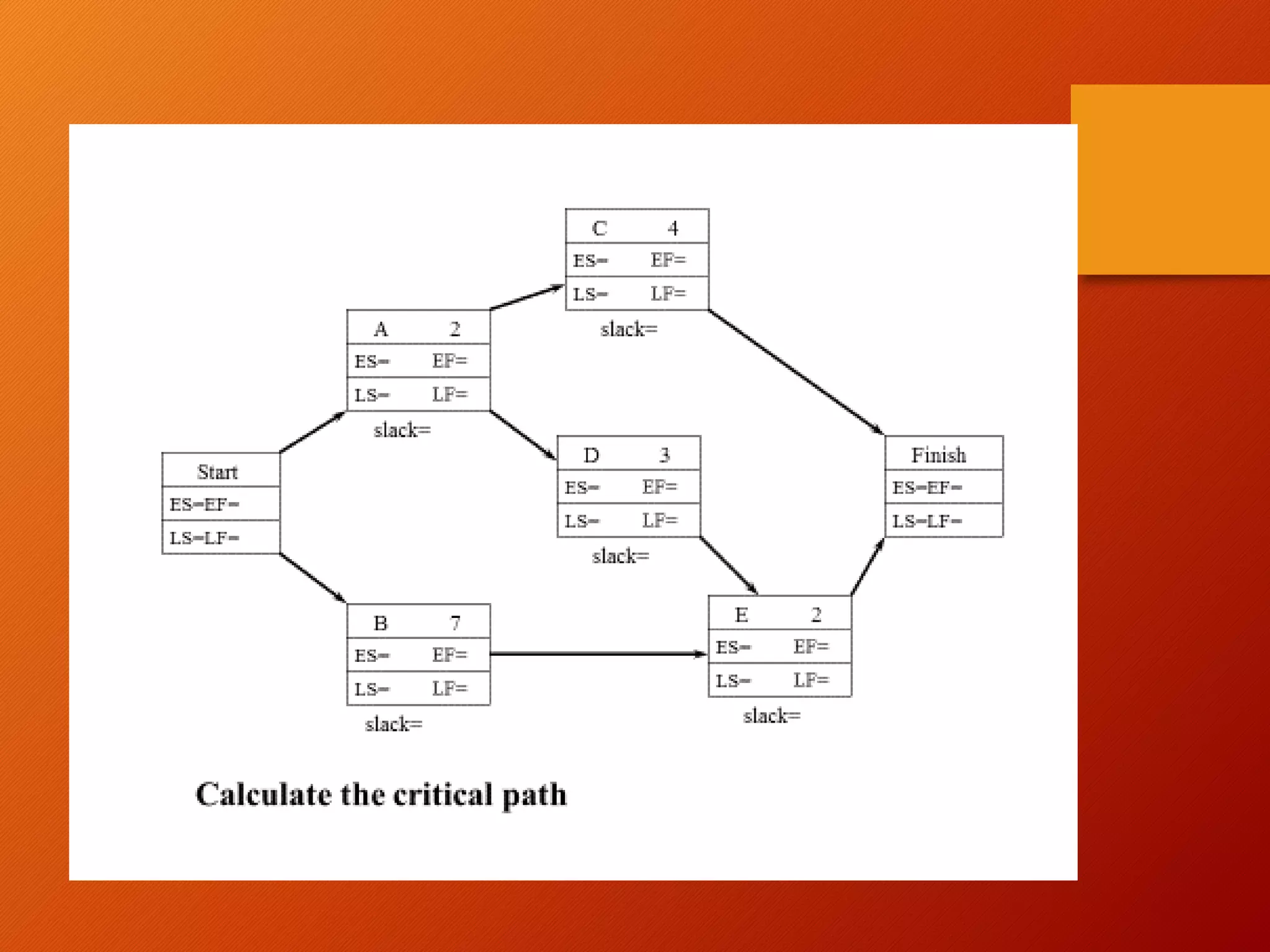
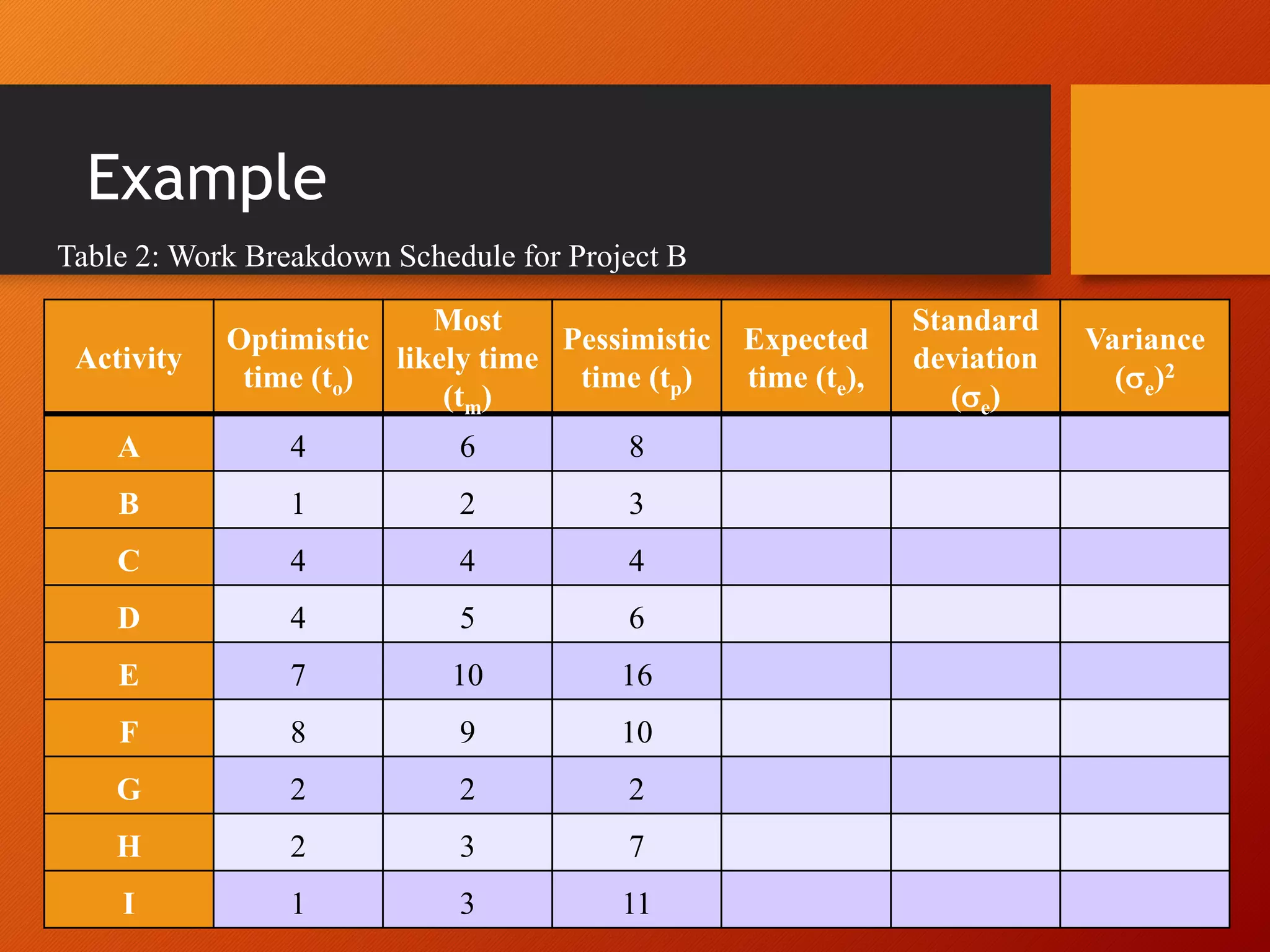
This document discusses project scheduling techniques CPM (Critical Path Method) and PERT (Program Evaluation and Review Technique). It defines CPM and PERT, compares their key differences, and provides examples of how to apply them. Specifically, it covers how to calculate activity times and variances in PERT, identify critical paths, calculate project completion times and probabilities, and perform crashing in CPM. The document aims to help the reader understand how to distinguish and apply CPM and PERT for project scheduling, time and cost analysis, and probability calculations.

1. CPM & PERT
Project Scheduling
FIB36103
Project Management

2. Lesson Outcomes
Distinguish the
difference
between CPM &
PERT
Apply the CPM
Crashing
Technique
Calculate the
PERT time
expected
Determine the
probability of
project
completion time
At the end of this topic, you should be able to:

3. Intro: Project Scheduling
Technique
Project
Scheduling
CPM
(Critical Path
Method)
PERT
(Program Evaluation
& Review Technique)

4. Why PERT/CPM?
• Prediction of deliverables
• Planning resource requirements
• Controlling resource allocation
• Internal program review
• External program review
• Performance evaluation
• Uniform wide acceptance

5. PERT/CPM is supposed to
answer questions such as:
• How long does the project take?
• What are the bottle-neck tasks of the
project?
• What is the time for a task ready to start?
• What is the probability that the project is
finished by some date?
• How additional resources are allocated
among the tasks?

6. Differences: CPM and PERT
CPM
• CPM uses activity oriented network.
(AON)
• Durations of activity may be
estimated with a fair degree of
accuracy.
• It is used extensively in construction
projects.
• Deterministic concept is used.
• CPM can control both time and cost
when planning.
• Cost optimization is given prime
importance. The time for the
completion of the project depends
upon cost optimization. The cost is
not directly proportioned to time.
Thus, cost is the controlling factor.
PERT
• PERT uses event oriented Network.
(AOA)
• Estimate of time for activities are
not so accurate and definite.
• It is used mostly in research and
development projects, particularly
projects of non-repetitive nature.
• Probabilistic model concept is used.
• PERT is basically a tool for planning.
• In PERT, it is assumed that cost varies
directly with time. Attention is
therefore given to minimize the time
so that minimum cost results. Thus in
PERT, time is the controlling factor.

7. CPM Crashing

8. Problem: Crashing
Activity Precedence Duration, Periods
(normal, crash)
Cost
(normal, crash)
Slope
(Cost / Period)
A
B
C
D
E
F
G
-
A
A
A
B
C,D
E,F
4,3
6,4
10,9
11,7
8,6
5,4
4,4
RM 30,40
RM 40,80
RM 30, 45
RM 25, 75
RM 50, 80
RM 20, 35
RM 40,40
10/-1 = - 10
40/-2 = - 20
15/-1 = - 15
50/-4 = - 12.5
30/-2 = - 15
15/-1 = - 15
-
Table 1: CPM (Normal & Crash, duration in day)
a) Reduce the total project duration by three (3) days.
b) Calculate the total new cost of the project?

9. Solution steps: Crashing
1. Develop AON complete with duration and
cost.
2. Determine critical activity.
3. Crashing rules: Crash the critical activity
with the lowest cost by a day.
4. Repeat step 2 and 3.

10. PERT - Probability Duration

11. PERT Network:
• It is a directed network.
• Each activity is represented by a node.
• An arc from task X to task Y if task Y follows
task X.
• A ‘start’ node and a ‘finish’ node are added to
show project start and project finish.
• Every node must have at least one out-going
arc except the ‘finish’ node.

12. Performance Time t of an
Activity
• t is calculated as follows:
where
• to = optimistic time,
• tp = pessimistic time,
• tm = most likely time.
• Note: t is also called the expected performance
time of an activity.
6
)
*
4
( p
m
o t
t
t
t




13. Variance of Activity Time t
• If to, tm, and tp are given for the optimistic, most
likely, and pessimistic estimations of activity k,
variance k2 is calculated by the formula
2
2
6
)
( 






 

o
p
k
t
t
Variance 
𝑆𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝐷𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 𝜎 =
𝑡𝑝 − 𝑡𝑜
6

14. Variance, a Measure of Variation
• Variance is a measure of variation of possible
values around the expected value.
• The larger the variance, the more spread-out
the random values.
• The square root of variance is called standard
deviation.

15. Problem: Calculate the Critical
Path
Activity to tm tp Immediate predecessor
A 1 2 3 -
B 2 3 4 -
C 4 5 6 A
D 8 9 10 B
E 2 5 8 C, D
F 4 5 6 B
G 1 2 3 E

16. Steps for Solving 13-1&2
1. Calculate activity performance time t for
each activity;
2. Draw the PERT network;
3. Calculate ES, EF, LS, LF and slack of each
activity on PERT network;
4. Identify the critical path.

17. Probabilities in PERT
• Since the performance time t of an activity is
from estimations, its actual performance time
may deviate from t;
• And the actual project completion time may
vary.

18. Probabilistic Information for
Management
• The expected project finish time and the
variance of project finish time;
• Probability the project is finished by a certain
date.

19. Project Completion Time and its
Variance
• The expected project completion time T:
• T = earliest completion time of the project.
• The variance of T, T2 :
• T2 = (variances of activities on the critical path)

20. Example, Foundry Inc.
Activity to tm tp t variance
A 1 2 3 2 0.111
B 2 3 4 3 0.111
C 1 2 3 2 0.111
D 2 4 6 4 0.444
E 1 4 7 4 1
F 1 2 9 3 1.777
G 3 4 11 5 1.777
H 1 2 3 2 0.111
Critical path: A-C-E-G-H
Project completion time, T = Variance of T, T
2 =

21. Probability Analysis
• To find probability of completing project
within a particular time x:
• 1. Find the critical path, expected project
completion time T and its variance T2 .
• 3. Find probability from a normal distribution table.
2

T
x
Z
Calculate



23. The Idea of the Approach
• The table gives the probability P(z<=Z) where
z is a random variable with standard normal
distribution, i.e. zN(0,1); Z is a specific
value.
• P(project finishes within x days)
)
(
2
Z
z
P
T
x
z
P
T

















24. Notes (1)
• P(project is finished within x days)
= P(z<=Z)
• P(project is not finished within x days)
= 1P(project finishes within x days)
= 1P(z<=Z)

25. Notes (2)
• If x<T, then Z is a negative number.
• But the table is only for positive Z values.
• For example, Z= 1.5, per to the symmetry
feature of the normal curve,
P(z<=1.5) = P(z>=1.5) = 1P(z<=1.5)

27. Example of Foundry Inc. p.530-
531
• Project completion time T=15 weeks.
• Variance of project time, T2=3.111.
• We want to find the probability that project is finished
within 16 weeks. Here, x=16, and
• So, P(project is finished within 16 weeks)
• = P(z<=Z) = P(z<=0.57) = 0.71566.
57
.
0
76
.
1
1
111
.
3
15
16
2






T
T
x
Z


28. Examples of probability analysis
• If a project’s expected completing time is T=246 days
with its variance T2=25, then what is the probability
that the project:
• is actually completed within 246 days?
• is actually completed within 240 days?
• is actually completed within 256 days?
• is not completed by the 256th day?

29. A Comprehensive Example
• Given the data of a project as in the next slide, answer
the following questions:
• What is PERT network like for this project?
• What is the critical path?
• Activity E will be subcontracted out. What is earliest time it
can be started? What is time it must start so that it will not
delay the project?
• What is probability that the project can be finished within 10
weeks?
• What is the probability that the project is not yet finished
after 12 weeks?

33. Example
Activity
Optimistic
time (to)
Most
likely time
(tm)
Pessimistic
time (tp)
Expected
time (te),
Standard
deviation
(e)
Variance
(e)2
A 4 6 8
B 1 2 3
C 4 4 4
D 4 5 6
E 7 10 16
F 8 9 10
G 2 2 2
H 2 3 7
I 1 3 11
Table 2: Work Breakdown Schedule for Project B

34. Questions
• Calculate the expected activity duration (te),
standard deviation (e) and variance (e)2 for each
activity.
• Assuming that the critical Path is B-E-H = 16 months
• What is the probability of completing the project in 18
months? (nearest estimated number)?
• What is the probability the project will be completed
before the scheduled time (Ts) of 15 months (nearest
estimated number)?