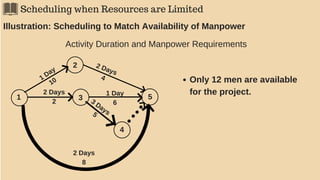
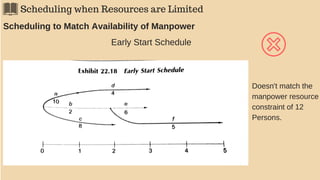
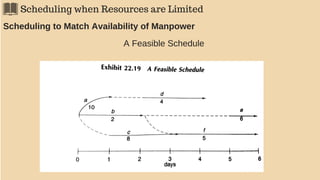
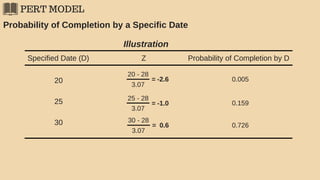
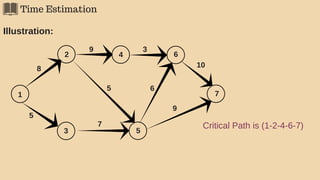
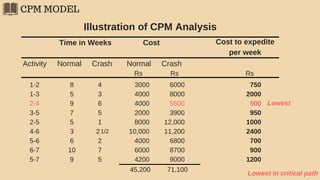
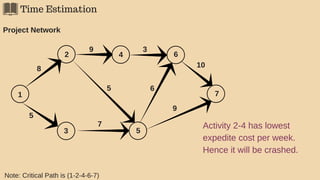
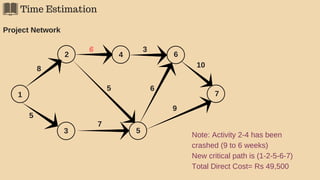
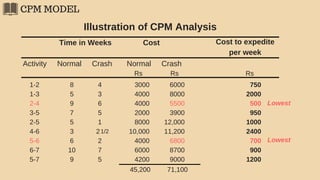
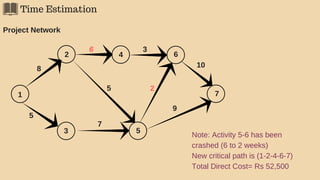
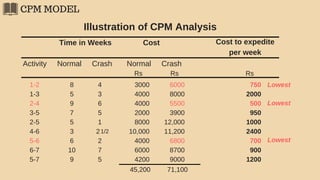
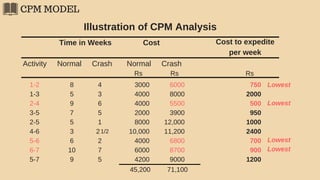
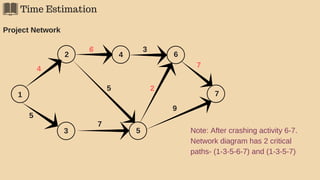
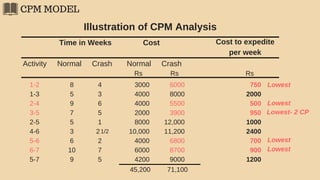
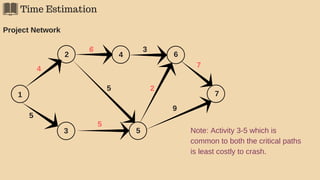
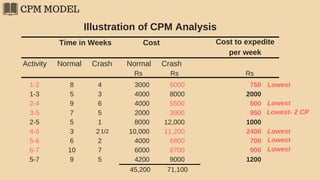
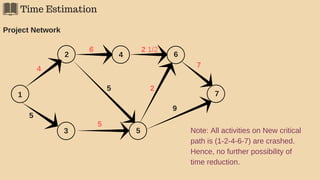
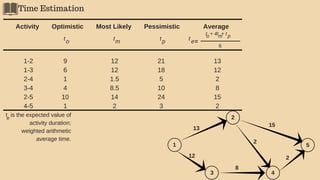
The document discusses project management techniques focusing on developing project networks using diagrams and time estimation methods. It outlines steps for determining critical paths, estimating time values for project activities, and assessing activity floats while considering risk through PERT and cost-time trade-offs with CPM. The purpose is to effectively manage schedules, resources, and project completion timelines.

1. PROJECTS
Figure out what could go wrong before it does: Project Manager.
Network Techniques
For
Project Management
By
Amit Dhyani
Ishan Gandhi

2. Development of Project Network
Step 1:
Network Diagram or Project Graph.
1
2
3 4
Send
Invitations
Prepare
Dinner
Take
Dinner
A Network Diagram shows the activities and
events of the project and their logical
relationships.
Receive
Guests
The Network Diagram can be developed by
using Forward Method or Backward
Method.

3. Development of Project Network
Rules for Network Construction
Each activity must have a preceding and succeeding event.
Each event should have a distinct number.
In previous example, the activity
of "Send Invitations" is
designated as (1-2)
There should be no Loops in the project network.
1
23
Not more than one activity can have the same preceding
and succeeding events.
2
1

4. Time Estimation
Step 2:
Time Estimates for each Activity
Three Time values are obtained from each activity:
1. Optimistic time t
2. Most likely time t
3. Pessimistic time t
o
m
p
it should be obtained by
skipping around the network
rather than by following a
specific path.
they should be defined
independent of one another.
time available for completing
the project should not
influence the estimates.
estimates should considered
allowances which are random
variables and not others.

5. Time Estimation
Network Diagram with average time estimates-
1
2
3 4
5
13
12
8
2
2
15

6. Time Estimation
Activity Optimistic Most Likely Pessimistic Average
t t t to m p e=
t + 4t + to m p
6
1-2
1-3
2-4
3-4
2-5
4-5
9
6
1
4
10
1
12
12
1.5
8.5
14
2
21
18
5
10
24
3
13
12
2
8
15
2
t is the expected value of
activity duration;
weighted arithmetic
average time.
e
1
2
3 4
5
13
12
8
2
2
15

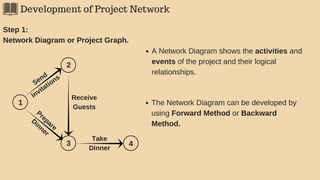
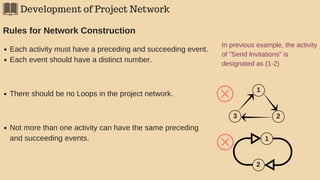
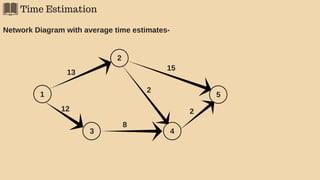
7. Determination of the Critical Path
Step 3
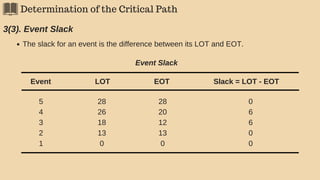
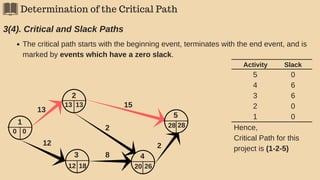
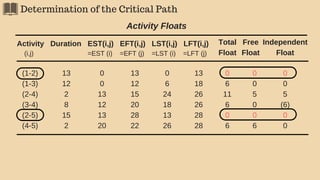
Determining Critical Path/s, event slacks and activity floats.
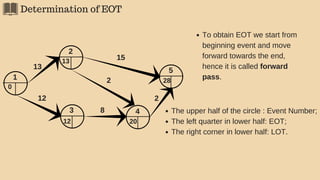
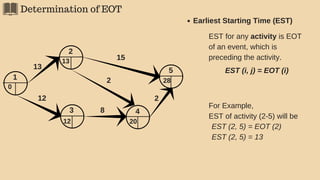
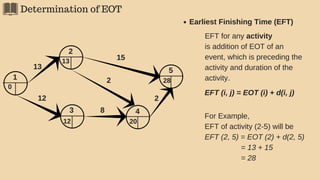
3(1). Earliest Occurrence Time (EOT)
The EOT of an event is the duration of the longest path (from beginning event
whose EOT is set at 0) leading to that event.
Hence, EOT of the end event represents the minimum time required for completing
the project.
General formula for EOT is:
EOT (i) = Max [ EOT (k) + d(k, i) ] Where,
EOT (i)= EOT of i event;
EOT (k)= EOT of k event (k precedes i);
d (k, i)= duration of activity (k, i)
th
th

8. Determination of EOT
5
2
43 8
2
15
2
1
13
12
0
13
12
EOT (i) = Max [ EOT (k) + d(k, i)]
EOT (4)
= Max [ ]
[ EOT (3) + d(3, 4)] [ EOT (2) + d(2, 4)]
= [12 + 8] = [13 + 2]
= [20] = [15]
EOT (4) = 20

9. Determination of EOT
5
2
43 8
2
15
2
1
13
12
0
13
12 20
28
To obtain EOT we start from
beginning event and move
forward towards the end,
hence it is called forward
pass.
The upper half of the circle : Event Number;
The left quarter in lower half: EOT;
The right corner in lower half: LOT.

10. Determination of EOT
5
2
43 8
2
15
2
1
13
12
0
13
12 20
28
Earliest Starting Time (EST)
EST for any activity is EOT
of an event, which is
preceding the activity.
EST (i, j) = EOT (i)
For Example,
EST of activity (2-5) will be
EST (2, 5) = EOT (2)
EST (2, 5) = 13

11. Determination of EOT
5
2
43 8
2
15
2
1
13
12
0
13
12 20
28
Earliest Finishing Time (EFT)
EFT for any activity
is addition of EOT of an
event, which is preceding the
activity and duration of the
activity.
EFT (i, j) = EOT (i) + d(i, j)
For Example,
EFT of activity (2-5) will be
EFT (2, 5) = EOT (2) + d(2, 5)
= 13 + 15
= 28

12. Determination of the Critical Path
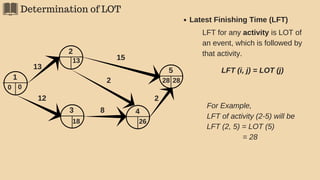
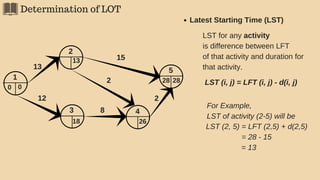
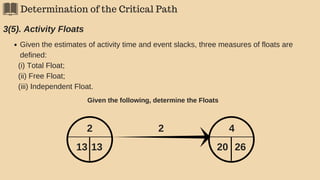
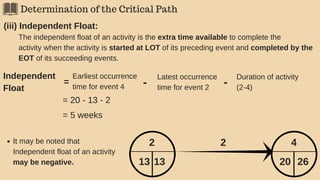
3(2). Latest Occurrence Time (LOT)
The EOT of an event is the latest allowable time by which the event can occur, given
the time that is allowed for completion of the project (occurence of end event).
Hence, LOT of the an event represents the latest time by which the event should
occur to enable the project to be completed in given time.
General formula for LOT is:
LOT (i) = Min [ LOT (j) - d(i, j) ] Where,
LOT (i)= LOT of i event;
LOT (j)= LOT of j event (j follows i);
d (i, j)= duration of activity (i, j)
th
th

13. Determination of LOT
5
2
43 8
2
15
2
1
13
12
28
LOT (i) = Min [ LOT (j) - d(i, j)]
LOT (2)
= MIN [ ]
[ LOT (4) - d(2, 4)] [ LOT (5) - d(2, 5)]
= [26 - 2] = [28 - 15]
= [24] = [13]
LOT (2) = 13
26

14. Determination of LOT
5
2
43 8
2
15
2
1
13
12
0
13
26
28
To obtain LOT we start
from end event and
move backward towards
the beginning, hence it is
called backward pass.
LOT for end event is the given time for the
project to be completed. Normally, EOT is
considered for project deadline.
28
18
0

15. Determination of LOT
5
2
43 8
2
15
2
1
13
12
0
13
26
28 28
18
0
LFT for any activity is LOT of
an event, which is followed by
that activity.
LFT (i, j) = LOT (j)
Latest Finishing Time (LFT)
For Example,
LFT of activity (2-5) will be
LFT (2, 5) = LOT (5)
= 28

16. Determination of LOT
5
2
43 8
2
15
2
1
13
12
0
13
26
28 28
18
0
For Example,
LST of activity (2-5) will be
LST (2, 5) = LFT (2,5) + d(2,5)
= 28 - 15
Latest Starting Time (LST)
LST for any activity
is difference between LFT
of that activity and duration for
that activity.
LST (i, j) = LFT (i, j) - d(i, j)
= 13

17. Determination of the Critical Path
3(3). Event Slack
The slack for an event is the difference between its LOT and EOT.
Event Slack
Event LOT EOT Slack = LOT - EOT
5
4
3
2
1
28
26
18
13
0
28
20
12
13
0
0
6
6
0
0

18. Determination of the Critical Path
3(4). Critical and Slack Paths
The critical path starts with the beginning event, terminates with the end event, and is
marked by events which have a zero slack.
5
2
43 8
2
1
12
0
12 20
28
2
0
13 13
28
2618
13
15
5
4
3
2
1
0
6
6
0
0
Activity Slack
Hence,
Critical Path for this
project is (1-2-5)

19. Determination of the Critical Path
3(5). Activity Floats
Given the estimates of activity time and event slacks, three measures of floats are
defined:
(i) Total Float;
(ii) Free Float;
(iii) Independent Float.
2
13 13
4
20 26
2
Given the following, determine the Floats

20. Determination of the Critical Path
(i) Total Float:
2
13 13
4
20 26
2
The total float of an activity is the extra time available to complete the activity if it is
started as early as possible, without delaying the completion of the project.
Total
Float
=
Latest occurrence
time for event 4
-
Earliest occurrence
time for event 2 -
Duration of activity
(2-4)
= 26 - 13 - 2
= 11 weeks
Activities which have a
Zero Total Float lie
on critical path.

21. Determination of the Critical Path
(ii) Free Float:
2
13 13
4
20 26
2
The free float of an activity is the extra time available to complete the activity when the
activity is started at EOT of its preceding event and completed by the EOT of its
succeeding events.
Free
Float
=
Earliest occurrence
time for event 4 -
Earliest occurrence
time for event 2
-
Duration of activity
(2-4)
= 20 - 13 - 2
= 5 weeks

22. Determination of the Critical Path
(iii) Independent Float:
2
13 13
4
20 26
2
The independent float of an activity is the extra time available to complete the
activity when the activity is started at LOT of its preceding event and completed by the
EOT of its succeeding events.
Independent
Float
=
Earliest occurrence
time for event 4 -
Latest occurrence
time for event 2
-
Duration of activity
(2-4)
= 20 - 13 - 2
= 5 weeks
It may be noted that
Independent float of an activity
may be negative.

23. Determination of the Critical Path
Activity Floats
Activity Duration EST(i,j) EFT(i,j) LST(i,j) LFT(i,j)
(1-2)
(1-3)
(2-4)
(3-4)
(2-5)
(4-5)
13
12
2
8
15
2
(i,j) =EST (i) =EFT (j) =LST (i) =LFT (j)
Total
Float
Free
Float
Independent
Float
0
0
13
12
13
20
13
12
15
20
28
22
0
6
24
18
13
26
13
18
26
26
28
28
0
6
11
6
0
6
0
0
5
0
0
6
0
0
5
(6)
0
0

24. Scheduling when Resources are Limited
The Bounding Schedules
(i) Early Start Schedule:
It refers to the schedule in which all activities start as early as possible-
(a) all activities occur at
their earliest i.e. EST and
EFT.
(b) there may be time lag
between completion of
certain activities and
occurrence of events.
(c) all activities emanating
from an event begins at
same time.
1
3
2
4
5
0 5 15 25 302010

25. Scheduling when Resources are Limited
The Bounding Schedules
(i) Late Start Schedule:
It refers to the schedule in which all activities start as late as possible-
(a) all activities occur at
their Latest i.e. LST
and LFT.
(b) some activities may start
after time lag subsequent to
occurrence of preceding
events.
(c) all activities leading to an
event are completed at
same time.
1
3
2
4
5
0 5 15 25 302010

26. Scheduling when Resources are Limited
Illustration: Scheduling to Match Availability of Manpower
Activity Duration and Manpower Requirements
1
2
3
4
5
2 Days
2
1 Day
10
2 Days
4
1 Day
63 Days5
2 Days
8
Only 12 men are available
for the project.

27. Scheduling when Resources are Limited
Scheduling to Match Availability of Manpower
Early Start Schedule
Doesn't match the
manpower resource
constraint of 12
Persons.

28. Scheduling when Resources are Limited
Scheduling to Match Availability of Manpower
A Feasible Schedule

29. PERT MODEL
Program Evaluation Review Technique (PERT) was originally developed to facilitate
the planning and scheduling of the Polaris Fleet Ballistic Missile project of the US
government.
PERT Model is designed to handle risk and uncertainty.
PERT Model is suitable for-
Introduction
- Research and Development programmes
- Aerospace Projects
- Other projects involving new technology
As in such projects time required for completing various jobs or activities can be highly
variable.
Hence, the orientation of PERT is 'Probabilistic'

30. PERT MODEL
Variability in PERT analysis is measured by variance or standard deviation.
Steps involved in calculating standard deviation of duration of critical path:
Measures of Variability
(i) Determine Standard Deviation of duration of each activity on the critical path.
(ii) Determine S.D. of total duration of critical path on basis of step (i).
=
t - tp o
6
Where,
is Standard Deviation,
t is pessimistic time,
t is optimistic time.
p
o

31. PERT MODEL
Standard Deviation and Variance of Activity Duration
on Critical Path
Activity t t = t - t /6 Variance =p po o
2
(1-2)
(2-5)
21
24
9
10
2
2.33
4.00
5.43
Variance
(critical path duration)
Sum of Variances of activity
durations on the critical path
=
Standard Deviation
(critical path duration)
= (Sum of Variances of activity
durations on the critical path )
1/2
= (4 + 5.43)1/2
= 3.07

32. PERT MODEL
Probability of Completion by a Specific Date
With information of mean (T) and standard deviation ( ) for critical path duration, we can
compute the probability of completion by a specified date (D) as follows:
Z =
D - T
Where,
Z is number of S.D by which D, exceeds T
D is the specified date
T mean critical path duration

33. PERT MODEL
Probability of Completion by a Specific Date
Illustration
Specified Date (D) Z Probability of Completion by D
20
25
30
20 - 28
3.07
= -2.6
25 - 28
3.07
= -1.0
30 - 28
3.07
= 0.6
0.005
0.159
0.726

34. CPM MODEL
Introduction
Critical Path Method (CPM) was developed independently by Du Pont Company to
solve scheduling problems in industrial settings.
CPM Model is primarily concerned with the trade-off between cost and time.
CPM Model is applied to projects that employ a fairly stable technology and are
relatively risk free.
The main thrust of CPM analysis is on time-cost relationships
and it seeks to determine the project schedule which
minimizes total cost.

35. CPM MODEL
Assumptions under CPM Model
1. Two types of costs are associated with the project: Direct Costs and
Indirect Costs.
2. Activities of projects can be expedited (sooner) by crashing which involves
employing more resources.
3. Crashing reduces time but enhances direct costs because of factors like
overtime payments, extra payments and wastage.
4. Indirect costs associated with project increase linearly with project duration.

36. CPM MODEL
Procedure of CPM Analysis
1. Obtain the critical path in the network model. Determine project duration
and direct cost.
2. Examine cost-time slope of activities on the critical path obtained and
crash the activity which has the least slope.
3. Construct the new critical path after crashing as per step 2. Determine
project duration and cost.
4. Repeat step 2 and 3 till activities on the critical path are crashed.

37. Time Estimation
Illustration:
1
2
3
4
5
8
6
9
5
3
5
6
7
7
10
9
Critical Path is (1-2-4-6-7)

38. CPM MODEL
Illustration of CPM Analysis
Time in Weeks Cost Cost to expedite
per week
Activity Normal Crash Normal Crash
Rs Rs Rs
1-2
1-3
2-4
3-5
2-5
4-6
5-6
6-7
5-7
8
5
9
7
5
3
6
10
9
4
3
6
5
1
2
2
7
5
1/2
3000
4000
4000
2000
8000
10,000
4000
6000
4200
6000
8000
5500
3900
12,000
11,200
6800
8700
9000
750
2000
500
950
1000
2400
700
900
1200
45,200 71,100
Lowest
Lowest in critical path

39. Time Estimation
Project Network
1
2
3
4
5
8
6
9
5
3
5
6
7
7
10
9
Activity 2-4 has lowest
expedite cost per week.
Hence it will be crashed.
Note: Critical Path is (1-2-4-6-7)

40. Time Estimation
Project Network
1
2
3
4
5
8
6
6
5
3
5
6
7
7
10
9
Note: Activity 2-4 has been
crashed (9 to 6 weeks)
New critical path is (1-2-5-6-7)
Total Direct Cost= Rs 49,500

41. CPM MODEL
Illustration of CPM Analysis
Time in Weeks Cost Cost to expedite
per week
Activity Normal Crash Normal Crash
Rs Rs Rs
1-2
1-3
2-4
3-5
2-5
4-6
5-6
6-7
5-7
8
5
9
7
5
3
6
10
9
4
3
6
5
1
2
2
7
5
1/2
3000
4000
4000
2000
8000
10,000
4000
6000
4200
6000
8000
5500
3900
12,000
11,200
6800
8700
9000
750
2000
500
950
1000
2400
700
900
1200
45,200 71,100
Lowest
Lowest

42. Time Estimation
Project Network
1
2
3
4
5
8
2
6
5
3
5
6
7
7
10
9
Note: Activity 5-6 has been
crashed (6 to 2 weeks)
New critical path is (1-2-4-6-7)
Total Direct Cost= Rs 52,500

43. CPM MODEL
Illustration of CPM Analysis
Time in Weeks Cost Cost to expedite
per week
Activity Normal Crash Normal Crash
Rs Rs Rs
1-2
1-3
2-4
3-5
2-5
4-6
5-6
6-7
5-7
8
5
9
7
5
3
6
10
9
4
3
6
5
1
2
2
7
5
1/2
3000
4000
4000
2000
8000
10,000
4000
6000
4200
6000
8000
5500
3900
12,000
11,200
6800
8700
9000
750
2000
500
950
1000
2400
700
900
1200
45,200 71,100
Lowest
Lowest
Lowest

44. CPM MODEL
Illustration of CPM Analysis
Time in Weeks Cost Cost to expedite
per week
Activity Normal Crash Normal Crash
Rs Rs Rs
1-2
1-3
2-4
3-5
2-5
4-6
5-6
6-7
5-7
8
5
9
7
5
3
6
10
9
4
3
6
5
1
2
2
7
5
1/2
3000
4000
4000
2000
8000
10,000
4000
6000
4200
6000
8000
5500
3900
12,000
11,200
6800
8700
9000
750
2000
500
950
1000
2400
700
900
1200
45,200 71,100
Lowest
Lowest
Lowest
Lowest

45. Time Estimation
Project Network
1
2
3
4
5
4
2
6
5
3
5
6
7
7
7
9
Note: After crashing activity 6-7.
Network diagram has 2 critical
paths- (1-3-5-6-7) and (1-3-5-7)

46. CPM MODEL
Illustration of CPM Analysis
Time in Weeks Cost Cost to expedite
per week
Activity Normal Crash Normal Crash
Rs Rs Rs
1-2
1-3
2-4
3-5
2-5
4-6
5-6
6-7
5-7
8
5
9
7
5
3
6
10
9
4
3
6
5
1
2
2
7
5
1/2
3000
4000
4000
2000
8000
10,000
4000
6000
4200
6000
8000
5500
3900
12,000
11,200
6800
8700
9000
750
2000
500
950
1000
2400
700
900
1200
45,200 71,100
Lowest
Lowest
Lowest
Lowest
Lowest- 2 CP

47. Time Estimation
Project Network
1
2
3
4
5
4
2
6
5
3
5
6
5
7
7
9
Note: Activity 3-5 which is
common to both the critical paths
is least costly to crash.

48. CPM MODEL
Illustration of CPM Analysis
Time in Weeks Cost Cost to expedite
per week
Activity Normal Crash Normal Crash
Rs Rs Rs
1-2
1-3
2-4
3-5
2-5
4-6
5-6
6-7
5-7
8
5
9
7
5
3
6
10
9
4
3
6
5
1
2
2
7
5
1/2
3000
4000
4000
2000
8000
10,000
4000
6000
4200
6000
8000
5500
3900
12,000
11,200
6800
8700
9000
750
2000
500
950
1000
2400
700
900
1200
45,200 71,100
Lowest
Lowest
Lowest
Lowest
Lowest- 2 CP
Lowest

49. Time Estimation
Project Network
1
2
3
4
5
4
2
6
5
2 1/2
5
6
5
7
7
9
Note: All activities on New critical
path is (1-2-4-6-7) are crashed.
Hence, no further possibility of
time reduction.

50. CPM MODEL
Activities Crashed
None
(2-4)
(2-4) and (5-6)
(1-2), (2-4) and (5-6)
(1-2), (2-4), (5-6) and (6-7)
(1-2), (2-4), (3-5), (5-6) and (6-7)
(1-2), (2-4), (3-5), (5-6), (4-6) and (6-7)
Project
Duration
In weeks
Total
Direct
Cost
Total
Indirect
Cost
Total Cost
30
29
27
24
21
20
19
1/2
45200
46700
49500
52500
55200
57100
58300
60000
58000
54000
48000
42000
40000
39000
105,200
104,700
103,500
100,500
97,200
97,100
97,300
Project Duration and Total Cost
Indirect Cost is Rs 2000 per week

51. Network Cost System
Introduction
Network Cost System was developed to provide vehicle for cost
planning and control of projects.
Basic principle is: Costs are planned, measured, analysed and
controlled in terms of project activities.
For cost projections it is assumed that the expenditure for any activity
is incurred evenly over the duration of activity.

52. Network Cost System
Analysis and Control of Costs
1. Cost incurred to date
In NCS, Cost are recorded activity wise. Costs incurred to date can be obtained by
summing up costs for various activities.
2. Budgeted cost to date
is the cost projections made at the beginning.
3. Value of work done to date
is equal to budgeted costs * percentage of work accomplished.
4. Cost over-run (under-run) to date
Actual Cost - Value of work completed
Vaue of work completed
* 100

53. Network Cost System
Analysis and Control of Costs
5. Time over-run (under-run) to date
Time over-run is usually defined in terms of months behind or months ahead.

54. THANK YOU