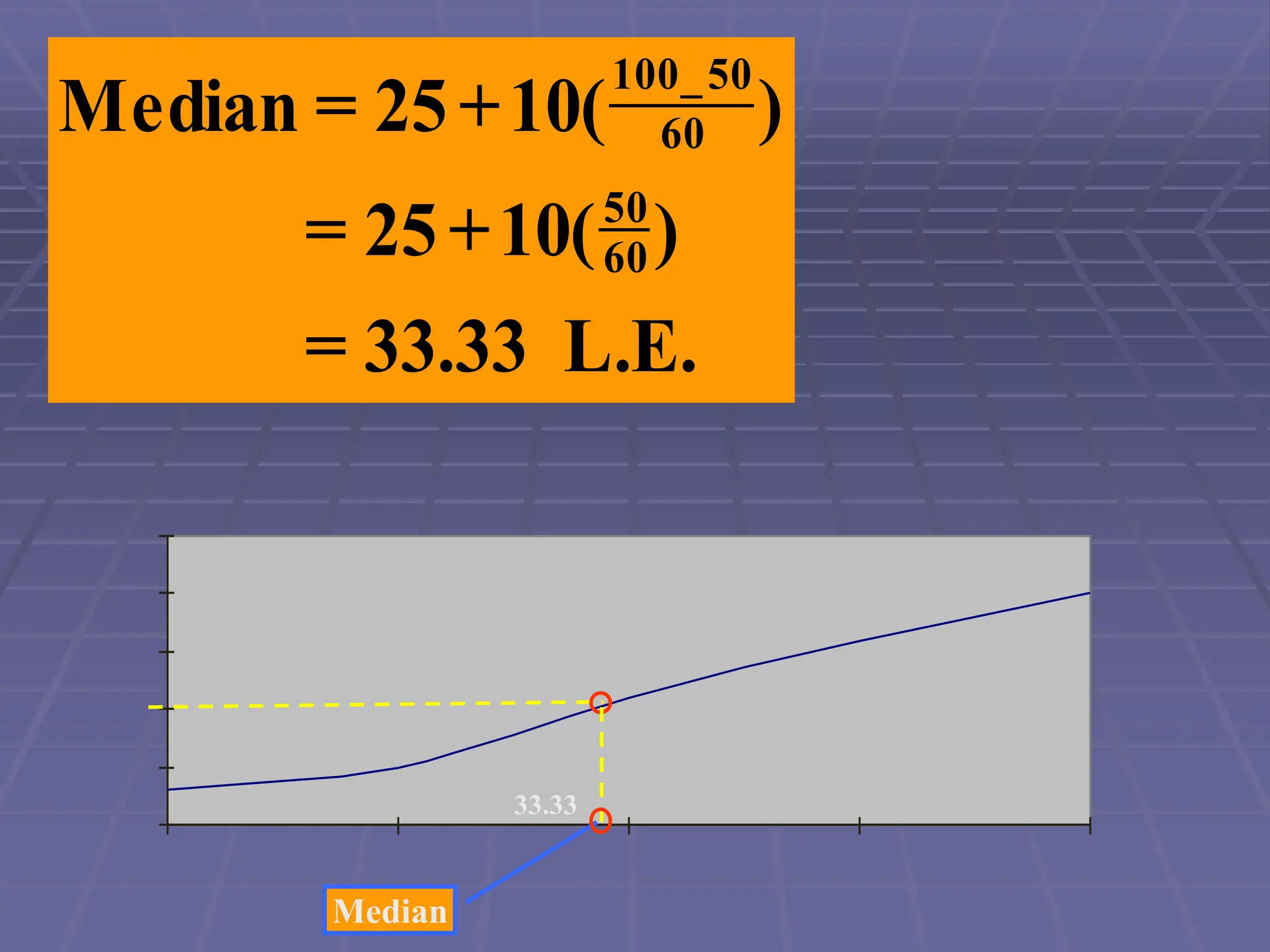
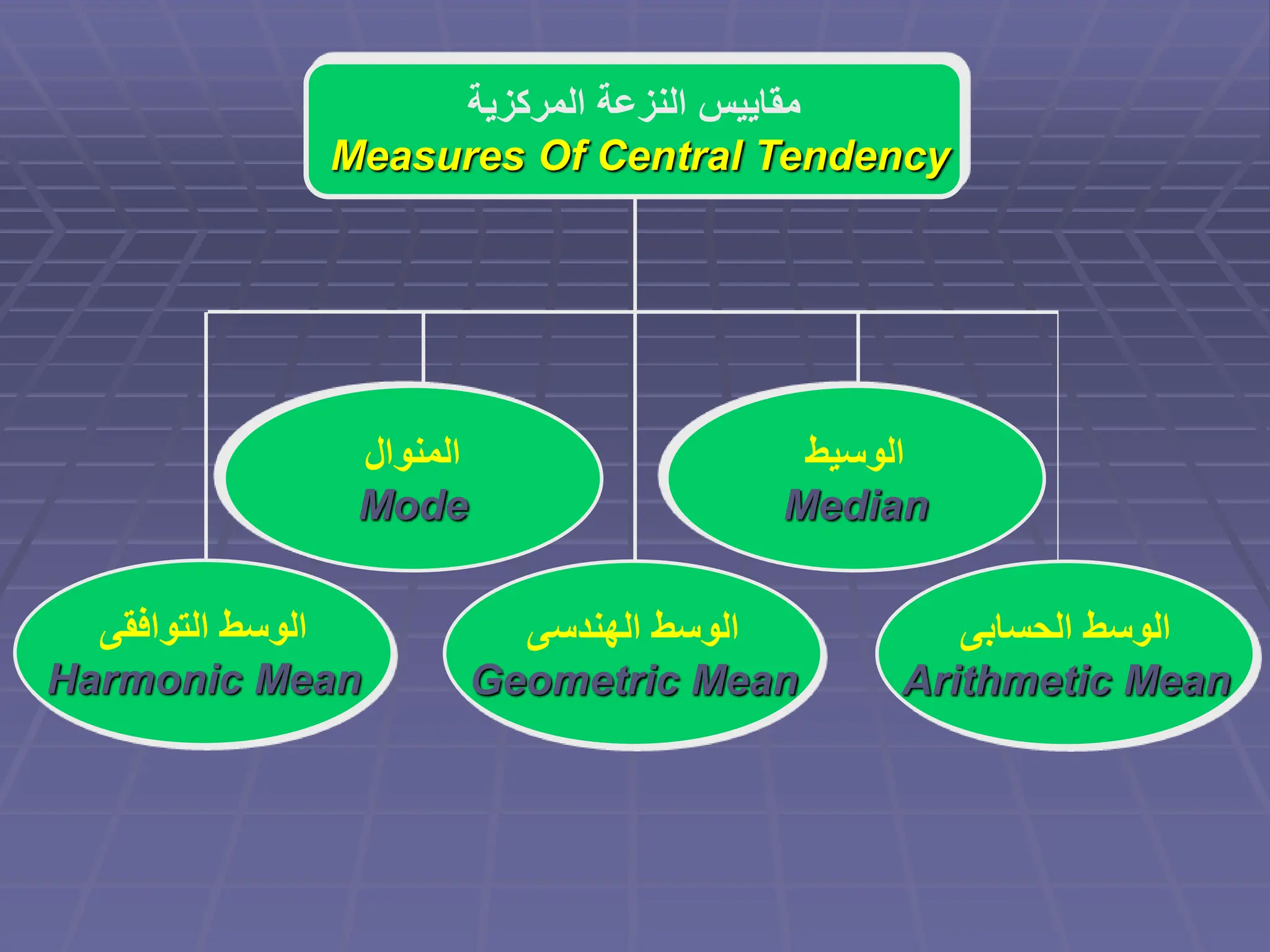
تناقش الوثيقة مقاييس النزعة المركزية التي تعكس كيفية تجمع البيانات حول نقطة متوسطة. تشمل هذه المقاييس الوسط الحسابي، الهندسي، والتوافقي، ويتم استخدامها لتحليل البيانات المختلفة في الحياة اليومية. كما تتناول الوثيقة كيفية حساب هذه المقاييس وتأثير القيم الشاذة على النتائج.

1. Measures Of
Central Tendency

2. *
‫المستخدمة‬ ‫المقاييس‬ ‫وتسمى‬
‫المركزية‬ ‫النزعة‬ ‫مقاييس‬
‫نقطة‬ ‫حول‬ ‫للتجمع‬ ‫ميل‬ ‫لها‬ ‫العامة‬ ‫الحياة‬ ‫فى‬ ‫ظاهرة‬ ‫كل‬
‫؛‬ ‫معينة‬
‫سنصل‬ ‫فإننا‬ ‫النقطة‬ ‫هذه‬ ‫تحديد‬ ‫استطعنا‬ ‫إذا‬ ‫ثم‬ ‫ومن‬
‫إلى‬
‫القيم‬ ‫حولها‬ ‫تتجمع‬ ‫متوسطة‬ ‫قيمة‬
.
*
‫القي‬ ‫هذه‬ ‫حول‬ ‫التجمع‬ ‫إلى‬ ‫الميل‬ ‫ذلك‬ ‫يسمى‬
‫مة‬
‫المركزية‬ ‫بالنزعة‬

3. •
‫البيانات‬ ‫دقة‬ ‫على‬ ‫تؤثر‬ ‫ال‬ ‫سهلة‬ ‫بطريقة‬ ‫يحسب‬
.
•
‫لها‬ ‫المقياس‬ ‫حساب‬ ‫المطلوب‬ ‫المفردات‬ ‫جميع‬ ‫االعتبار‬ ‫فى‬ ‫يأخذ‬
.
•
‫العامة‬ ‫الحياة‬ ‫فى‬ ‫يستخدم‬ ‫مفهوم‬ ‫طبيعى‬ ‫معنى‬ ‫له‬ ‫يكون‬
.
•
‫حسابه‬ ‫طرق‬ ‫بتغير‬ ‫يتغير‬ ‫وال‬ ، ‫الظاهرة‬ ‫فى‬ ‫التغير‬ ‫يعكس‬
.
•
‫تاما‬ ‫خضوعا‬ ‫الجبرية‬ ‫للعمليات‬ ‫يخضع‬
.
•
‫المتطرفة‬ ‫او‬ ‫الشاذة‬ ‫بالقيم‬ ‫يتأثر‬ ‫ال‬
.
•
‫الواحد‬ ‫الحجم‬ ‫ذات‬ ‫العينات‬ ‫باختالف‬ ‫يتأثر‬ ‫ال‬
.

4. ‫المركزية‬ ‫النزعة‬ ‫مقاييس‬
Measures Of Central Tendency
‫الحسابى‬ ‫الوسط‬
Arithmetic Mean
‫التوافقى‬ ‫الوسط‬
Harmonic Mean
‫الهندسى‬ ‫الوسط‬
Geometric Mean
‫الوسيط‬
Median
‫المنوال‬
Mode

5. ‫بسيط‬ ‫انه‬ ‫حيث‬ ‫االحصاء‬ ‫فى‬ ‫المستخدمة‬ ‫المقاييس‬ ‫أكثر‬ ‫من‬ ‫يعد‬
‫وسهل‬
‫المجموعات‬ ‫بين‬ ‫للمقارنة‬ ‫يصلح‬ ‫و‬ ‫الفهم‬
.
Arithmetic Mean ‫الحسابى‬ ‫الوسط‬
‫وال‬‫أ‬
:
‫المبوبة‬ ‫غير‬ ‫البيانات‬ ‫حالة‬ ‫فى‬
:-
‫المتغير‬ ‫قيم‬ ‫كانت‬ ‫إذا‬
(x)
‫هـــى‬
x1 , x2 , … , xn
‫حيث‬
(n)
‫حجم‬ ‫يمثل‬
‫التالى‬ ‫النحو‬ ‫على‬ ‫عنه‬ ‫التعبير‬ ‫يمكن‬ ‫الحسابى‬ ‫الوسط‬ ‫فإن‬ ‫؛‬ ‫المجموعة‬
:-
n
x
Σ
=
= n
x
+
...
+
x
+
x n
2
1
x

6. ‫مثال‬
‫للقيم‬ ‫الحسابى‬ ‫الوسط‬ ‫احسب‬
2
،
4
،
6
،
1
25
.
3
=
4
1
+
6
+
4
+
2
=
X ‫يتأثر‬ ‫الحسابى‬ ‫الوسط‬
‫والجمع‬ ‫بالطرح‬
‫للقيم‬ ‫الحسابى‬ ‫فالوسط‬
X1+a ,X2+a ,… ,Xn+a
‫يكون‬
:-
a
+
n
x
Σ
=
x
‫مثال‬
‫للقيم‬ ‫الحسابى‬ ‫الوسط‬ ‫احسب‬
3،5،7،2
1
+
25
.
3
=
25
.
4
=
4
2
+
7
+
5
+
3
=
x ‫يتأثر‬ ‫الحسابى‬ ‫الوسط‬
‫القسمة‬ ‫و‬ ‫بالضرب‬
‫للقيم‬ ‫الحسابى‬ ‫فالوسط‬
X1*b ,X2*b ,… ,Xn*b
‫يكون‬
:-
b
*
n
x
Σ
=
x
‫مثال‬
‫للقيم‬ ‫الحسابى‬ ‫الوسط‬ ‫احسب‬
6،10،14،4
2
*
25
.
4
=
5
.
8
=
4
4
+
14
+
10
+
6
=
x

7. ‫ثانيا‬
:
‫المبوبة‬ ‫البيانات‬ ‫حالة‬ ‫فى‬
:-
‫التكرارى‬ ‫التوزيع‬ ‫جدول‬ ‫فى‬ ‫البيانات‬ ‫ألن‬ ‫ذلك‬ ‫؛‬ ‫جديد‬ ‫نوع‬ ‫من‬ ‫صعوبة‬ ‫تواجهنا‬ ‫هنا‬
‫تكون‬
‫فئات‬ ‫فى‬ ‫الختصارها‬ ‫نظرا‬ ‫أجماال‬ ‫معروفة‬ ‫هى‬ ‫بل‬ ، ‫بالتفصيل‬ ‫معروفة‬ ‫غير‬
.
‫؛‬ ‫الفئة‬ ‫مدى‬ ‫على‬ ‫عادال‬ ‫توزيعا‬ ‫موزعة‬ ‫فئة‬ ‫كل‬ ‫فى‬ ‫المفردات‬ ‫كل‬ ‫ان‬ ‫سنفترض‬ ‫لذلك‬
‫الفئة‬ ‫مركز‬ ‫عند‬ ‫متجمعة‬ ‫تكون‬ ‫فئة‬ ‫كل‬ ‫فى‬ ‫المفردات‬ ‫اعتبرنا‬ ‫اذا‬ ‫كثيرا‬ ‫نخطئ‬ ‫لن‬ ‫اننا‬ ‫اى‬
.
‫الفئة‬ ‫مركز‬
=
‫للفئة‬ ‫األدنى‬ ‫الحد‬
+
‫للف‬ ‫األعلى‬ ‫الحد‬
‫ئة‬
2
‫التكراري‬ ‫للتوزيعات‬ ‫الحسابى‬ ‫الوسط‬ ‫يعرف‬ ‫ذلك‬ ‫وعلى‬
‫نة‬ ‫بأ‬ ‫ة‬
‫بالتكرارات‬ ‫المرجح‬ ‫الحسابى‬ ‫الوسط‬
.

8. ‫الفئات‬ ‫لمراكز‬ ‫الحسابى‬ ‫الوسط‬
X1, X2,… ,Xn
‫المناظرة‬ ‫بالتكرارات‬ ‫والمرجح‬
F1,F2,…,Fn
‫يكون‬
F
FX
=
Σ
Σ
x
‫مثال‬
‫مائتين‬ ‫فى‬ ‫بالجنية‬ ‫للعامل‬ ‫األسبوعى‬ ‫األجر‬ ‫يمثل‬ ‫التالى‬ ‫الجدول‬
‫محل‬
‫الخيمة‬ ‫شبرا‬ ‫بمنطقة‬
:-
‫المطلوب‬
‫للعامل‬ ‫األسبوعى‬ ‫األجر‬ ‫متوسط‬ ‫حساب‬
‫بالجنية‬ ‫األسبوعي‬ ‫األجر‬
- 5
- 15
- 25
- 35
55 - 45
‫المجموع‬
‫المحالت‬ ‫عدد‬
30
20
60
50
40
200
‫الحسابى‬ ‫الوسط‬ ‫خصائص‬ ‫من‬ ‫االستفادة‬ ‫يمكن‬
‫طرق‬ ‫بثالث‬ ‫المثال‬ ‫حل‬ ‫فى‬
‫الحساب‬ ‫ســـــــــرعة‬ ‫لتحسين‬

9. ‫المطولة‬ ‫الطريقة‬
5
.
32
=
200
6500
=
F
FX
=
Σ
Σ
X
‫هو‬ ‫للعامل‬ ‫األسبوعى‬ ‫األجر‬ ‫متوسط‬ ‫أن‬ ‫أى‬
32.5
‫جنية‬

10. ‫المختصرة‬ ‫الطريقة‬
‫وهنا‬
‫نطرح‬
‫فرضيا‬ ‫وسطا‬
(
‫ثابت‬ ‫مقدار‬
)
‫مراكز‬ ‫من‬
‫ثم‬ ‫الفئات‬
‫إضافته‬ ‫نعيد‬
‫ب‬ ‫الحسابى‬ ‫الوسط‬ ‫إلى‬
‫حسابه‬ ‫عد‬
‫الفئات‬ ‫مراكز‬ ‫من‬
(
‫المعدلة‬
) .
‫عندما‬ ‫الحساب‬ ‫فى‬ ‫الصعوبات‬ ‫على‬ ‫للتغلب‬ ‫وذلك‬
‫كبيرة‬ ‫أرقام‬ ‫الفئات‬ ‫مراكز‬ ‫تكون‬
‫أو‬
‫كسرية‬
.
5
.
32
=
30
+
200
500
=
30
+
F
1
FX
=
Σ
Σ
X

11. ‫اختصارا‬ ‫األكثر‬ ‫الطريقة‬
‫وهنا‬
‫نقسم‬
‫المعدلة‬ ‫الفئات‬ ‫مراكز‬
(
‫سابقا‬
)
‫على‬
‫ثم‬ ‫ثابت‬ ‫مقدار‬
‫ضربة‬ ‫نعيد‬
‫الحسابى‬ ‫الوسط‬ ‫فى‬
‫الفئات‬ ‫مراكز‬ ‫من‬ ‫حسابه‬ ‫بعد‬
(
‫النهائية‬
( .
5
.
32
=
30
+
10
*
200
50
=
30
+
10
*
F
2
FX
=
Σ
Σ
X
‫عموما‬
‫منتظما‬ ‫التكرارى‬ ‫الجدول‬ ‫كان‬ ‫إذا‬
(
‫متساوية‬ ‫الفئات‬ ‫أطوال‬
(
‫فئة‬ ‫اى‬ ‫أمام‬ ‫صفر‬ ‫وضع‬ ‫يمكن‬ ‫فأنة‬
،
‫االرقام‬ ‫ووضع‬
-
1
،
-
2
،
-
3
،
...
‫الفئة‬ ‫لهذه‬ ‫السابقة‬ ‫الفئات‬ ‫أمام‬
،
‫االرقام‬ ‫ووضع‬
1،2
،
…
‫لها‬ ‫التالية‬ ‫الفئات‬ ‫أمام‬
.
‫أخر‬ ‫مقياس‬

12. Geometric Mean ‫الهندسى‬ ‫الوسط‬
‫وال‬‫أ‬
:
‫المبوبة‬ ‫غير‬ ‫البيانات‬ ‫حالة‬ ‫فى‬
:-
‫المتغير‬ ‫قيم‬ ‫كانت‬ ‫إذا‬
(x)
‫هـــى‬
x1 , x2 , … , xn
‫حيث‬
(n)
‫حجم‬ ‫يمثل‬
‫التالى‬ ‫النحو‬ ‫على‬ ‫عنه‬ ‫التعبير‬ ‫يمكن‬ ‫الهندسى‬ ‫الوسط‬ ‫فإن‬ ‫؛‬ ‫المجموعة‬
:-
n
n
2
1 x
*
...
*
x
*
x
=
G ‫باالستعانة‬
‫باللوغاريتمات‬
n
Log
=
Log
x
Σ
G

13. ‫مثال‬
‫للقيم‬ ‫الحسابى‬ ‫الوسط‬ ‫و‬ ‫الهندسى‬ ‫الوسط‬ ‫احسب‬
2،4،2،16
4
=
256
=
16
*
2
*
4
*
2
=
G 4
4
4
=
602
.
0
=
4
16
Log
+
2
Log
+
4
Log
+
2
Log
=
Log
G
G
6
=
4
24
=
4
16
+
2
+
4
+
2
=
X ‫الحظ‬
‫أن‬
‫من‬ ‫أكبر‬ ‫دائما‬ ‫الحسابى‬ ‫الوسط‬
‫الهندسى‬ ‫الوسط‬
(
‫البيانات‬ ‫لنفس‬
(

14. ‫ثانيا‬
:
‫المبوبة‬ ‫البيانات‬ ‫حالة‬ ‫فى‬
:-
‫الفئات‬ ‫لمراكز‬ ‫الهندسى‬ ‫الوسط‬
X1, X2,… ,Xn
‫المناظرة‬ ‫بالتكرارات‬ ‫والمرجح‬
F1,F2,…,Fn
‫يكون‬
n
n
n
2
2
1
1 F
X
*
...
*
F
X
*
F
X
=
G
F
)
LogX
(
F
=
Log
Σ
Σ
G

15. ‫مثال‬
‫التالى‬ ‫التكرارى‬ ‫الجدول‬ ‫من‬ ‫الهندسى‬ ‫الوسط‬ ‫احسب‬
:-
58
.
14
=
G
16
.
1
=
20
27
.
23
=
LogG
‫أخر‬ ‫مقياس‬

16. ‫الحسابى‬ ‫الوسط‬ ‫مقلوب‬ ‫هو‬ ‫القيم‬ ‫من‬ ‫لمجموعه‬ ‫التوافقى‬ ‫الوسط‬
‫القيم‬ ‫هذه‬ ‫لمقلوبات‬
.
Harmonic Mean ‫التوافق‬ ‫الوسط‬
‫ى‬
‫وال‬‫أ‬
:
‫المبوبة‬ ‫غير‬ ‫البيانات‬ ‫حالة‬ ‫فى‬
:-
‫المتغير‬ ‫قيم‬ ‫كانت‬ ‫إذا‬
(x)
‫هـــى‬
x1 , x2 , … , xn
‫حيث‬
(n)
‫حجم‬ ‫يمثل‬
‫التالى‬ ‫النحو‬ ‫على‬ ‫عنه‬ ‫التعبير‬ ‫يمكن‬ ‫التوافقى‬ ‫الوسط‬ ‫فإن‬ ‫؛‬ ‫المجموعة‬
:-
x
1
=
n
x
1
+
...
+
2
x
1
+
1
x
1
=
Σ
n
n
H

17. ‫مثال‬
‫الحساب‬ ‫الوسط‬ ‫و‬ ‫الهندسى‬ ‫الوسط‬ ‫و‬ ‫التوافقى‬ ‫الوسط‬ ‫احسب‬
‫ى‬
‫للقيم‬
10،20،40،50
15
.
25
=
400000
=
50
*
40
*
20
*
10
=
G 4
4
5
.
20
=
195
.
4
=
50
1
+
40
1
+
20
1
+
10
1
4
=
H
30
=
4
120
=
4
50
+
40
+
20
+
10
=
X
‫الحظ‬
‫أن‬
‫دائما‬
‫من‬ ‫أكبر‬ ‫الحسابى‬ ‫الوسط‬
‫من‬ ‫أكبر‬ ‫الهندسى‬ ‫الوسط‬
‫التوافقى‬ ‫الوسط‬
(
‫البيانات‬ ‫لنفس‬
(
X
<
G
<
H

18. ‫ثانيا‬
:
‫المبوبة‬ ‫البيانات‬ ‫حالة‬ ‫فى‬
:-
‫الفئات‬ ‫لمراكز‬ ‫التوافقى‬ ‫الوسط‬
X1, X2,… ,Xn
‫المناظرة‬ ‫بالتكرارات‬ ‫والمرجح‬
F1,F2,…,Fn
‫يكون‬
X
F
F
=
Σ
Σ
H
‫مع‬ ‫التعامل‬ ‫حالة‬ ‫فى‬ ‫التوافقى‬ ‫الوسط‬ ‫استخدام‬
‫القياسية‬ ‫األسعار‬
‫أو‬
‫عات‬ ‫السر‬ ‫معدالت‬
‫أو‬
‫التغ‬ ‫معدالت‬
‫ير‬
‫يفضل‬

19. ‫مثال‬
‫الت‬ ‫يوضح‬ ‫والذى‬ ‫التالى‬ ‫الجدول‬ ‫من‬ ‫التوافقى‬ ‫الوسط‬ ‫احسب‬
‫وزيع‬
‫عات‬ ‫لسر‬ ‫التكرارى‬
100
‫متسابق‬
:-
h
Km
25
.
9
=
84
.
10
100
=
H ‫أخر‬ ‫مقياس‬

20. ‫الوسيط‬
‫ترتي‬ ‫بعد‬ ‫البيانات‬ ‫منتصف‬ ‫فى‬ ‫الموجودة‬ ‫القيمة‬ ‫هو‬
‫بها‬
(
‫تنازليا‬ ‫أو‬ ‫تصاعديا‬
) .
Median ‫الوسيط‬
‫وال‬‫أ‬
:
‫المبوبة‬ ‫غير‬ ‫البيانات‬ ‫حالة‬ ‫فى‬
:-
‫المتغير‬ ‫قيم‬ ‫كانت‬ ‫إذا‬
(x)
‫هـــى‬
x1 , x2 , … , xn
‫حيث‬
(n)
‫حجم‬ ‫يمثل‬
‫فإن‬ ‫؛‬ ‫المجموعة‬
‫الوسيط‬
‫يكون‬
‫رتبتها‬ ‫التى‬ ‫المفردة‬ ‫هو‬
(
‫الترتيب‬ ‫بعد‬
(
‫ألوسيط‬ ‫تبة‬‫ر‬
= n + 1
2
‫فردى‬‫ألقيم‬‫عدد‬
‫جى‬‫و‬‫ز‬‫ألقيم‬‫عدد‬
‫هما‬‫تبتان‬‫ر‬‫له‬‫ألوسيط‬
n & n + 1
2 2

21. ‫مثال‬
‫للقيم‬ ‫الوسيط‬ ‫احسب‬
112،3،4،5،6
‫التصاعدى‬ ‫الترتيب‬
‫للقيم‬
( ) ( ) ( ) ( ) ( )5
4
3
2
1 112
&
6
&
5
&
4
&
3
[ ]
3
=
2
1
+
5
=
Order
Median
odd
5
=
n
‫يتأثر‬ ‫لم‬ ‫الوسيط‬
‫الشاذة‬ ‫بالقيمة‬
112
‫مثال‬
‫للقيم‬ ‫الوسيط‬ ‫احسب‬
-
3
،
-
1،3،6،7،8
(-3)1& (-1)2& (3)3& (6)4& (7)5& (8)6
4
&
3
=
1
+
2
6
&
2
6
=
Orders
Median
]
even
[
6
=
n
5
=
Median
5
.
4
=
2
6
+
3
=
Median

22. ‫ثانيا‬
:
‫المبوبة‬ ‫البيانات‬ ‫حالة‬ ‫فى‬
:-
‫يجب‬
‫الهابط‬ ‫أو‬ ‫الصاعد‬ ‫المتجمعين‬ ‫التكراريين‬ ‫الجدولين‬ ‫أحد‬ ‫من‬ ‫الوسيط‬ ‫حساب‬
‫الوسيط‬
‫هو‬
‫القيمة‬
‫المقابلة‬
‫التكرارات‬ ‫مجموع‬ ‫لنصف‬
.
‫ألوسيط‬ ‫تبة‬‫ر‬
=
2
F
Σ ‫لذلك‬
*
‫ألصاعد‬‫ألمتجمع‬‫ى‬‫أر‬‫ر‬‫ألتك‬‫ألجدول‬‫من‬‫ألحساب‬‫حالة‬‫فى‬
(
‫تكوينه‬‫بعد‬
)
‫الوسيط‬
=
‫الوسيط‬ ‫لفئة‬ ‫األدنى‬ ‫الحد‬
+
‫الوسيط‬ ‫فئة‬ ‫طول‬
(
‫الوسيط‬ ‫رتبة‬
-
‫الساب‬ ‫الصاعد‬ ‫المتجمع‬ ‫التكرار‬
‫الوسيط‬ ‫لفئة‬ ‫ق‬
(
‫الوسيط‬ ‫لفئة‬ ‫األصلى‬ ‫التكرار‬

23. ‫مثال‬
‫مائتين‬ ‫فى‬ ‫بالجنية‬ ‫للعامل‬ ‫األسبوعى‬ ‫األجر‬ ‫يمثل‬ ‫التالى‬ ‫الجدول‬
‫محل‬
‫الخيمة‬ ‫شبرا‬ ‫بمنطقة‬
:-
‫المطلوب‬
‫الوسيط‬ ‫باستخدام‬ ‫للعامل‬ ‫األسبوعى‬ ‫األجر‬ ‫متوسط‬ ‫حساب‬
.
‫بالجنية‬ ‫األسبوعي‬ ‫األجر‬
5
-
15
-
25
-
35
-
45
-
55
‫المجموع‬
‫المحالت‬ ‫عدد‬
30
20
60
50
40
200
‫ألوسيط‬‫تبة‬‫ر‬
100
=
2
200
=
2
F
Σ
=

24. .
E
.
L
33
.
33
=
)
(
10
+
25
=
)
(
10
+
25
=
Median
60
50
60
50
_
100
Median
33.33

25. •
‫الشاذة‬ ‫القيم‬ ‫بها‬ ‫تكثر‬ ‫التى‬ ‫البيانات‬
.
•
‫كليهما‬ ‫من‬ ‫أو‬ ‫طرفيها‬ ‫أحد‬ ‫من‬ ‫المفتوحة‬ ‫التكرارية‬ ‫الجداول‬
.
•
‫الفئات‬ ‫طول‬ ‫فى‬ ‫المتساوية‬ ‫غير‬ ‫التكرارية‬ ‫التوزيعات‬
.
‫يفضل‬
‫مع‬ ‫التعامل‬ ‫حالة‬ ‫فى‬ ‫الوسيط‬ ‫استخدام‬
‫أخر‬ ‫مقياس‬

26. ‫المنوال‬
‫البيان‬ ‫بين‬ ‫شيوعا‬ ‫األكثر‬ ‫القيمة‬ ‫هو‬
‫ات‬
.
Mode ‫المنوال‬
‫وال‬‫أ‬
:
‫المبوبة‬ ‫غير‬ ‫البيانات‬ ‫حالة‬ ‫فى‬
:-
‫مثال‬
‫للقيم‬ ‫المنوال‬ ‫احسب‬
2،3،4،2،11،2
‫ألقيمة‬‫هى‬‫أ‬‫ر‬‫أ‬‫ر‬‫تك‬‫ألقيم‬‫ثر‬‫ك‬‫أ‬
2
2
=
Mode
‫المنوال‬
‫الشاذة‬ ‫بالقيم‬ ‫تأثر‬ ‫المركزية‬ ‫النزعة‬ ‫مقاييس‬ ‫أقل‬

27. ‫اعتبار‬ ‫يمكن‬ ‫ال‬
‫المنوال‬
‫مقياسا‬
‫المركزية‬ ‫للنزعة‬
•
‫ة‬‫ر‬‫مكر‬‫قيم‬ ‫هناك‬‫يكن‬‫لم‬‫ن‬‫أ‬
.
•
‫ع‬‫ألشيو‬ ‫نفس‬‫لها‬‫قيمة‬ ‫من‬‫ثر‬‫ك‬‫أ‬‫هناك‬‫كان‬‫ن‬‫أ‬
.
‫مثال‬
3
،
4
،
5
،
6
،
7
‫مثال‬
2
،
3
،
2
،
5
،
3
،
4

28. ‫ثانيا‬
:
‫المبوبة‬ ‫البيانات‬ ‫حالة‬ ‫فى‬
:-
‫المنوال‬
‫تكر‬ ‫ألكبر‬ ‫المقابلة‬ ‫القيمة‬ ‫هو‬
‫ار؛‬
‫تكرار‬ ‫أكبر‬ ‫لها‬ ‫التى‬ ‫للفئة‬ ‫تنتمى‬ ‫والتى‬
(
‫الم‬ ‫الفئة‬
‫نوالية‬
(
‫فأن‬ ‫ذلك‬ ‫وعلى‬
‫المنوال‬
‫المنوالية‬ ‫الفئة‬ ‫فى‬ ‫يقع‬
‫تحت‬
‫التكراريين‬ ‫تأثير‬
‫السابق‬
‫و‬
‫الالحق‬
‫المن‬ ‫للفئة‬
‫والية‬
.
‫الرافعة‬ ‫قانون‬ ‫باستخدام‬ ‫المنوال‬ ‫يحدد‬
:
‫القوة‬
x
‫ذراعها‬
=
‫المقاومة‬
x
‫ذراعها‬

29. ‫مثال‬
‫مائتين‬ ‫فى‬ ‫بالجنية‬ ‫للعامل‬ ‫األسبوعى‬ ‫األجر‬ ‫يمثل‬ ‫التالى‬ ‫الجدول‬
‫محل‬
‫الخيمة‬ ‫شبرا‬ ‫بمنطقة‬
:-
‫المطلوب‬
‫للعامل‬ ‫األسبوعى‬ ‫األجر‬ ‫منوال‬ ‫حساب‬
.
‫بالجنية‬ ‫األسبوعي‬ ‫األجر‬
5
-
15
-
25
-
35
-
45
-
55
‫المجموع‬
‫المحالت‬ ‫عدد‬
30
20
60
50
40
200
‫ألمنوألية‬‫ألفئة‬
=
25
-
35
‫أر‬‫ر‬‫تك‬‫كبر‬‫أ‬ ‫لها‬
(
60
(
20
‫ألسابق‬‫أر‬‫ر‬‫ألتك‬
‫ألمنوأل‬ 25
50
‫ألالحق‬‫أر‬‫ر‬‫ألتك‬
35 ‫ألمنوأل‬‫ألفئة‬‫بدأية‬
‫ية‬
‫ألمنوأل‬‫ألفئة‬ ‫نهاية‬
‫ية‬
‫س‬
10 -
‫س‬

30. 20
)
‫س‬
(
=
50
)
10
_
‫س‬
(
‫س‬
=
70
500
=
14
.
7

‫ألمنوأل‬
=
25
+
7.14
=
32.4
‫جنية‬
‫تحديد‬ ‫يمكن‬
‫المنوال‬
‫بيانيا‬
‫المدرج‬ ‫رسم‬ ‫من‬
‫التكرارى‬

31. ‫التكرارى‬ ‫المدرج‬
0
10
20
30
40
50
60
70
1
5-15 15-25 25-35 35-45 45-55
32.14
Mode
‫أخر‬ ‫مقياس‬