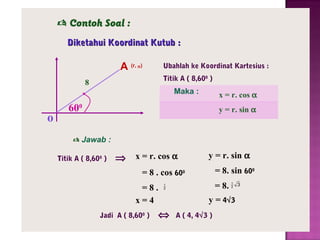
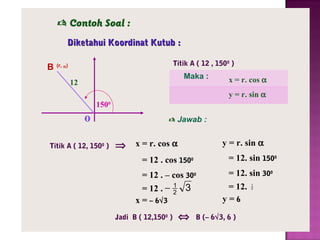
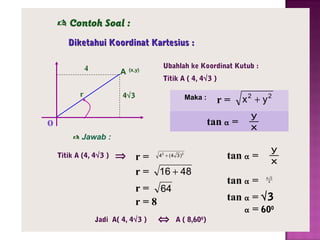
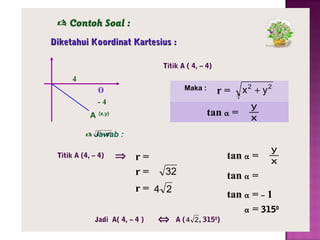
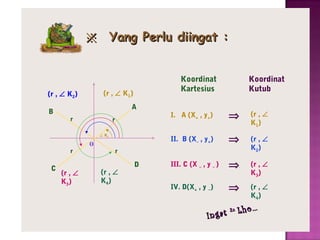
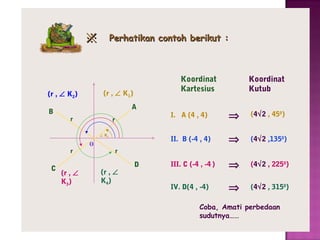
Dokumen ini menjelaskan pengertian dan jenis sistem koordinat, yaitu sistem koordinat kartesius dan koordinat kutub. Sistem koordinat kartesius menggambarkan posisi titik dengan pasangan bilangan (x,y), sementara koordinat kutub menggunakan jarak dan sudut untuk menentukan posisi titik. Hubungan antara kedua sistem ini juga digambarkan, beserta contoh soal untuk konversi koordinat.

2. PENGERTIAN SISTEM KOORDINAT
Sistem koordinat adalah suatu cara/metode
untuk menentukan letak suatu titik dalam
grafik.
Ada beberapa macam system koordinat:
Sistem Koordinat Cartesius, Sistem
Koordinat Kutub.

3. ※ KOORDINAT KARTESIUS
Sistem koordinat kartesius digunakan untuk
menentukan tiap titik dalam bidang dengan
menggunakan dua bilangan yang biasa disebut
koordinat x dan koordinat y dari titik
tersebut.
Untuk mendeskripsikan suatu titik tertentu
dalam sistem koordinat dua dimensi, nilai x
ditulis (absis), lalu diikuti dengan nilai y
(ordinat). Dengan demikian, format yang
dipakai selalu (x,y) dan urutannya tidak
dibalik-balik.

4. ※ KOORDINAT KARTESIUS
 KOORDINAT KARTESIUS
x
A (x,y)
Suatu titik A dapat dinyatakan
sebagai pasangan berurut A(x,y)
y
X : jarak titik A terhadap sumbu -Y
y : jarak titik A terhadap sumbu -X
o
Ingat !
!
(X– , y+)
o
(X+ , y+)
(X– , y–) (X+ , y–)

5. Sistem koordinat Kartesius di
bawahTerdapat empat titik yang ditandai:
(2,3) titik hijau,
(-3,1) titik merah, (-1.5,-2.5) titik biru, dan
(0,0), titik asal, yang berwarna ungu.

6. •Sistem Koordinat kartesian 3 Dimensi
Sistem koordinat kartesian 3 dimensi yang berpusat di
O dan memiliki sumbu x, y dan z.

7. ※ KOORDINAT KUTUB
O (the pole)
ray (polar axis)
•Dalam beberapa hal, lebih mudah mencari lokasi/posisi
suatu titik dengan menggunakan koordinat polar.
•Koordinat polar menunjukkan posisi relatif terhadap
titik kutub O dan sumbu polar (ray) yang diberikan dan
berpangkal pada O.

8. ※ KOORDINAT KUTUB
 KOORDINAT KUTUB
A (r,
r
α)
Suatu titik A dapat dinyatakan sebagai
pasangan berurut A(r,α)
r : jarak titik A terhadap titik asal O (0,0)
o
α
Ingat !
!
Besar sudut di
berbagai kuadran
α : besar sudut antara sb-X (x positif)
terhadap garis OA
(r , ∠ K2)
(r , ∠
K3)
o
(r , ∠ K1)
(r , ∠
K4)

9. ※ KOORDINAT KARTESIUS &
KOORDINAT KUTUB
Hubungan Koordinat Kartesius & Koordinat Kutub :
A
r
o
α
x
Cos α = x
r
Sin α =
y
r
Ingat Letak
kuadran…
y
1. Jika diketahui Koordinat
Kutub ( r , α ) :
Maka :
x = r. cos α
y = r. sin α
2. Jika diketahui Koordinat
Kartesius ( x , y ) :
Maka : r =
tan α =
x2 + y2
y
x

10.  Contoh Soal :
Diketahui Koordinat Kutub :
A (r,
Ubahlah ke Koordinat Kartesius :
α)
Titik A ( 8,600 )
8
o
Maka :
x = r. cos α
600
y = r. sin α
 Jawab :
Titik A ( 8,600 )
⇒ x = r. cos α
y = r. sin α
= 8. sin 600
= 8 . cos 600
=8.
x=4
Jadi A ( 8,600 )
= 8.
1
2
⇔
1
2
y = 4√3
A ( 4, 4√3 )
3

11.  Contoh Soal :
Diketahui Koordinat Kutub :
B
Titik A ( 12 , 1500 )
(r, α )
Maka :
12
x = r. cos α
y = r. sin α
1500
o
Titik A ( 12, 1500 )
 Jawab :
y = r. sin α
⇒ x = r. cos α
= 12 . cos 1500
= 12. sin 1500
= 12 . – cos 300
= 12. sin 300
= 12 . −
x = – 6√3
Jadi B ( 12,1500 )
1
2
3
⇔
= 12.
y=6
B (– 6√3, 6 )
1
2

12.  Contoh Soal :
Diketahui Koordinat Kartesius :
4
A
r
(x,y)
Ubahlah ke Koordinat Kutub :
Titik A ( 4, 4√3 )
4√3
Maka :
o
r=
tan α =
x2 + y2
y
x
 Jawab :
Titik A (4, 4√3 )
⇒ r=
r = 16 + 48
4 2 + ( 4 3 )2
r = 64
r=8
Jadi A( 4, 4√3 )
⇔
tan α =
tan α =
y
x
4 3
4
tan α = √3
α = 600
A ( 8,600)

13.  Contoh Soal :
Diketahui Koordinat Kartesius :
Titik A ( 4, – 4)
4
o
Maka :
r=
-4
A
−4
4
tan α =
(x,y)
x2 + y2
y
x
42 + 42
 Jawab :
Titik A (4, – 4)
⇒ r=
r=
tan α =
32
r= 4 2
Jadi A( 4, – 4 )
⇔
y
x
tan α =
tan α = – 1
α = 3150
A ( 4 2 , 3150)

14. ※ Yang Perlu diingat :
(r , ∠ K1)
(r , ∠ K2)
B
A
r
r
C
Koordinat
Kartesius
(r , ∠
K3)
∠ K1
I. A (X+ , y+)
⇒
(r , ∠
K1)
II. B (X– , y+)
r
o
Koordinat
Kutub
⇒
(r , ∠
K2)
III. C (X – , y – )
⇒
(r , ∠
K3)
IV. D(X+ , y –)
⇒
(r , ∠
K4)
r
(r , ∠
K4)
D
Ingat
2x
Lho…

15. ※
A
r
r
C
Koordinat
Kartesius
(r , ∠ K1)
(r , ∠ K2)
B
Perhatikan contoh berikut :
(r , ∠
K3)
∠ K1
I. A (4 , 4)
⇒
(4√2 , 450)
II. B (-4 , 4)
r
o
Koordinat
Kutub
⇒
(4√2 ,1350)
III. C (-4 , -4 )
⇒
(4√2 , 2250)
IV. D(4 , -4)
⇒
(4√2 , 3150)
r
(r , ∠
K4)
D
Coba, Amati perbedaan
sudutnya……

16. ※ Soal Latihan :
1. Nyatakan koordinat kartesius dalam koordinat kutub :
a. ( – 5, – 5 )
b. ( 2, 3 )
2. Nyatakan koordinat kartesius dalam koordinat kutub :
a.( 8, 300 )
b.( 2, 1200 )
Kerjakan secara Teliti ….

17. WASSALAMUALAIKUM
Wr Wb