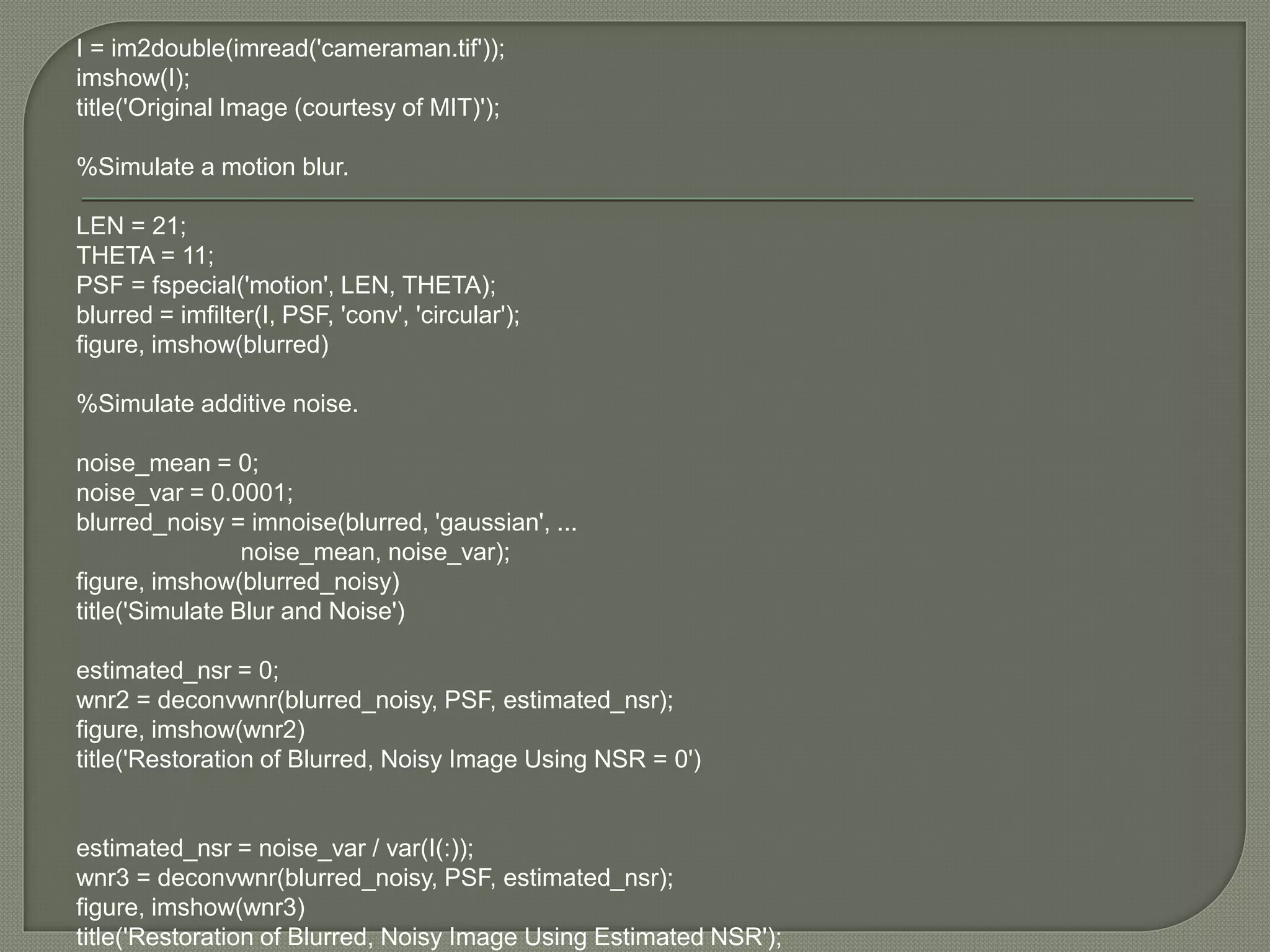
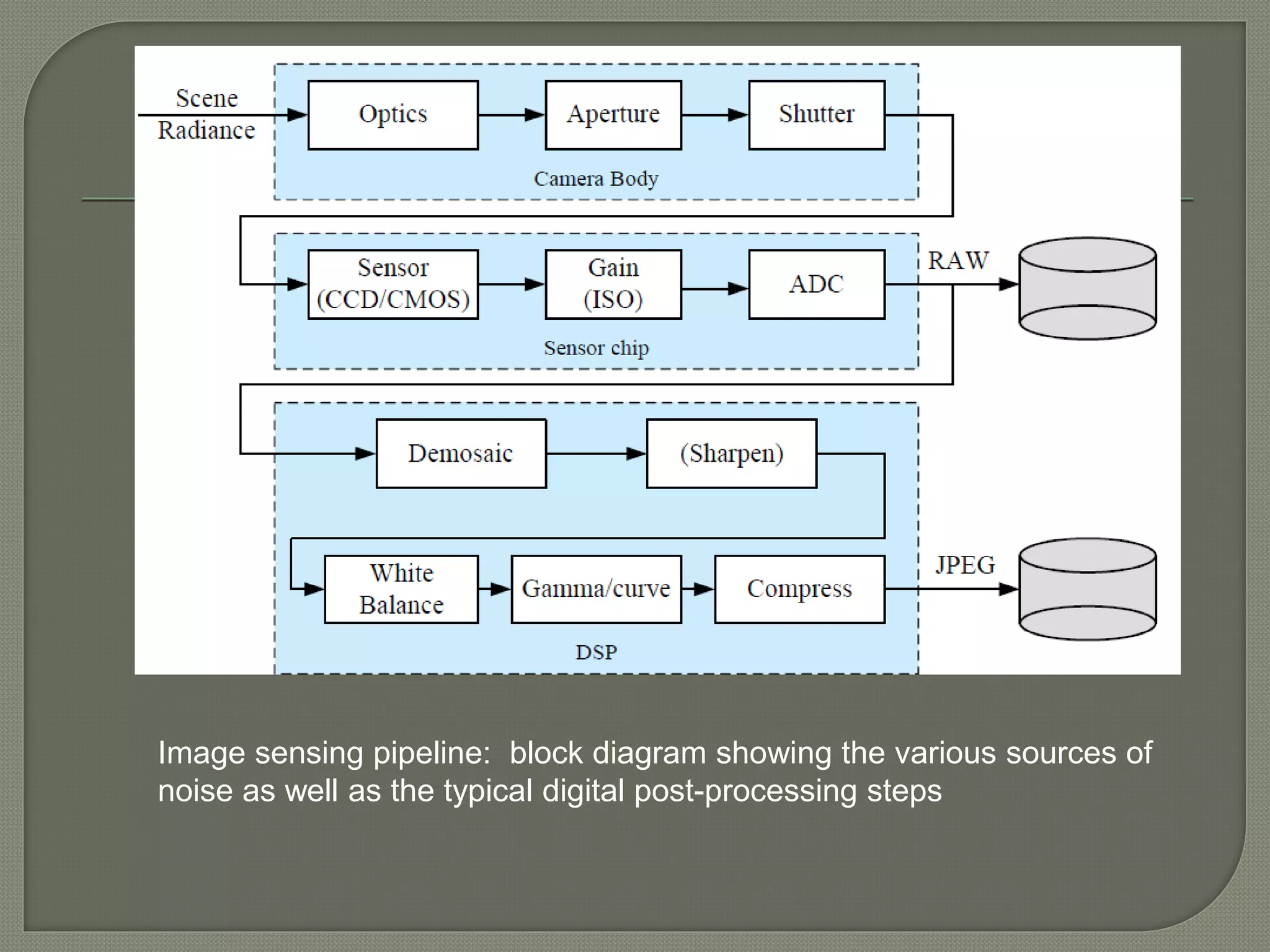
The document discusses various factors that affect the mapping of light intensity arriving at a camera lens to digital pixel values stored in an image file. It describes the radiometric response function, vignetting, and point spread function, which characterize how light is mapped and degraded by the camera imaging system. Sources of noise during image sensing and processing steps are also outlined. Methods to model and remove vignetting effects as well as deconvolve blur and noise in images using estimated point spread functions and noise levels are presented.

1. Ali Abdul-Zahraa
alia.alshamerty@student.uokufa.edu.iq

2. Before we can successfully merge multiple
photographs, we need to characterize the
functions that map incoming irradiance into
pixel values and also the amounts of noise
present each image.

3. Radiometric response function
Vignetting
point spread function

4. Image sensing pipeline: block diagram showing the various sources of
noise as well as the typical digital post-processing steps

5. which maps photons arriving at the lens
into digital values stored in the image file.
a number of factors affect how the intensity
of light arriving at the lens ends up being
mapped into stored digital values.

6. aperture and shutter speed:
 The shutter speed : directly controls the amount of light
reaching the sensor.
 (For bright scenes, where a large aperture or slow
shutter speed are desired to get a shallow depth of field
or motion blur, neutral density filters are sometimes
used by photographers.
 For dynamic scenes, the shutter speed also
determines the amount of motion blur in the resulting
picture.
 Usually, a higher shutter speed (less motion blur)

7. The analog to digital (A/D) converter
 on the sensing chip applies an electronic gain,
usually controlled by the ISO setting on your
camera.

8. Shutter and aperture are controls for
adjusting how much light comes into the
camera.
How much light is needed is determined by
the sensitivity of the medium used.
 That was as true for glass plates as it is
for film and now digital sensors. Over the
years that sensitivity has been expressed
in various ways, most recently as ASA and
now ISO.

9.  If you don't have a lot of light, or need a
fast shutter speed, you would probably
raise the ISO.
For dynamic scenes you need more ISO
value to treat shutter speed

10. Finally, a standard gamma is applied to the
intensities in each color channel and the
colors are converted into YCbCr format
before being transformed by a DCT,
quantized, and then compressed into the
JPEG format
where k is the coefficient (frequency) index

11. In this, there is no sub-sampling of the
chroma components, and can be as well
referred and used directly as a RGB
image.
High-end scanners / cameras / capture
devices use this format to not lose any
data.

12. Image sensing pipeline: block diagram showing the various sources of
noise as well as the typical digital post-processing steps

14. In addition to knowing the camera
response function, it is also often important
to know the amount of noise being injected
under a particular camera setting.
The simplest characterization of noise is a
single standard deviation, usually
measured in gray levels, independent of
pixel value.

16. %Read in an image. Because the image is a truecolor image, the
example converts it to grayscale.
RGB = imread('saturn.png');
I = rgb2gray(RGB);
%The example then add Gaussian noise to the image and then
displays the image.
J = imnoise(I,'gaussian',0,0.025);
imshow(J)
%Remove the noise, using the wiener2 function. Again, the figure only
shows a portion of the image
K = wiener2(J,[5 5]);
figure, imshow(K)

17.  In photography and optics, vignetting is a
reduction of an image's brightness or
saturation at the periphery compared to the
image center.
 A common problem with using wide-angle
and wide-aperture lenses is that the image
tends to darken in the corners
 This problem is generally known as
vignetting and comes in several different
forms, including natural, optical, and
mechanical vignetting

19. Mechanical vignetting
• occurs when light beams emanating from object
points located off-axis are partially blocked by
external objects such as thick or stacked filters,
secondary lenses, and improper lens hoods.

20. Optical vignetting
• This type of vignetting is caused by the physical
dimensions of a multiple element lens.
• Rear elements are shaded by elements in front of
them, which reduces the effective lens opening for
off-axis incident light.
• The result is a gradual decrease in light intensity
towards the image periphery.

21. Natural vignetting
• brightness depends on theta - angle between
surface normal (N) and the direction to the light
source (L)
I = Ip Kd cos(Ɵ) or I = Ip Kd (N' * L')

22. Post-shoot
• For artistic effect, vignetting is sometimes applied
to an otherwise un-vignetted photograph and can
be achieved by burning the outer edges of the
photograph or using digital imaging techniques,
such as masking darkened edges

24. img=imread('v2.jpg');
av=mean(img(:));
[m,n]=size(img)
subplot(1,2,1)
imshow(img)
for i=1:m
for j=1:n
if (av-img(i,j))<(av/2)
img(i,j)=img(i,j)+(av/2);
end
end
end
subplot(1,2,2)
imshow(img)

25. Also if we want to remove it , we can
compute overall brightness and compute
average of it and then increase low pixels
values compared with average to remove
low values .

26.  Most lenses including the human lens are not
perfect optical systems.
 As a result when visual stimuli are passed
through the cornea and lens the stimuli
undergo a certain degree of degradation.
 The question is how can this degradation be
represented? Well suppose you have an
exceedingly small dot of light, a point, and
project it through a lens. The image of this
point will not be the same as the original. The
lens will introduce a small amount of blur.
 point spread function (PSF)

27. I = imread('peppers.png');
I = I(60+[1:256],222+[1:256],:); % crop the image
figure; imshow(I); title('Original Image');
LEN = 31;
THETA = 11;
PSF = fspecial('motion',LEN,THETA); % create PSF
Blurred = imfilter(I,PSF,'circular','conv');
figure; imshow(Blurred); title('Blurred Image');
% Load image
I = im2double(Blurred);
figure(4); imshow(I); title('Source image');
%PSF
PSF = fspecial('motion', 14, 0);
noise_mean = 0;
noise_var = 0.0001;
estimated_nsr = noise_var / var(I(:));
I = edgetaper(I, PSF);
figure(5); imshow(deconvwnr(I, PSF, estimated_nsr)); title('Result')

28. I = im2double(imread('cameraman.tif'));
imshow(I);
title('Original Image (courtesy of MIT)');
%Simulate a motion blur.
LEN = 21;
THETA = 11;
PSF = fspecial('motion', LEN, THETA);
blurred = imfilter(I, PSF, 'conv', 'circular');
figure, imshow(blurred)
%Simulate additive noise.
noise_mean = 0;
noise_var = 0.0001;
blurred_noisy = imnoise(blurred, 'gaussian', ...
noise_mean, noise_var);
figure, imshow(blurred_noisy)
title('Simulate Blur and Noise')
estimated_nsr = 0;
wnr2 = deconvwnr(blurred_noisy, PSF, estimated_nsr);
figure, imshow(wnr2)
title('Restoration of Blurred, Noisy Image Using NSR = 0')
estimated_nsr = noise_var / var(I(:));
wnr3 = deconvwnr(blurred_noisy, PSF, estimated_nsr);
figure, imshow(wnr3)
title('Restoration of Blurred, Noisy Image Using Estimated NSR');