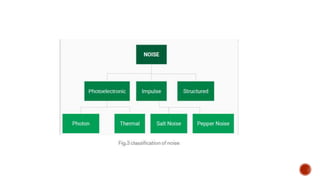
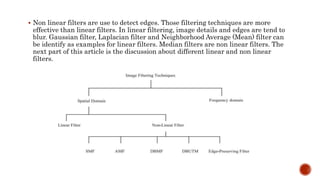
Digital image processing techniques can be used to enhance images by modifying pixel values using filters. Filters are classified as either spatial or frequency domain filters, with non-linear filters being more effective at edge detection than linear filters. The median filter is a common non-linear filter that replaces pixel values with the median of neighboring pixels to reduce salt-and-pepper noise. Image restoration techniques aim to reduce noise and recover lost resolution, such as by using deconvolution in the frequency domain to undo the effects of blurring.

1. Digital image processing
By.,
V.S. Priyadharshini –II-Msc(cs)

2.  Filtering techniques are use to enhance and modify digital images. Also, images
filters are use to blurring and noise reduction , sharpening and edge detection.
Image filters are mainly use for suppress high (smoothing techniques) and low
frequencies(image enhancement, edge detection). Classification of image filters.
 According to this classification, image filters can be divide in to two main
categories. Spatial filtering is the traditional method of image filtering. it is use
directly on the image pixels. Frequency domain filters are use to remove high and
low frequencies and smoothing.

3.  Non linear filters are use to detect edges. Those filtering techniques are more
effective than linear filters. In linear filtering, image details and edges are tend to
blur. Gaussian filter, Laplacian filter and Neighborhood Average (Mean) filter can
be identify as examples for linear filters. Median filters are non linear filters. The
next part of this article is the discussion about different linear and non linear
filters.

4.  Median filter is a non-linear filter. It replaces each pixel values by the median
values of it’s neighbor pixels. This is the efficient way for remove salt-and-pepper
noise. The calculation of the median value

5.  The Wiener filter is the MSE-optimal stationary linear filter for images degraded
by additive noise and blurring. Calculation of the Wiener filter requires the
assumption that the signal and noise processes are second-order stationary (in the
random process sense).
 Wiener filters are usually applied in the frequency domain. Given a degraded
image x(n,m), one takes the Discrete Fourier Transform (DFT) to obtain X(u,v).
The original image spectrum is estimated by taking the product of X(u,v) with the
Wiener filter G(u,v):


6.  Image restoration is performed by reversing the process that blurred the
image and such is performed by imaging a point source and use the point source
image, which is called the Point Spread Function (PSF) to restore the image
information lost to the blurring process.
 Image restoration is different from image enhancement in that the latter is
designed to emphasize features of the image that make the image more pleasing
to the observer, but not necessarily to produce realistic data from a scientific point
of view. Image enhancement techniques (like contrast stretching or de-blurring by
a nearest neighbor procedure) provided by imaging packages use no a priori model
of the process that created the image.

7.  With image enhancement noise can effectively be removed by sacrificing some
resolution, but this is not acceptable in many applications. In a fluorescence
microscope, resolution in the z-direction is bad as it is. More advanced image
processing techniques must be applied to recover the object.
 The objective of image restoration techniques is to reduce noise and recover
resolution loss. Image processing techniques are performed either in the image
domain or the frequency domain. The most straightforward and a conventional
technique for image restoration is deconvolution, which is performed in the
frequency domain and after computing the Fourier transform of both the image
and the PSF and undo the resolution loss caused by the blurring factors.

8.  This deconvolution technique, because of its direct inversion of the PSF which
typically has poor matrix condition number, amplifies noise and creates an
imperfect deblurred image. Also, conventionally the blurring process is assumed to
be shift-invariant. Hence more sophisticated techniques, such as regularized
deblurring, have been developed to offer robust recovery under different types of
noises and blurring functions.
 It is of 3 types:
1. Geometric correction
2. radiometric correction
3. noise removal

9.  Noise is always presents in digital images during image acquisition, coding,
transmission, and processing steps. It is very difficult to remove noise from the
digital images without the prior knowledge of filtering techniques.
 In this tutorial, we together will get a brief overview of various noise and the
filtering techniques of the same is described. These filters can be selected by
analysis of the noise behaviour. In this way, a complete and quantitative analysis
of noise and their best suited filters will be presented over here.

10.  Before going into Image processing let’s talk about image itself. Many of us think
of an image as a picture that we see in a wall or magazine etc.

11.  A(x,y) = H(x,y) + B(x,y) Where, A(x,y)= function of noisy image, H(x,y)= function of
image noise , B(x,y)= function of original image.But in theoretical terms, a picture
that we look at is a function of image intensity at a particular position in the
image. I.e I(x,y) is an image function where I = Intensity at position (x,y) in an
image.
 Types of digital images:
 There are typically three types of digital images.
Binary Images
Gray Scale Images
Color Images
 So, it can be stated as, f: [a,b] * [c,d] -> [min,max]

12.  While image being sent electronically from one place to another.
 Sensor heat while clicking an image.
 With varying ISO Factor which varies with the capacity of camera to absorb light.
 Types of Image noise:
There are different types of image noise. They can typically be divided into 3
types.