Download to read offline
Uploaded byAli A Jalil
Markov model
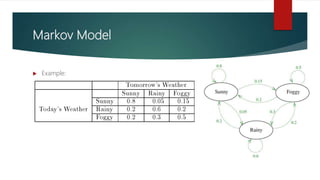
This document provides an introduction to Markov models and hidden Markov models. It explains that Markov models make the assumption that the probability of future states depends only on the present state, not on the sequence of events that preceded it. This allows weather prediction to be modeled based on the probability of today's weather given only yesterday's weather. Hidden Markov models add the complexity that the true states are hidden and can only be inferred from observable events, like whether an umbrella was carried based on the actual sunny, rainy, or foggy weather. The document gives examples of calculating state probabilities using these types of models.
More Related Content
Markov model
- 1. Markov Models ALI A.JALIL
- 2. Introduction Weather predictionis all about trying to guess what the weather will be like tomorrow based on a history of observations of weather Let us assume a simplified model of weather prediction we’ll collect statistics on what the weather was like today based on what the weather was like yesterday the day before and so forth We want to collect the following probabilities:
- 3. Introduction Using aboveexpression we can give probabilities of types of weather for tomorrow and the next day using n days of history For example if we knew that the weather for the past three days was (sunny, sunny foggy) in chronological order the probability that tomorrow would be rainy is given by: Here is the problem, the larger n is the more statistics we must collect, Suppose that n=5 then we must collect statistics for 243 past histories
- 4. Markov Models Thereforewe will make a simplifying assumption called the Markov Assumption: This is called a first order Markov assumption since we say that the probability of an observation at time n only depends on the observation at time n-1 A second order Markov assumption would have the observation at time n depend on n-1 and n-2.
- 5. Markov Models Wecan the express the joint probability using the Markov assumption: So this now has a profound affect on the number of histories that we have to find statistics for. we now only need 32 =9 numbers to characterize the probabilities of all of the sequences.
- 6.
- 7. Markov Model –Example Q: Given that today is sunny what is the probability that tomorrow is sunny and the day after is rainy?, A: Well this translates into:
- 8. Markov Model –Example Q: Given that today is foggy what is the probability that it will be rainy two days from now? A: There are three ways to get from foggy today to rainy two days from now (foggy, foggy, rainy), (foggy, rainy, rainy) and (foggy, sunny, rainy) Therefore we have to sum over these paths
- 9. Hidden Markov Model Well suppose you were locked in a room for several days and you were asked about the weather outside The only piece of evidence you have is whether the person who comes into the room carrying your daily meal is carrying an umbrella or not Let’s suppose the probabilities that your caretaker carries an umbrella is 0.1 if the weather is sunny, 0.8 if it is actually raining, and 0.3 if it is foggy.
- 10. Hidden Markov Model The equation for the weather Markov process before you were locked in the room was: However, the actual weather is hidden from you. Finding the probability of a certain weather qi ∈ {Sunny ,foggy, Cloudy } can only be based on the observation xi, with xi= ☂️ , if your caretaker brought an umbrella on day i and xi = 🌂 if the caretaker did not bring an umbrella.
- 11. Hidden Markov Model This conditional probability P(qi|xi) can be rewritten according to Bayes’ rule: or, for n days, and weather sequence Q = {q1, . . . , qn}, as well as ‘umbrella sequence’ X = {x1, , . . . , xn} using the probability P(q1, . . . , qn) of a Markov weather sequence from above, and the probability P(x1, . . . , xn) of seeing a particular sequence of umbrella events (e.g., {☂️ , 🌂 , ☂️ }). The probability P(x1, . . . ,xn|q1,.. .,qn) can be estimated as if you assume that, for all i, the qi, xi are independent of all xj and qj , for all j ≠ i.
- 12. Hidden Markov Model We want to draw conclusions from our observations (if the persons carries an umbrella or not) about the weather outside.
- 13. Hidden Markov Model- Example Q: Suppose the day you were locked in it was sunny. The next day, the caretaker carried an umbrella into the room. You would like to know, what the weather was like on this second day. A: First we calculate the likelihood for the second day to be sunny: p(q2 =Sunny|q1 = Sunny, x2 = ☂️) = p(x2 = ☂️ |q2 =Sunny ) * P(q2 = Sunny|q1 =Sunny ) = 0.1* 0.8 = 0.08 then for the second day to be rainy: p(q2 =rainy|q1 =sunny, x2 = ☂️) = P(x2 = ☂️ |q2 = rainy) * P(q2 = ☂️ |q1 =sunny)= 0.8 * 0.05 = 0.04 and finally for the second day to be foggy: p(q2 = |q1 = , x2 = ) = P(x2 = |q2 = ) * P(q2 = |q1 = )= 0.3 *0.15 = 0.045 Thus, although the caretaker did carry an umbrella, it is most likely that on the second day the weather was sunny.
- 14.