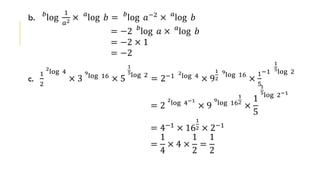Dokumen ini menjelaskan logaritma, yang pertama kali diperkenalkan oleh John Napier, serta penggunaannya dalam perhitungan matematikal yang kompleks, termasuk pertumbuhan dan peluruhan. Berbagai sifat logaritma dijelaskan, disertai dengan contoh persamaan dan penyelesaiannya. Selain itu, cara menentukan himpunan penyelesaian dari persamaan logaritma juga diuraikan dengan contoh-contoh yang mendetail.

1. LOGARITMA

2. MOTIVASI
Logaritma diperkenalkan pertama kali oleh John Napier
(matematikawan Skotlandia). Napier menemukan sebuah sistem yang
dikenal “Napierian Logarithm”. Sistem ini digunakan untuk perhitungan
yang kompleks, tidak hanya melibatkan penjumlahan, pengurangan,
perkalian dan pembagian, tetapi juga perpangkatan dan fungsi
trigonometri.
Banyak sekali masalah dalam ilmu pengetahuan, teknologi maupun
dalam kehidupan sehari-hari yang melibatkan fungsi atau persamaan
logaritma, terutama peristiwa pertumbuhan dan peluruhan. Hal ini
dikarenakan logaritma merupakan invers (kebalikan) dari eksponen.
Logartima juga digunakan untuk memecahkan masalah eksponen yang
sulit dicari akar-akar atau penyelesaiannya.

3. PERSAMAAN LOGARITMA
Logaritma merupakan invers (kebalikan) dari eksponen.
Bisa ditulis:
𝒂 𝒄 = 𝒃 ⟺ 𝒂
𝐥𝐨𝐠 𝒃 = 𝒄
Logaritma dari 𝑏 dengan bilangan pokok 𝑎 ditulis sebagai 𝑎
log 𝑏 dengan
𝑎 > 0, 𝑎 ≠ 1 dan 𝑏 ≥ 0 (b disebut numerus).
Suatu persamaan dengan numerus atau bilangan logaritmanya memuat
variabel 𝑥 disebut persamaan logaritma. Contoh persamaan logaritma.
 2
log 𝑥 𝑥 + 4 = 2
log 12
 3
log 𝑥 + 1 + 3
log 𝑥 + 2 = 9
log 4𝑥 + 4

4. SIFAT-SIFAT LOGARITMA
Sifat-sifat logaritma adalah sebagai beriku:
Misalkan 𝑞, 𝑎, 𝑏, 𝑛, 𝑝 > 0, 𝑞 ≠ 1 dan 𝑎 ≠ 1, 𝑝 ≠ 1:
A. i)
𝑞
log 1 = 0 ii)
𝑞
log 𝑞 = 1 iii)
𝑞
log 𝑞 𝑛 = 𝑛
B.
𝑞
log 𝑎𝑏 =
𝑞
log 𝑎 +
𝑞
log 𝑏
C.
𝑞
log
𝑎
𝑏
=
𝑞
log 𝑎 −
𝑞
log 𝑏
D.
𝑞
log 𝑎 𝑛 = 𝑛
𝑞
log 𝑎
E. 𝑎
log 𝑏 =
𝑝
log 𝑎
𝑝
log 𝑏
F. 𝑎
𝑎
log 𝑏
= 𝑏
G. 𝑎
log 𝑏 × 𝑏
log 𝑎 = 1
Catatan:
Logaritma dengan
bilangan pokok 10,
bilangan pokok
biasanya tidak
ditulis. Jadi, 10
log 𝑎
ditulis log 𝑎.

5. CONTOH1:
Sederhanakanlah bentuk logaritma berikut ini!
a. 3 3
log 5 + 2 3
log 2
b.
1
3
5
log 27 + 5
log 3 −
2
3
5
log 3
Jawab:
a. 3 3
log 5 + 2 3
log 2 = 3
log 53 + 3
log 22
= 3
log 125 + 3
log 4
= 3
log 500

6. b.
1
3
5
log 27 + 5
log 3 −
2
3
5
log 3 = 5
log 27
1
3 + 5
log 3 − 5
log 3
2
3
= 5
log 33
1
3 + 5
log 3 − 5
log 3
2
3
= 5
log 3 + 5
log
3
3
2
3
= 5
log 3 + 5
log 3
1
3
= 5
log 3 . 3
1
3
= 5
log 3
4
3
= 5
log
3
81
= 5
log 3
3
3

7. CONTOH2:
Tentukan nilai dari logaritma berikut ini!
a. 8
2
log 3
b. 𝑏
log
1
𝑎2 × 𝑎
log 𝑏
c.
1
2
2
log 4
× 3
9
log 16
× 5
1
5log 2
Jawab:
a. 8
2
log 3
= 2 3 2
log 3
= 2
2
log 33
= 27

8. b. 𝑏
log
1
𝑎2 × 𝑎
log 𝑏 = 𝑏
log 𝑎−2 × 𝑎
log 𝑏
= −2 𝑏
log 𝑎 × 𝑎
log 𝑏
= −2 × 1
= −2
c.
1
2
2
log 4
× 3
9
log 16
× 5
1
5log 2
= 2−1 2
log 4
× 9
1
2
9
log 16
×
1
5
−1
1
5log 2
= 2
2
log 4−1
× 9
9
log 16
1
2
×
1
5
1
5log 2−1
= 4−1 × 16
1
2 × 2−1
=
1
4
× 4 ×
1
2
=
1
2

9. MENENTUKAN PENYELESAIAN PERSAMAAN LOGARITMA
Himpunan penyelesaian dari persamaan logaritma
𝑎
log 𝑓 𝑥 = 𝑎
log 𝑝 dengan 𝑎 > 0, 𝑎 ≠ 1, dapat ditentukan
dengan sifat berikut:
Jika 𝒑 > 𝟎 dan 𝒂
𝐥𝐨𝐠 𝒇 𝒙 = 𝒂
𝐥𝐨𝐠 𝒑, maka 𝒇 𝒙 = 𝒑 asalkan
𝒇 𝒙 > 𝟎

10. CONTOH:
Tentukan himpunan penyelesaian dari persamaan logaritma berikut!
a. log 2𝑥 − 3 − log 𝑥 − 3 = log 5
b. 3
log 𝑥 − 3 = 9
log 16
Jawab:
a. log 2𝑥 − 3 − log 𝑥 − 3 = log 5
(i) Numerus harus positif 𝑓 𝑥 > 0
 2𝑥 − 3 > 0 ⟺ 𝑥 >
3
2
 𝑥 − 3 > 0 ⟺ 𝑥 > 3
Syarat numerus yang harus dipenuhi adalah 𝑥 > 3

11. (ii) log 2𝑥 − 3 − log 𝑥 − 3 = log 5
log
2𝑥 − 3
𝑥 − 3
= log 5
2𝑥 − 3
𝑥 − 3
= 5
2𝑥 − 3 = 5𝑥 − 15
3𝑥 = 12
𝑥 = 4
Karena 𝑥 > 3, maka himpunan penyelesaiannya adalah {4}.

12. b. 3
log 𝑥 − 3 = 9
log 16
(i) Numerus harus positif 𝑓 𝑥 > 0
 𝑥 − 3 > 0 ⟺ 𝑥 > 3
Syarat numerus yang harus dipenuhi adalah 𝑥 > 3
(ii) 3
log 𝑥 − 3 = 9
log 16
⟺ 3
log 𝑥 − 3 =
3
log 16
3log 9
3
log 𝑥 − 3 =
3
log 16
2
2 3
log 𝑥 − 3 = 3
log 16
3
log 𝑥 − 3 2
= 3
log 16
𝑥 − 3 2
= 16
𝑥2
− 6𝑥 + 9 = 16
𝑥2 − 6𝑥 − 7 = 0
𝑥 − 7 𝑥 + 1 = 0
𝑥 = 7 atau 𝑥 = −1
Karena 𝑥 > 3, maka himpunan penyelesaiannya adalah {7}.

13. Himpunan penyelesaian dari persamaan logaritma
𝑎
log 𝑓 𝑥 = 𝑏
log 𝑓 𝑥 dengan 𝑎 > 0, 𝑎 ≠ 𝑏 serta 𝑓 𝑥 dan
𝑔 𝑥 fungsi aljabar, dapat ditentukan dengan sifat berikut:
Jika 𝒂
𝐥𝐨𝐠 𝒇 𝒙 = 𝒃
𝐥𝐨𝐠 𝒇 𝒙 , maka 𝒇 𝒙 = 𝟏 asalkan 𝒇 𝒙 >
𝟎, 𝒂 ≠ 𝒃

14. Himpunan penyelesaian dari persamaan logaritma
𝑎
log 𝑓 𝑥 = 𝑎
log 𝑔 𝑥 dengan 𝑎 > 0, 𝑎 ≠ 1 serta 𝑓 𝑥 dan
𝑔 𝑥 fungsi aljabar, dapat ditentukan dengan sifat berikut:
Jika 𝒂
𝐥𝐨𝐠 𝒇 𝒙 = 𝒂
𝐥𝐨𝐠 𝒈 𝒙 , maka 𝒇 𝒙 = 𝒈 𝒙 asalkan
𝒇 𝒙 > 𝟎, 𝒈 𝒙 > 𝟎

15. CONTOH:
Tentukan himpunan penyelesaian dari persamaan logaritma berikut!
a. 3
log 𝑥2 + 3𝑥 + 2 = 3
log 5𝑥 + 5
b. 2
log 2
log 𝑥 + 7 + 1 = 2
log 2
log 𝑥 + 2
log 𝑥 − 3
Jawab:
a. 3
log 𝑥2 + 3𝑥 + 2 = 3
log 5𝑥 + 5
(i) Numerus harus positif 𝑓 𝑥 > 0
 𝑥2 + 3𝑥 + 2 > 0 ⟺ 𝑥 + 2 𝑥 + 1 > 0
𝑥 < −2 atau 𝑥 > −1
 5𝑥 + 5 > 0 ⟺ 𝑥 > −1
Syarat numerus yang harus dipenuhi adalah 𝑥 > −1

16. (ii) 3
log 𝑥2
+ 3𝑥 + 2 = 3
log 5𝑥 + 5
⟺ 𝑥2 + 3𝑥 + 2 = 5𝑥 + 5
⟺ 𝑥2
− 2𝑥 − 3 = 0
⟺ 𝑥 − 3 𝑥 + 1 = 0
⟺ 𝑥 = 3 atau 𝑥 = −1
Karena 𝑥 > −1, maka himpunan penyelesaiannya adalah {3}.
b. Persamaan ini terdiri dari dua logaritma, jadi kita selesaikan satu
persatu.
2
log 2
log 𝑥 + 7 + 1 = 2
log 2
log 𝑥 + 2
log 𝑥 − 3
⟺ 2
log 2
log 𝑥 + 7 + 2
log 2 = 2
log 2
log 𝑥 𝑥 − 3
⟺ 2
log 2
log 2 𝑥 + 7 = 2
log 2
log 𝑥 𝑥 − 3

17. Dengan menghapus logaritma yang pertama, maka:
2
log 2𝑥 + 14 = 2
log 𝑥2 − 3𝑥
(i) Numerus harus positif 𝑓 𝑥 > 0
 2𝑥 + 14 > 0 ⟺ 𝑥 > −7
 𝑥2 − 3 > 0 ⟺ 𝑥 𝑥 − 3 > 0
⟺ 𝑥 < 0 atau 𝑥 > 3
Syarat numerus yang harus dipenuhi adalah 𝑥 > 3
(ii) 2
log 2𝑥 + 14 = 2
log 𝑥2
− 3𝑥
⟺ 2𝑥 + 14 = 𝑥2 − 3𝑥
⟺ 𝑥2 − 5𝑥 − 14 = 0
⟺ 𝑥 − 7 𝑥 + 2 = 0
⟺ 𝑥 = 7 atau 𝑥 = −2
Karena 𝑥 > 3, maka himpunan penyelesaiannya adalah {7}.

18. Himpunan penyelesaian dari persamaan logaritma
ℎ(𝑥)
log 𝑓 𝑥 =
ℎ(𝑥)
log 𝑔 𝑥 dengan 𝑓 𝑥 , 𝑔 𝑥 dan ℎ 𝑥
fungsi aljabar, dapat ditentukan dengan sifat berikut:
Jika
𝒉(𝒙)
𝐥𝐨𝐠 𝒇 𝒙 =
𝒉(𝒙)
𝐥𝐨𝐠 𝒈 𝒙 , maka 𝒇 𝒙 = 𝒈 𝒙 asalkan
𝒇 𝒙 > 𝟎, 𝒈 𝒙 > 𝟎, serta 𝒉 𝒙 > 𝟎 dan 𝒉 𝒙 ≠ 𝟏

19. CONTOH:
Tentukan himpunan penyelesaian dari persamaan logaritma berikut!
𝑥
log 𝑥 + 15 − 2 𝑥
log 10 + 1 = 0
Jawab:
𝑥
log 𝑥 + 15 − 2 𝑥
log 10 + 𝑥
log 𝑥 = 0
⟺ 𝑥
log 𝑥 + 15 + 𝑥
log 𝑥 = 2 𝑥
log 10
⟺ 𝑥
log 𝑥 𝑥 + 15 = 𝑥
log 102
⟺ 𝑥
log 𝑥2
+ 15𝑥 = 𝑥
log 100

20. (i) Numerus dan bilangan pokok
 ℎ(𝑥) > 0 dan ℎ 𝑥 ≠ 1 ⟺ 𝑥 > 0 dan 𝑥 ≠ 1
 𝑓 𝑥 > 0 ⟺ 𝑥2 + 15𝑥 > 0
𝑥 𝑥 + 15 > 0
𝑥 < −15 atau 𝑥 > 0
Syarat bilangan pokok dan numerus yang harus dipenuhi adalah 𝑥 > 0
dan 𝑥 ≠ 1.
(ii) 𝑥
log 𝑥2
+ 15𝑥 = 𝑥
log 100
⟺ 𝑥2
+ 15𝑥 = 100
⟺ 𝑥2 + 15𝑥 − 100 = 0
⟺ 𝑥 + 20 𝑥 − 5 = 0
⟺ 𝑥 = −20 atau 𝑥 = 5
Karena 𝑥 > 0 dan 𝑥 ≠ 1, maka himpunan penyelesaiannya adalah {5}.

21. Himpunan penyelesaian dari persamaan
logaritma 𝐴 𝑎
log 𝑓(𝑥) 2
+ 𝐵 𝑎
log 𝑓(𝑥) + 𝐶 = 0 dengan 𝑎 >
0, 𝑎 ≠ 1 serta 𝑓 𝑥 > 0, dapat ditentukan dengan mengubah
persamaan tersebut ke dalam bentuk persamaan kuadrat.

22. CONTOH:
Tentukan himpunan penyelesaian dari persamaan logaritma berikut!
2
log2 𝑥 − 2 2
log 𝑥2 = 5
Jawab:
2
log2 𝑥 − 2 2
log 𝑥2 = 5
⟺
2
log 𝑥 2
− 4 2
log 𝑥 − 5 = 0
⟺ 𝑝2
− 4𝑝 − 5 = 0
⟺ 𝑝 − 5 𝑝 + 1 = 0
⟺ 𝑝 = 5 atau 𝑝 = −1

23.  𝑝 = 5 ⟺ 2
log 𝑥 = 5
⟺ 𝑥 = 25
⟺ 𝑥 = 32
 𝑝 = −1 ⟺ 2
log 𝑥 = −1
⟺ 𝑥 = 2−1
⟺ 𝑥 =
1
2
Jadi, himpunan penyelesaian persamaan tersebut adalah
1
2
, 32