Download as PDF, PPTX
Uploaded byEman Mendrofa
Notasi sigma
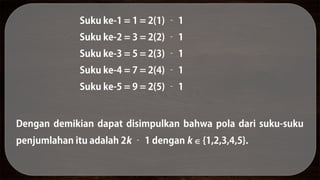
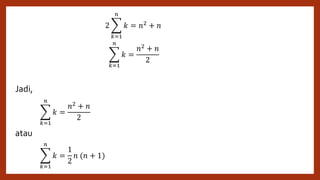
Dokumen ini menjelaskan metode yang digunakan Carl Friedrich Gauss untuk menghitung jumlah bilangan bulat dari 1 sampai 100 dengan cara cepat. Teknik ini melibatkan pemahaman tentang notasi sigma dan sifat-sifatnya yang memudahkan perhitungan jumlah suku. Selain itu, dokumen ini memberikan contoh-contoh perhitungan serta tugas yang melibatkan penggunaan notasi sigma.
More Related Content
![Modul Ajar KBC Fikih Kelas 8 MTs [MODULKELAS.COM]](https://cdn.slidesharecdn.com/ss_thumbnails/modulajarkbcfikihkelas8mtsmodulkelas-260122161545-045338bd-thumbnail.jpg?width=640&height=640&fit=bounds)
Notasi sigma
- 1.
- 2. Pengerjaan dengan singkatdiperkenalkan oleh Carl Friedrich Gauss, seorang matematikawan dari Jerman. Saat itu Gauss mendapat tugas dari gurunya untuk menghitung jumlah bilangan bulat dari 1 sampai 100. Pada mulanya gurunya yakin bahwa pengerjaannya membutuhkan waktu cukup lama. Akan tetapi gurunya terkejut ketika Gauss telah menemukan jawaban yang benar dan ditulis pada selembar kertas dengan waktu yang singkat.
- 3. Bagaimanakah Gauss menemukanjawaban tugas tersebut?? Gauss menggunakan skema berikut ini: 1 + 2 + 3 + . . . + 99 + 100 100 + 99 + 98 + . . . + 2 + 1 101 + 101 + 101 + . . . + 101 + 101 = 10.100 Kemudian Gauss menyimpulkan bahwa jumlah bilangan bulat dari 1 sampai 100 adalah 10.100 : 2 = 5.050. +
- 5.
- 6.
- 7. 𝒂 𝟏 𝒂 𝟐 𝒂𝒏 𝑘=1 𝑛 𝑎 𝑘 = 𝑎1 + 𝑎2 + 𝑎3+ . . . +𝑎 𝑛
- 8. 𝑘=1 4 2𝑘2 − 1 𝑘=1 4 2𝑘2− 1 = 2 . 12 − 1 + 2 . 22 − 1 + 2 . 32 − 1 + 2 . 42 − 1 = 1 + 7 + 17 + 31
- 9. 𝑘=1 4 2𝑘2 − 1= 2 . 12 − 1 + 2 . 22 − 1 + 2 . 32 − 1 + 2 . 42 − 1 = 1 + 7 + 17 + 31 = 56 𝑘=1 4 2𝑘2 − 1 = 56
- 11. 𝑘=1 6 2𝑘 + 12 = 32 + 52 + 72 + 92 + 112 + 132 𝑘=1 5 2𝑘 + 1 2 = 32 + 52 + 72 + 92 + 112 𝑘=1 6 2𝑘 + 1 2 = 𝑘=1 5 2𝑘 + 1 2 + 132
- 12. 𝒂 𝒏 𝒌=𝟏 𝒏 𝒂 𝒌= 𝒌=𝟏 𝒏−𝟏 𝒂 𝒌 + 𝒂 𝒏
- 13.
- 14.
- 15. 𝒌=𝟏 𝟖 (𝟓𝒌 − 𝟑) −− − − − − 𝒌=𝟏 𝟒 −𝟏 𝒌 𝒌 𝒌 + 𝟏
- 16. Bentuk penjumlahan yangdituliskan dengan notasi sigma memiliki beberapa kaidah-kaidah (sifat) tertentu. Jika C adalah suatu konstanta, maka: Sifat Pertama 𝒌=𝟏 𝒏 𝑪 = 𝒏𝑪
- 17. Bukti: Jadi, Dari sifat pertamaini diperoleh: 𝑘=1 𝑛 𝐶 = 𝐶 + 𝐶 + 𝐶+ . . . +𝐶 𝑘=1 𝑛 𝐶 = 𝑛𝐶 n buah 𝑘=1 𝑛 𝐶 = 𝑛𝐶 (terbukti) 𝑘=1 𝑛 1 = 𝑛
- 18. Jika 𝒂 𝒌merupakan suku ke-k dan C suatu konstanta, maka: Bukti: 𝒌=𝟏 𝒏 𝑪 𝒂 𝒌 = 𝑪 𝒌=𝟏 𝒏 𝒂 𝒌 Sifat Kedua 𝒌=𝟏 𝒏 𝑪 𝒂 𝒌 = 𝑪𝒂 𝟏 + 𝑪𝒂 𝟐 + 𝑪𝒂 𝟑+ . . . +𝑪𝒂 𝒏 = 𝑪 (𝒂 𝟏 + 𝒂 𝟐 + 𝒂 𝟑+ . . . +𝒂 𝒏) 𝒌=𝟏 𝒏 𝑪 𝒂 𝒌 = 𝑪 𝒌=𝟏 𝒏 𝒂 𝒌 (terbukti)
- 19. Jika 𝒂 𝒌dan 𝒃 𝒌 merupakan suku ke-k, maka: Bukti: 𝒌=𝟏 𝒏 (𝒂 𝒌 + 𝒃 𝒌) = 𝒌=𝟏 𝒏 𝒂 𝒌 + 𝒌=𝟏 𝒏 𝒃 𝒌 Sifat Ketiga 𝒌=𝟏 𝒏 (𝒂 𝒌 + 𝒃 𝒌) = (𝒂 𝟏 + 𝒃 𝟏) + (𝒂 𝟐 + 𝒃 𝟐) + (𝒂 𝟑 + 𝒃 𝟑)+ . . . +(𝒂 𝒏 + 𝒃 𝒏)
- 20. Jadi, (terbukti) 𝒌=𝟏 𝒏 (𝒂 𝒌 +𝒃 𝒌) = (𝒂 𝟏 + 𝒂 𝟐 + 𝒂 𝟑+ . . . + 𝒂 𝒏) + (𝒃 𝟏+𝒃 𝟐 + 𝒃 𝟑+ . . . + 𝒂 𝒏) 𝒌=𝟏 𝒏 𝒂 𝒌 + 𝒃 𝒌 = 𝒌=𝟏 𝒏 𝒂 𝒌 + 𝒌=𝟏 𝒏 𝒃 𝒌 𝒌=𝟏 𝒏 (𝒂 𝒌 + 𝒃 𝒌) = 𝒌=𝟏 𝒏 𝒂 𝒌 + 𝒌=𝟏 𝒏 𝒃 𝒌
- 21. Jika 𝒂 𝒌dan 𝒃 𝒌 merupakan suku ke-k, maka: Bukti: 𝒌=𝟏 𝒏 (𝒂 𝒌 + 𝒃 𝒌) 𝟐= 𝒌=𝟏 𝒏 (𝒂 𝒌) 𝟐 + 𝟐 𝒌=𝟏 𝒏 𝒂 𝒌 𝒃 𝒌 + 𝒌=𝟏 𝒏 (𝒃 𝒌) 𝟐 Sifat keempat 𝒌=𝟏 𝒏 (𝒂 𝒌 + 𝒃 𝒌) 𝟐 = 𝒌=𝟏 𝒏 (𝒂 𝒌 𝟐 + 𝟐 𝒂 𝒌 𝒃 𝒌 + 𝒃 𝒌 𝟐 )
- 22. Jadi 𝒌=𝟏 𝒏 (𝒂 𝒌 +𝒃 𝒌) 𝟐 = 𝒌=𝟏 𝒏 𝒂 𝒌 𝟐 + 𝒌=𝟏 𝒏 𝟐 𝒂 𝒌 𝒃 𝒌 + 𝒌=𝟏 𝒏 𝒃 𝒌 𝟐 𝒌=𝟏 𝒏 (𝒂 𝒌 + 𝒃 𝒌) 𝟐 = 𝒌=𝟏 𝒏 𝒂 𝒌 𝟐 + 𝟐 𝒌=𝟏 𝒏 𝒂 𝒌 𝒃 𝒌 + 𝒌=𝟏 𝒏 𝒃 𝒌 𝟐 𝒌=𝟏 𝒏 (𝒂 𝒌 + 𝒃 𝒌) 𝟐= 𝒌=𝟏 𝒏 (𝒂 𝒌) 𝟐 + 𝟐 𝒌=𝟏 𝒏 𝒂 𝒌 𝒃 𝒌 + 𝒌=𝟏 𝒏 (𝒃 𝒌) 𝟐 (terbukti)
- 23. Hasil penjumlahan dengannotasi sigma dapat dihitung dengan cepat apabila banyak sukunya (n) sedikit, tetapi jika banyak sukunya (n) besar maka perlu menggunakan rumus tertentu. Menentukan nilai Kita tahu bahwa: 𝑘=1 𝑛 𝑘 𝑘2 + 2𝑘 + 1 = (𝑘 + 1)2 2𝑘 + 1 = (𝑘 + 1)2 − 𝑘2
- 24. Sehingga untuk: 𝑘 =1, maka 2𝑘 + 1 bernilai 22 − 12 𝑘 = 2, maka 2𝑘 + 1 bernilai 32 − 12 𝑘 = 3, maka 2𝑘 + 1 bernilai 42 − 12 𝑘 = 𝑛 − 1, maka 2𝑘 + 1 bernilai 𝑛2 − (𝑛 − 1)2 𝑘 = 𝑛, maka 2𝑘 + 1 bernilai (𝑛 + 1)2−𝑛2 + 𝑘=1 𝑛 2𝑘 + 1 = (𝑛 + 1)2−12 = 𝑛2 + 2𝑛 + 1 − 1 = 𝑛2 + 2𝑛
- 25. Berdasarkan kaidah-kaidah notasisigma, didapat: Dari uraian di atas, maka diperoleh persamaan: 𝑘=1 𝑛 2𝑘 + 1 = 𝑘=1 𝑛 2𝑘 + 𝑘=1 𝑛 1 = 2 𝑘=1 𝑛 𝑘 + 𝑛 2 𝑘=1 𝑛 𝑘 + 𝑛 = 𝑛2 + 2𝑛 2 𝑘=1 𝑛 𝑘 = 𝑛2 + 2𝑛 − 𝑛
- 26. Jadi, atau 2 𝑘=1 𝑛 𝑘 = 𝑛2 +𝑛 𝑘=1 𝑛 𝑘 = 𝑛2 + 𝑛 2 𝑘=1 𝑛 𝑘 = 𝑛2 + 𝑛 2 𝑘=1 𝑛 𝑘 = 1 2 𝑛 (𝑛 + 1)
- 27. Contoh1: Hitunglah 3 +6 + 9 + 12 + . . . + 45 Jawab: 3 + 6 + 9 + 12 + . . . + 45 = 3 (1 + 2 + 3 + . . . + 15) = 3 𝑘=1 15 𝑘 = 3 152 + 15 2 = 360
- 28. Contoh2: Hitunglah 5 +7 + 9 + 11 + 13+ . . . + 23 Jawab: 5 + 7 + 9 + 11 + 13+ . . . + 23 = (2(1) + 3) + (2(2) + 3) + (2(3) + 3) + . . . + (2(10) + 3) = 𝑘=1 10 (2𝑘 + 3) = 2 102 + 10 2 + 30 = 140 = 𝑘=1 10 2𝑘 + 𝑘=1 10 3 = 2 𝑘=1 10 𝑘 + (3 . 10)
- 29. Tugas 1. Tulislah denganmenggunakan notasi sigma. a. 2 + 4 + 8 + 16 + 32 + 64 b. 1 2 + 1 3 + 1 4 + . . . + 1 100 2. Nyatakan dalam bentuk penjumlahan. 𝑛=0 7 (2 − 𝑛) 𝑘=2 𝑛 𝑘(𝑘 + 1) 2 a. b.
- 30. 3. Diketahui: 𝑎1= 2, 𝑎2 = 3, 𝑎3 = 5, 𝑎4 = 7, 𝑎5 = 11, 𝑎6 = 13 𝑏1 = −3, 𝑏2 = −2, 𝑏3 = 0, 𝑏4 = 1, 𝑏5 = 2, 𝑏6 = −1 Hitunglah: 𝑘=1 6 (𝑎 𝑘 + 𝑏 𝑘)2 𝑘=1 6 (𝑎 𝑘 + 𝑏 𝑘)(𝑎 𝑘 − 𝑏 𝑘) a. b.