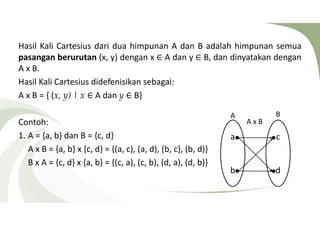
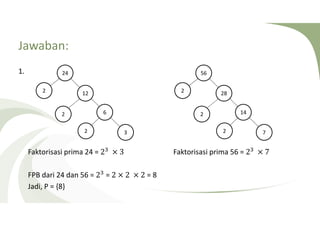
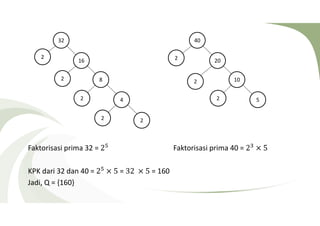
Dokumen tersebut membahas tentang relasi dan hasil kali cartesius antara dua himpunan atau lebih. Definisi relasi adalah pernyataan yang mendefinisikan hubungan antara suatu himpunan dengan himpunan lainnya. Hasil kali cartesius dari dua himpunan adalah himpunan semua pasangan berurutan dengan elemen pertama dari himpunan pertama dan elemen kedua dari himpunan kedua.