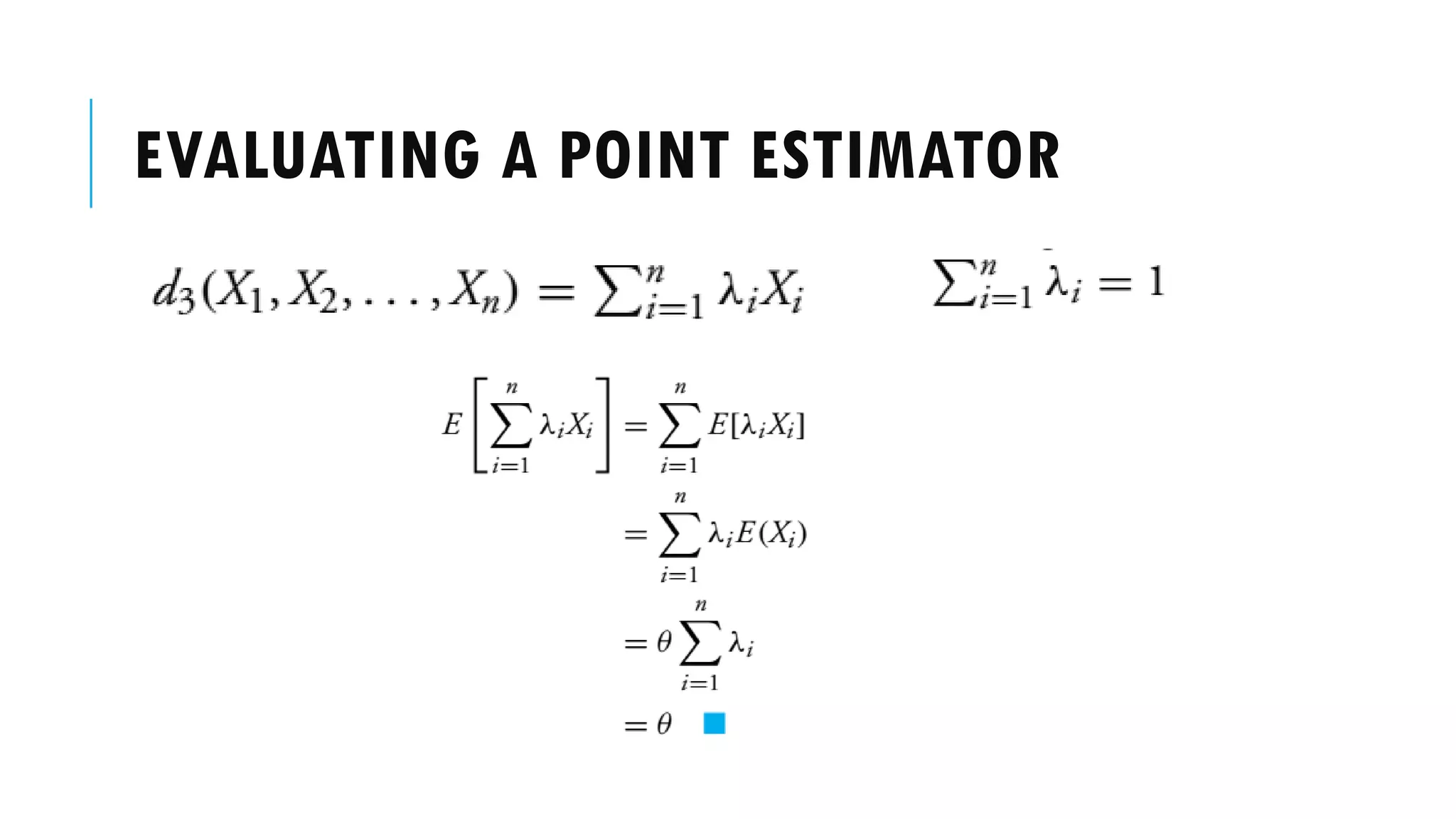
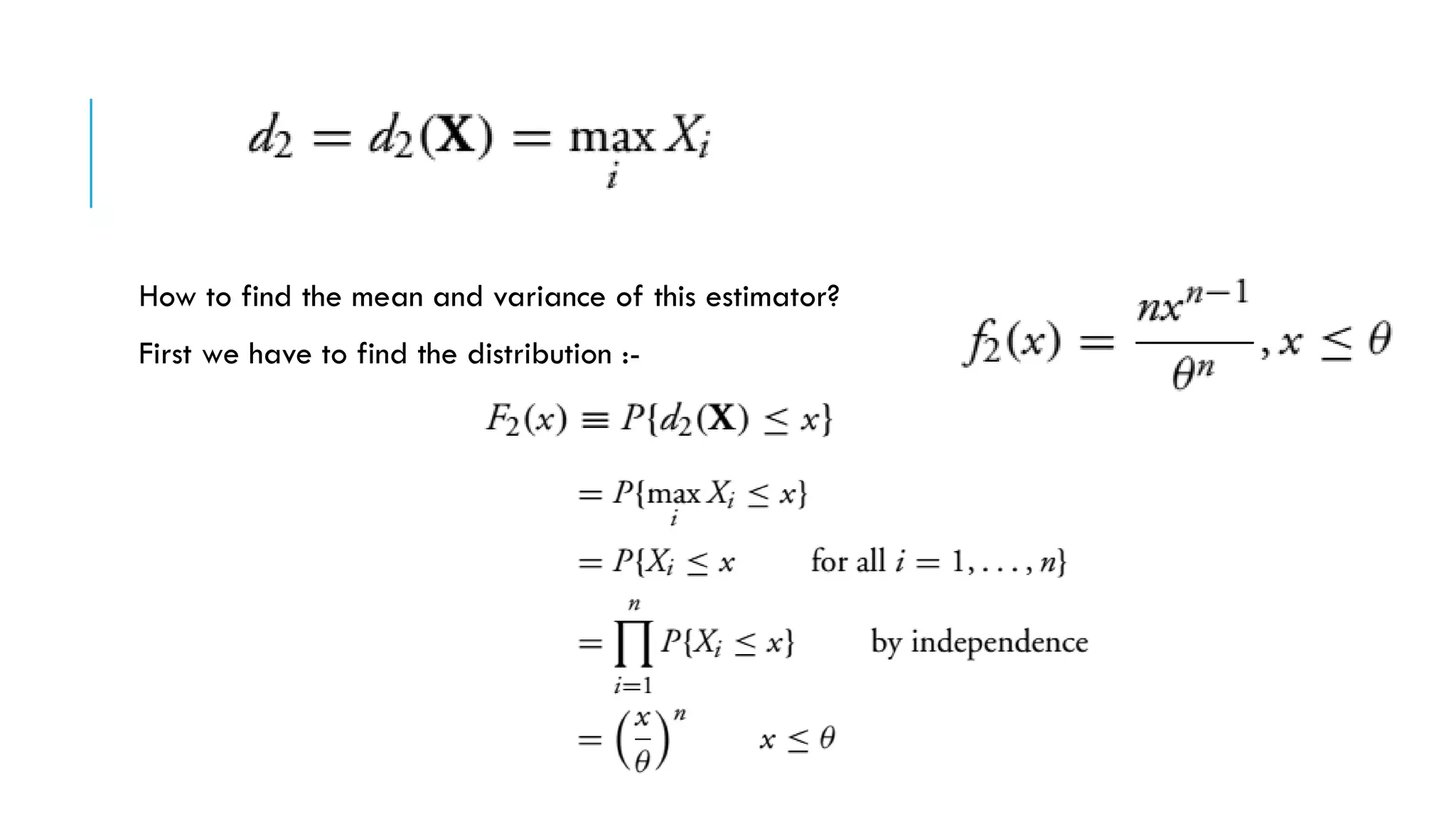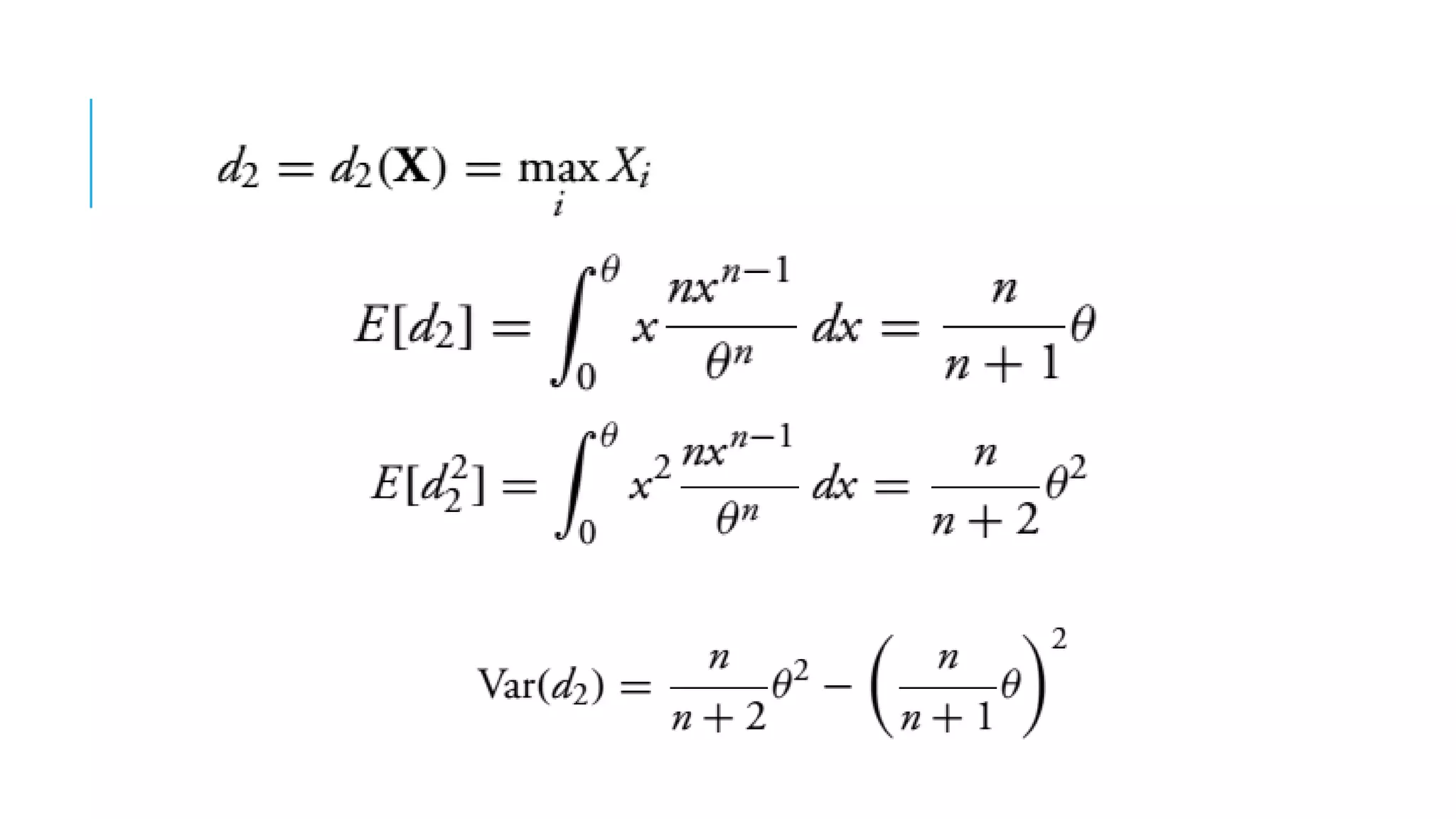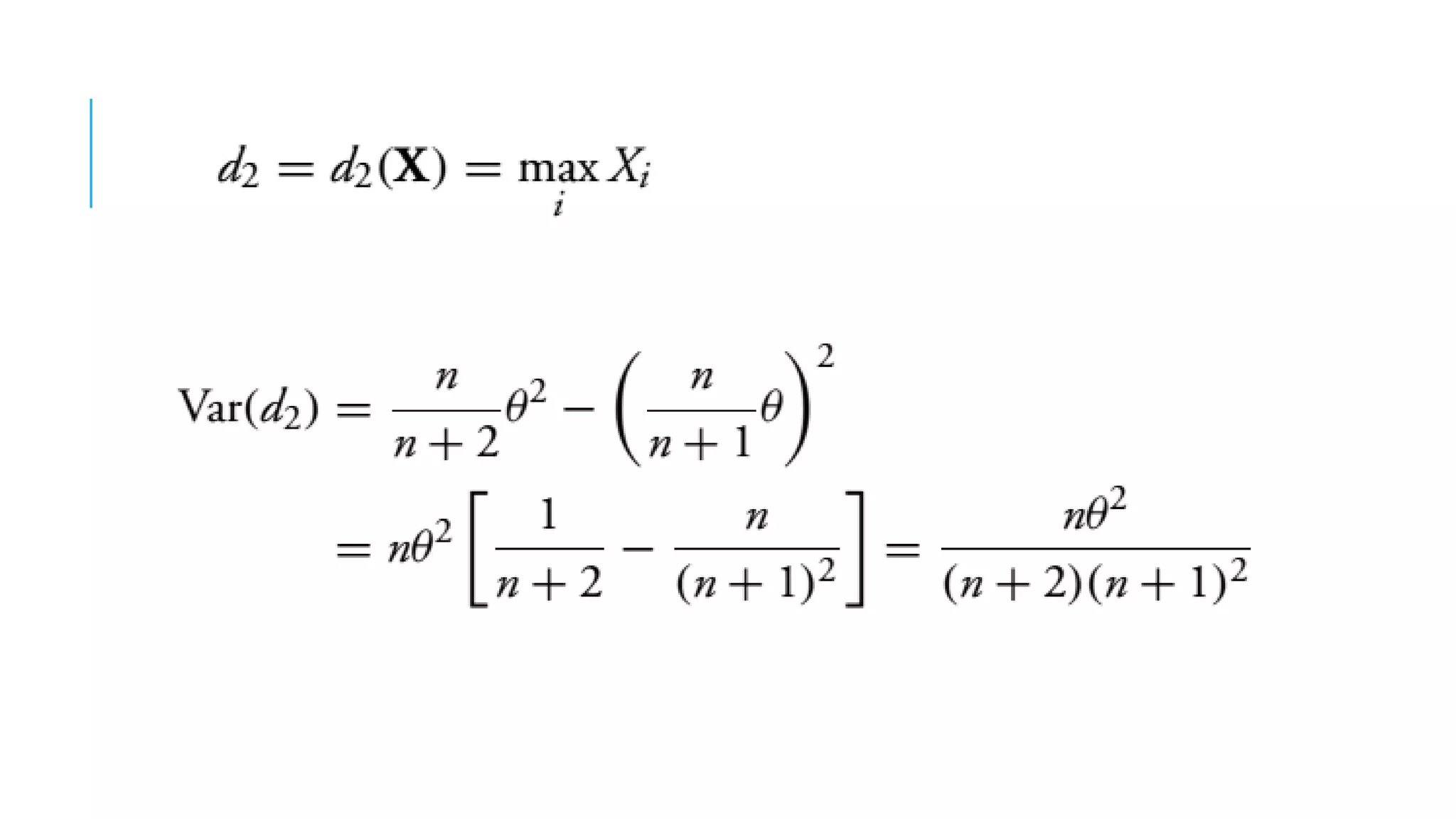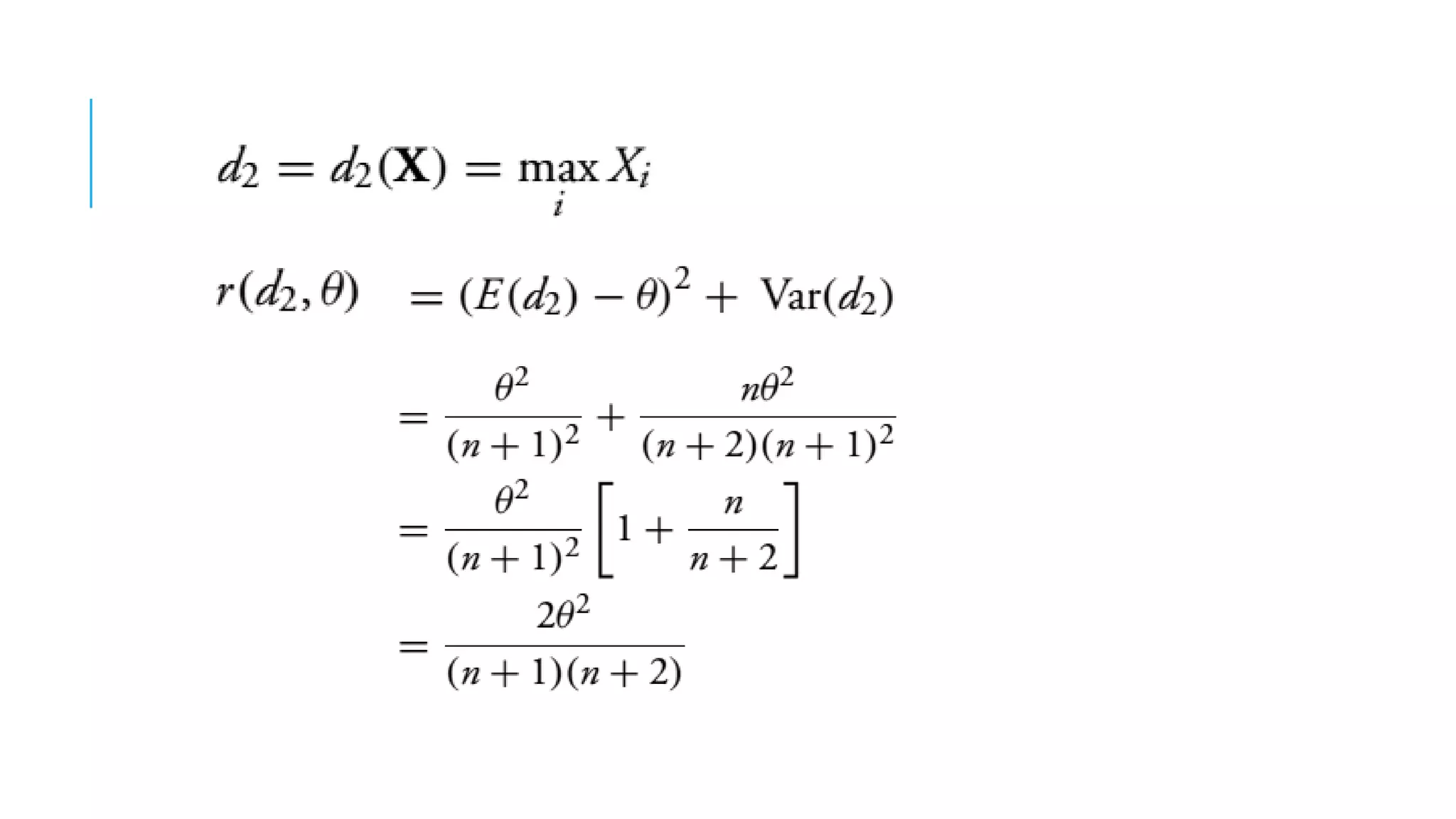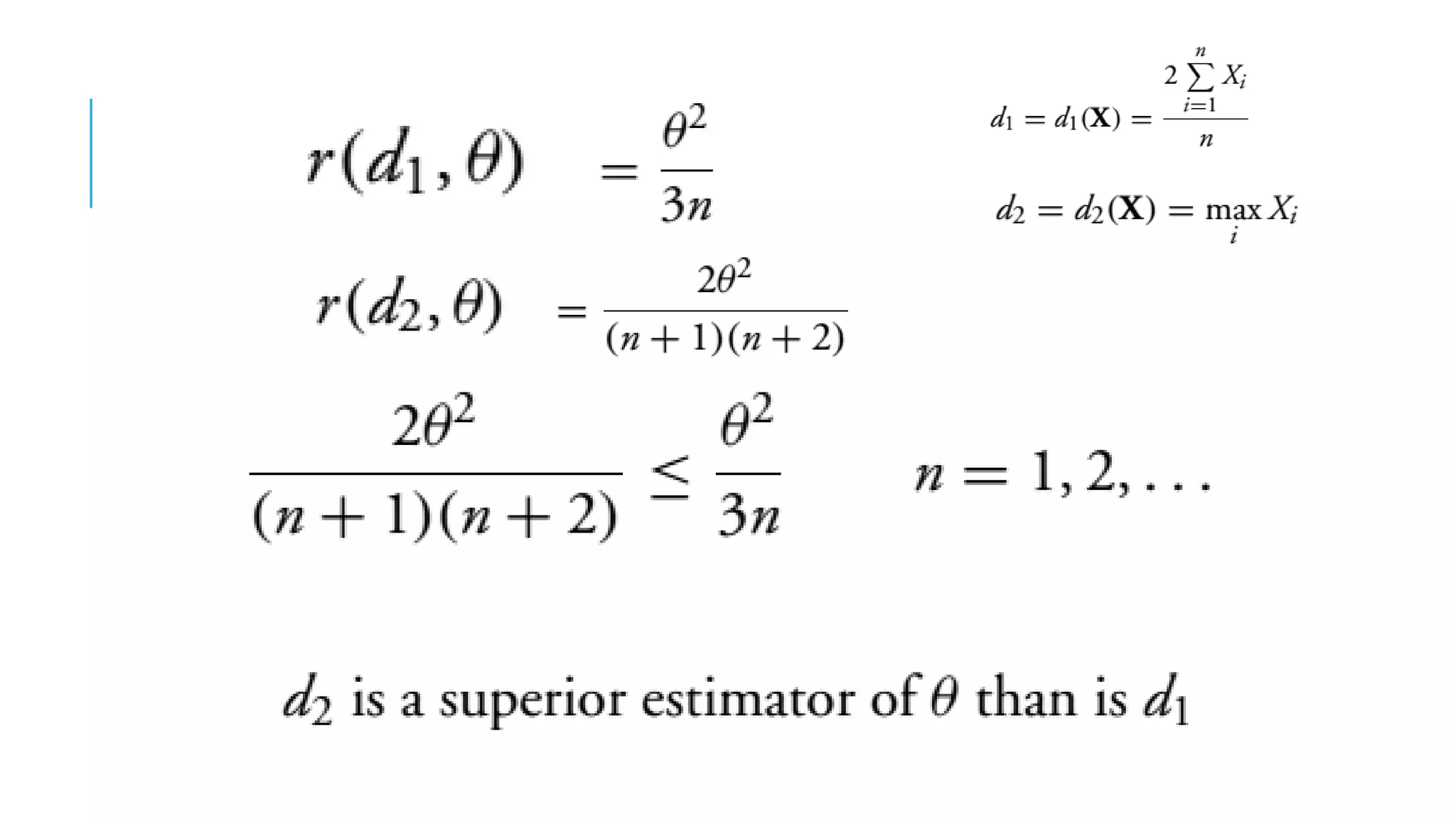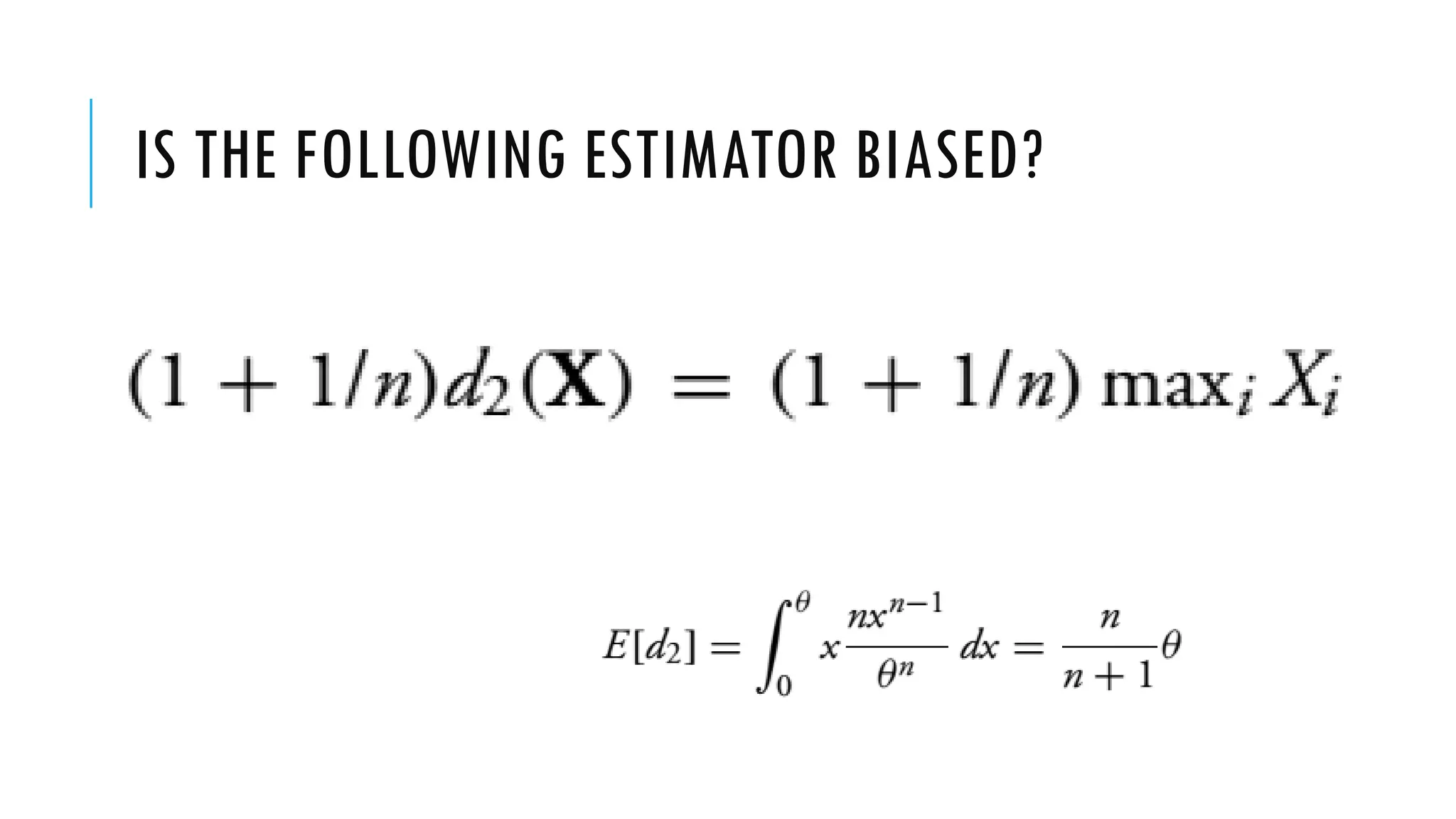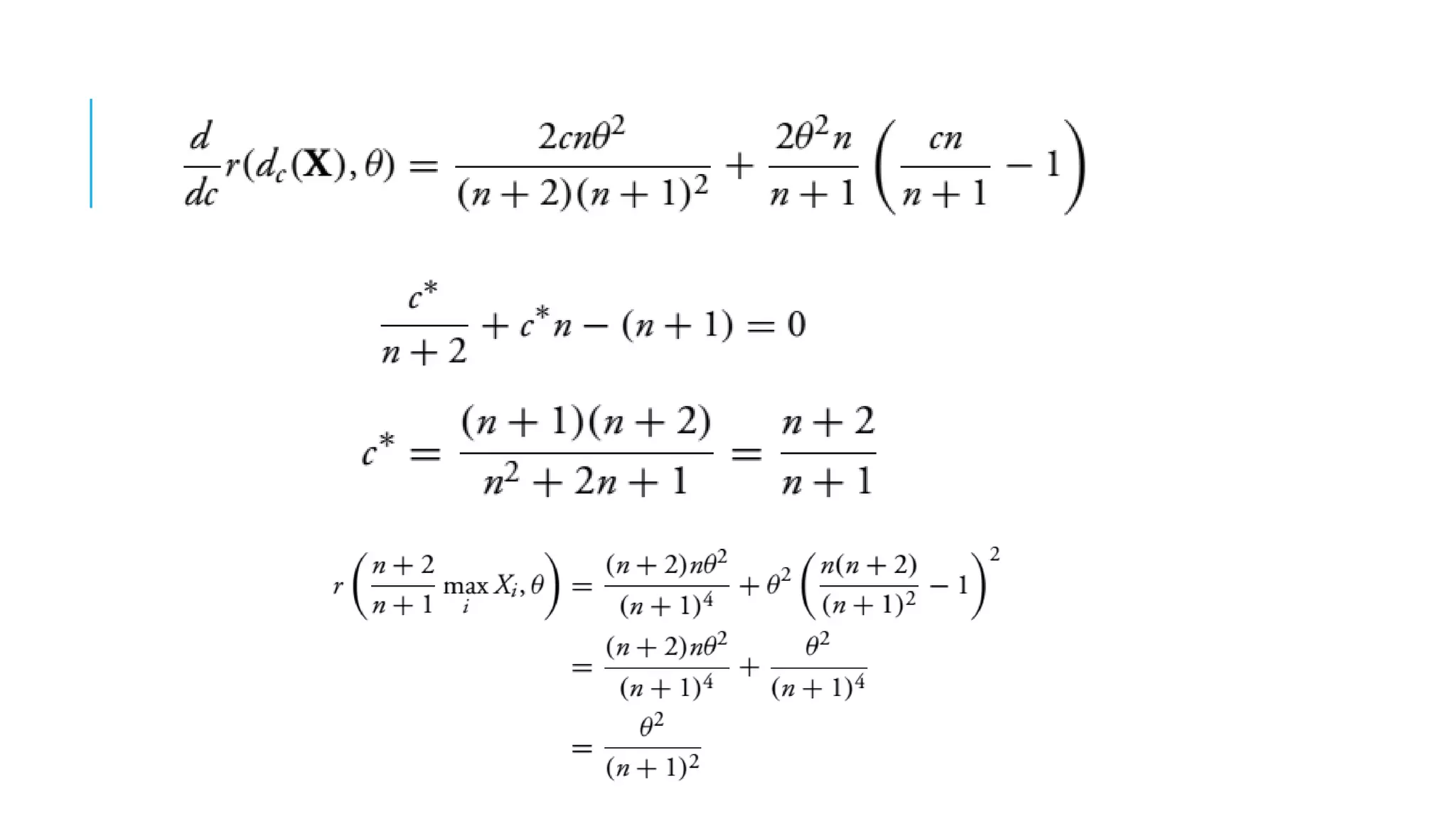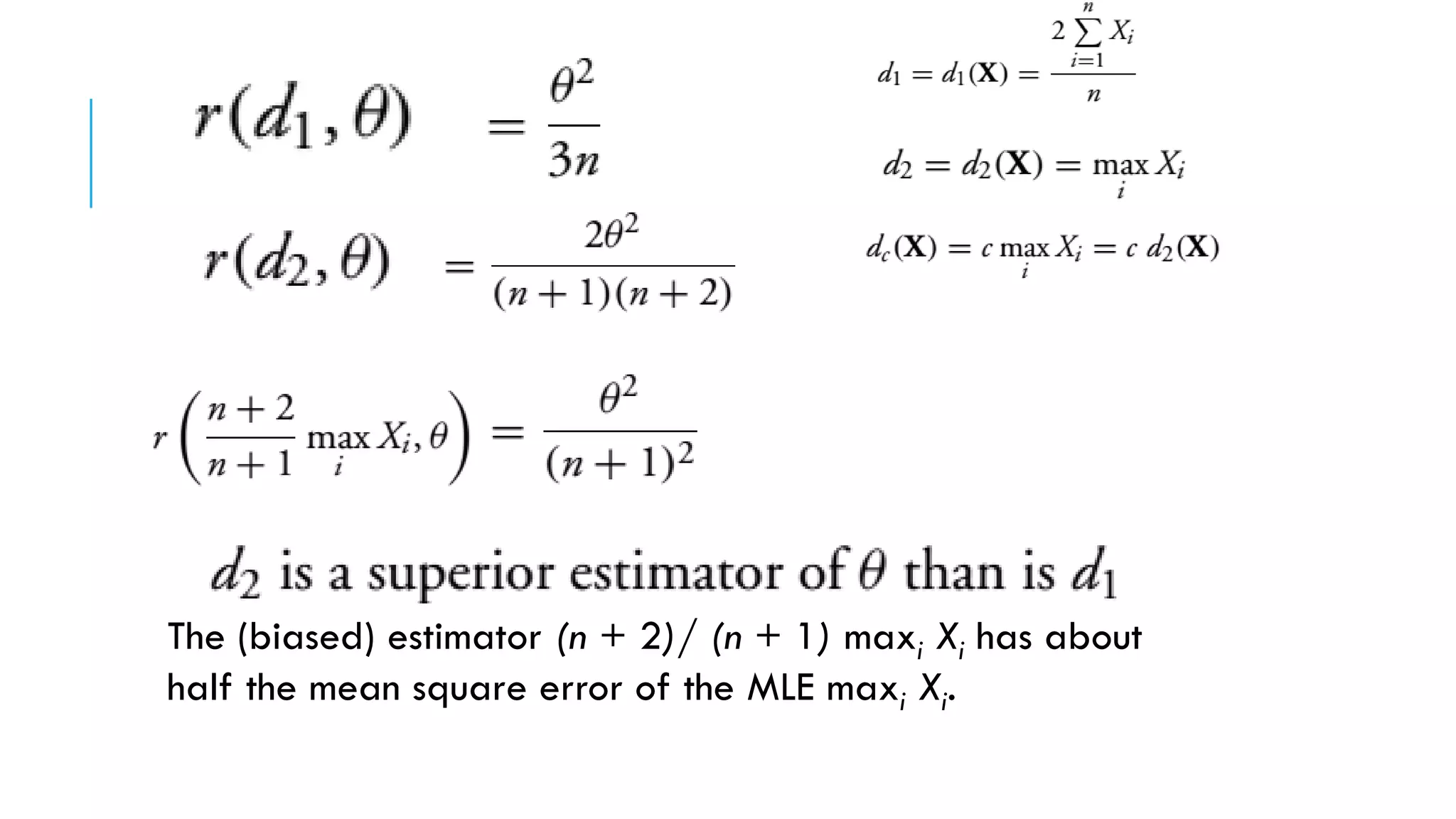This document discusses evaluating point estimators. It defines mean square error as an indicator for determining the worth of an estimator. There is rarely a single estimator that minimizes mean square error for all possible parameter values. Unbiased estimators, where the expected value equals the parameter, are commonly used. Bias is defined as the expected value of the estimator minus the parameter. Combining independent unbiased estimators results in an estimator with variance equal to the weighted sum of the individual variances. The mean square error of any estimator is equal to its variance plus the square of its bias. Examples are provided to illustrate evaluating bias and finding mean and variance of estimators.

1. PARAMETER ESTIMATION Chapter 7

2. EVALUATING A POINT ESTIMATOR
Let X = (X1, . . . , Xn) be a sample from a population whose distribution is
specified up to an unknown parameter θ.
Let d = d(X) be an estimator of θ.
How are we to determine its worth as an
estimator of θ ?

3. EVALUATING A POINT ESTIMATOR
r(d, θ) : the mean square error of the estimator d
An indicator of the worth of d as an estimator of θ
No single estimator d that minimized r(d, θ) for all
possible values of θ.

4. EVALUATING A POINT ESTIMATOR
Minimum mean square estimators rarely exist
Possible to find an estimator having the smallest mean square error among all
estimators that satisfy a certain property.
One such property is that of unbiasedness.
An estimator is unbiased if its expected value always equals the value of the
parameter it is attempting to estimate.
The bias of d as an estimator of θ is defined as below:

5. EVALUATING A POINT ESTIMATOR
Example: Let X = (X1, . . . , Xn) be a sample from a population whose
distribution is specified up to an unknown parameter θ.
Let d = d(X) be an estimator of θ.
Find the bias for the following estimators:

6. EVALUATING A POINT ESTIMATOR

7. EVALUATING A POINT ESTIMATOR

8. EVALUATING A POINT ESTIMATOR
Combining Independent Unbiased Estimators:
Let d1 and d2 denote independent unbiased estimators of θ,
having known variances σ1
2 and σ2
2. For i = 1, 2,
New estimator
from the old
ones

9. EVALUATING A POINT ESTIMATOR
It will be unbiased.
To determine the value of λ that results in d having the smallest possible mean square
error:

10. EVALUATING A POINT ESTIMATOR
The optimal weight to give an estimator is inversely proportional to its
variance (when all the estimators are unbiased and independent).

11. EVALUATING A POINT ESTIMATOR
A generalization of the result that the mean square error of an unbiased estimator is
equal to its variance
is that
the mean square error of any estimator is equal to its variance plus the square of its
bias.

12. EVALUATING A POINT ESTIMATOR

13. EVALUATING A POINT ESTIMATOR
The mean square error of any estimator is equal to its variance
plus the square of its bias

14. EVALUATING A POINT ESTIMATOR
Let X = (X1, . . . , Xn) be a sample from
a uniform distribution (0, θ) with the unknown parameter θ.
Let us evaluate the following estimators:

15. EVALUATING A POINT ESTIMATOR
Is d1 is unbiased?

16. EVALUATING A POINT ESTIMATOR

17. How to find the mean and variance of this estimator?
First we have to find the distribution :-

22. IS THE FOLLOWING ESTIMATOR BIASED?

25. The (biased) estimator (n + 2)/ (n + 1) maxi Xi has about
half the mean square error of the MLE maxi Xi.

26. Thank you for your attention