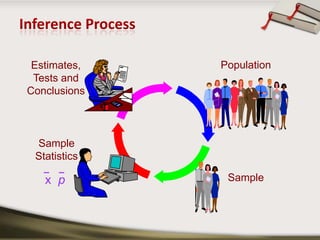
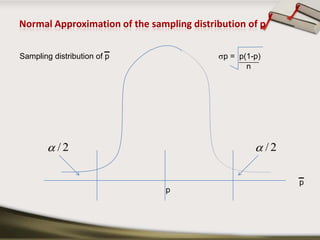
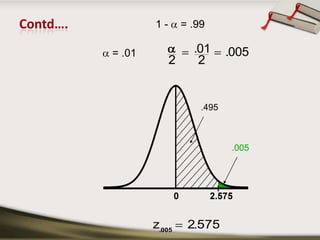
This document discusses interval estimation for proportions. It defines point estimates and interval estimates. A point estimate is a single value of a statistic used to estimate a population parameter, like the sample proportion p estimating the population proportion P. An interval estimate provides a range of values between which the population parameter is expected to lie with a certain confidence level, like a 95% confidence interval for a proportion. Two examples are provided to demonstrate how to calculate a confidence interval for a sample proportion and interpret whether it supports or contradicts a claimed population proportion.

1. Interval Estimation for Proportions

2. Inference Process Population Estimates, Tests and Conclusions Sample Statistics Sample x p

4. confidence interval for proportion

5. sample mean

7. Point Estimate v/s Interval Estimate Interval Estimate = Point Estimate +/- Margin of Error Interval Estimate = p +/- Margin of Error The point estimate is a sample statistic used to estimate the population parameter. For instance, the sample proportion p is a point estimator of the population proportion p. Because the point estimator does not provide information about how close the estimate is to the population parameter, statisticians prefer to use an interval estimate which provides information about the precision of the estimate.

8. Properties p is based on large sample condition that both np and nq are 5 or more.

9. Normal Approximation of the sampling distribution of p Sampling distribution of p sp = p(1-p) _____ n p p

10. Example 1 WE School conducted a class survey to check if they were confident about their Statistics presentations. The survey was conducted on 200 students and it found that 80 students were confident about their Statistics presentations. Thus the point estimate of the proportion of the population of students who were confident about their presentation is 80/200 = 0.4 Using 95% confidence interval, we have

11. Contd…. Therefore, = 0.4 – 1.96 * 0.034641 < p < 0.4 + 1.96 * 0.034641 = 0.4 - 0.067896 < p < 0.4 + 0.067896 = 0.332104 < p < 0.467896 Thus the margin of error is 0.067896 and the 95% confidence interval estimate of the population proportion is 0.332104 to 0.467896. Using percentages, the survey results enable us to state that with 95% confidence between 33.21% and 46.78% of all students are confident about their Statistics presentations.

12. Example 2 The Peacock Cable Television Company thinks that 40% of their customers have more outlets wired than they are paying for. A random sample of 400 houses reveals that 110 of the houses have excessive outlets. Construct a 99% confidence interval for the true proportion of houses having too many outlets.

13. Contd….. Do you feel the company is accurate in its belief about the proportion of customers who have more outlets wired than they are paying for? X = number of houses that have excessive outlets = 110, n = 400, and the confidence level = .99. Thus,

14. Contd…. .495 .005 1 - a = .99 a = .01

15. Contd…. A 99% confidence interval for the true proportion of houses having too many outlets is given by

16. Contd…. Interpretation: We are 99% confident that the true proportion of houses having too many outlets is between .2175 and .3325. Note: We do not believe that 40% of customers have more outlets wired than they are paying for because we are 99% confident that the true proportion is in the interval 21.75% to 33.25% and 40% isnot in that interval.

18. AdityaMahagaonkar

19. Priya Bhattacharya

20. ParagDhake

21. TanviShenoy