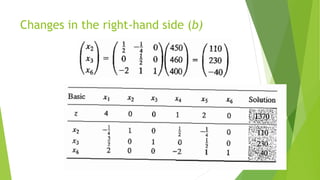
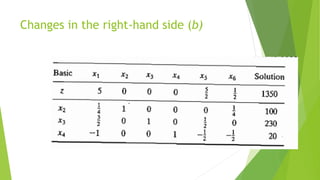
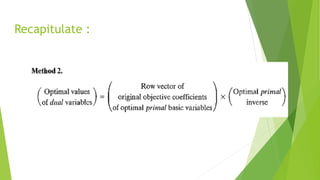
The document discusses post-optimal analysis in linear optimization problems. It describes how changes can affect feasibility or optimality, including changes to right-hand sides, adding new constraints, or changing objective coefficients. It also discusses adding a new activity/variable and using the dual simplex method to find the new optimal solution.

1. Post-Optimal Analysis
Linear optimization problem

2. Contents
Introduction to Post-Optimal Analysis
Changes Affection Feasibility
Changes in the right-hand side (b)
Addition of a new constraint
Changes Affecting Optimality
Changes in the Objective Coefficients (c_j)
Addition of new activity (x_j)

3. Post-Optimal Analysis
The sensitivity of the optimum solution
By determining the ranges for the different LP parameters that keeps the optimum basic variable unchanged
Deal with making changes in the parameters of the model and finding the new optimum solution
These changes require periodic re-calculation of the optimum solution and
The new computations are rooted in the use duality and the primal-dual relationships

4. Post-Optimal Analysis

5. Example : Assembling 3 types of toys

6. Example : Assembling 3 types of toys
Optimum tableau for the primal is

7. Changes Affection Feasibility
Two possibilities which can affect feasibility are
Changes in the right-hand side (b)
A new constraint is added

8. The dual problem uses exactly the same parameters as the primal problem, but in
different location.
Primal and Dual Problems
Primal Problem Dual Problem
Max
s.t.
Min
s.t. 

n
j
j j Z c x
1
, 

m
i
i i W b y
1
,


n
j
ij j i a x b
1
, 

m
i
ij i j a y c
1
,
for for i 1,2,,m. j 1,2,,n.
for
i 1,2,,m.
for  0, j 1,2,,n. j x  0, i y
RHS means

9. Changes in the right-hand side (b)

10. Changes in the right-hand side (b)
New RHS of the problem
The current basic variable remain feasible at the new values and
The optimum revenue is $1880

11. Changes in the right-hand side (b)

12. Changes in the right-hand side (b)

13. Addition of a new constraint
The new constraint for the operation 4 is
3x1 +3x2 + x3≤ 500

14. Addition of a new constraint

15. Addition of a new constraint

16. Addition of a new constraint
The tableau shows the x7 = 500 which is not consistent with the values of x2 and x3 in the rest of the table….
Reason: the basic variable x2 and x3 have not been substituted out in the new constraint…

17. Addition of a new constraint
Application of the dual simplex method will produce the new optimum solution
x1 = 0, x2 = 90, x3 = 230, and z = $1370 (verify!)

18. Changes Affecting Optimality
The changes in the Objective Coefficients
The addition of a new economic activity (variable)

19. Changes in the Objective Coefficients

20. Changes in the Objective Coefficients
Affect only the optimality of the solution and require recomputing the z-row coefficients (reduced costs):-
1)Compute the dual values using the Method 2
2)Substitute the new dual values in Formula 2, to determine the new reduced costs (z-row coefficients).

21. Recapitulate :

22. Recapitulate :

23. Changes in the Objective Coefficients
Maximize z = 2x1+ 3x2+ 4x3is the new objective function then,

24. Changes in the Objective Coefficients
Maximize z=
2x1+
3x2+
4x3

25. Changes in the Objective Coefficients
Maximize z = 6x1+ 3x2+ 4x3is the new objective function then,

26. Changes in the Objective Coefficients
The optimum solution :-x1 = 102.5 x2 = 215 and z = $12270.50 (verify)

27. Addition of new activity

28. Addition of new activity
A new activity signifies adding a new variable to the model
Intuitively, the new activity desirable only if it is profitable
Formula 2 will help in checking this
To compute the reduced cost of the new variable
Let x7 represents the new product in the TOYCO and
Revenue per new toy is $4
Operation 1 1 minute
Operation 2 1 minute
Operation 3 2 minutes
The new column in the coefficient matrix of the constraints
4x_7 will be the extra term in the primal objective function

29. Addition of new activity
Given that (y_1, y_2, y_3) = (1,2,0) are the optimal dual variable,
Reduce cost of x7 is

30. Addition of new activity
Not Optimal but feasible solution
The new optimum is obtained by letting x7 enter the basis and x6 must leave the basis…..
The new optimum is x1 = 0, x2 = 0, x3 = 125 and x7 = 210 with the revenue z = $1465 (verify)

31. Thanks for your attention