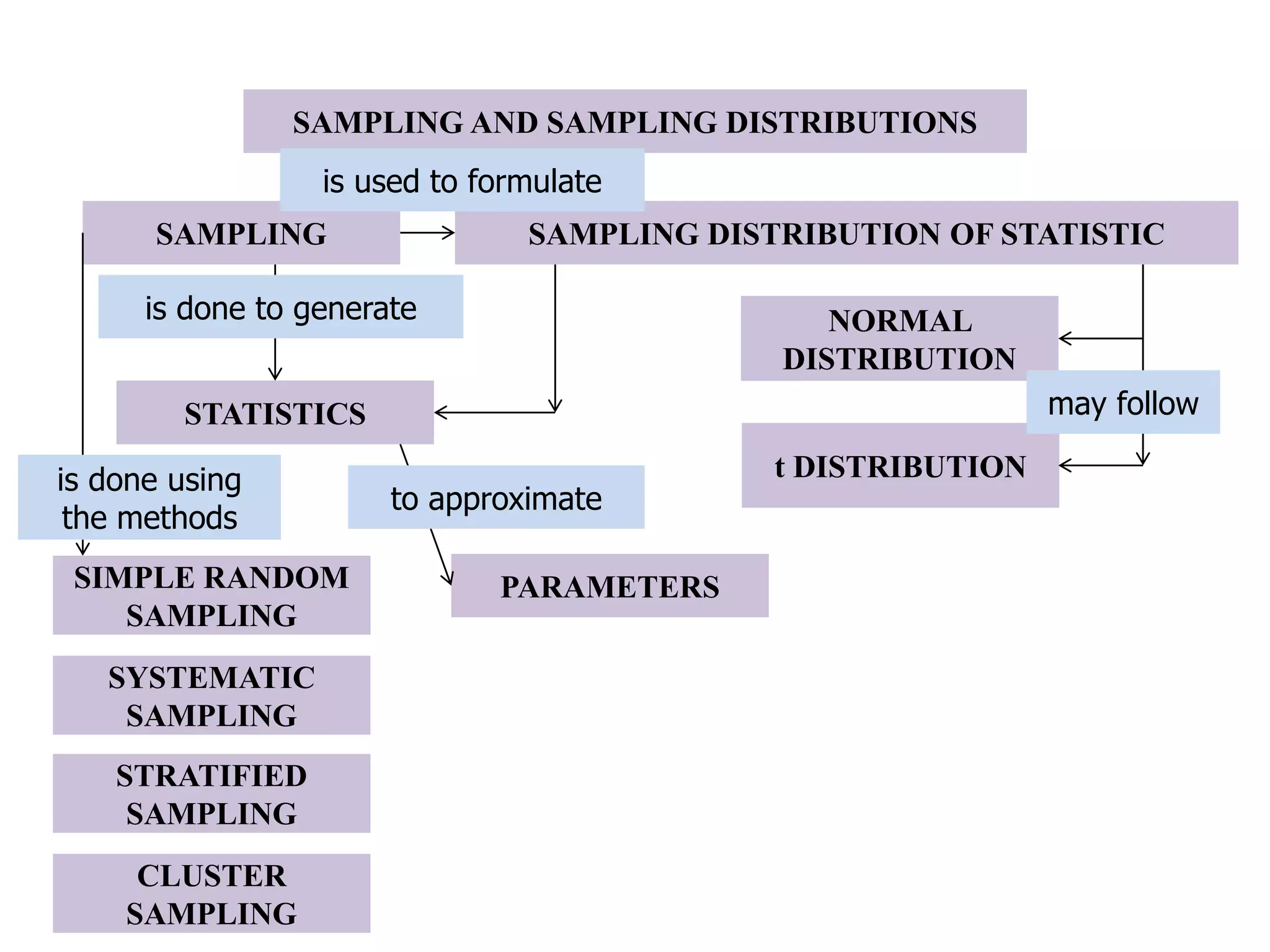
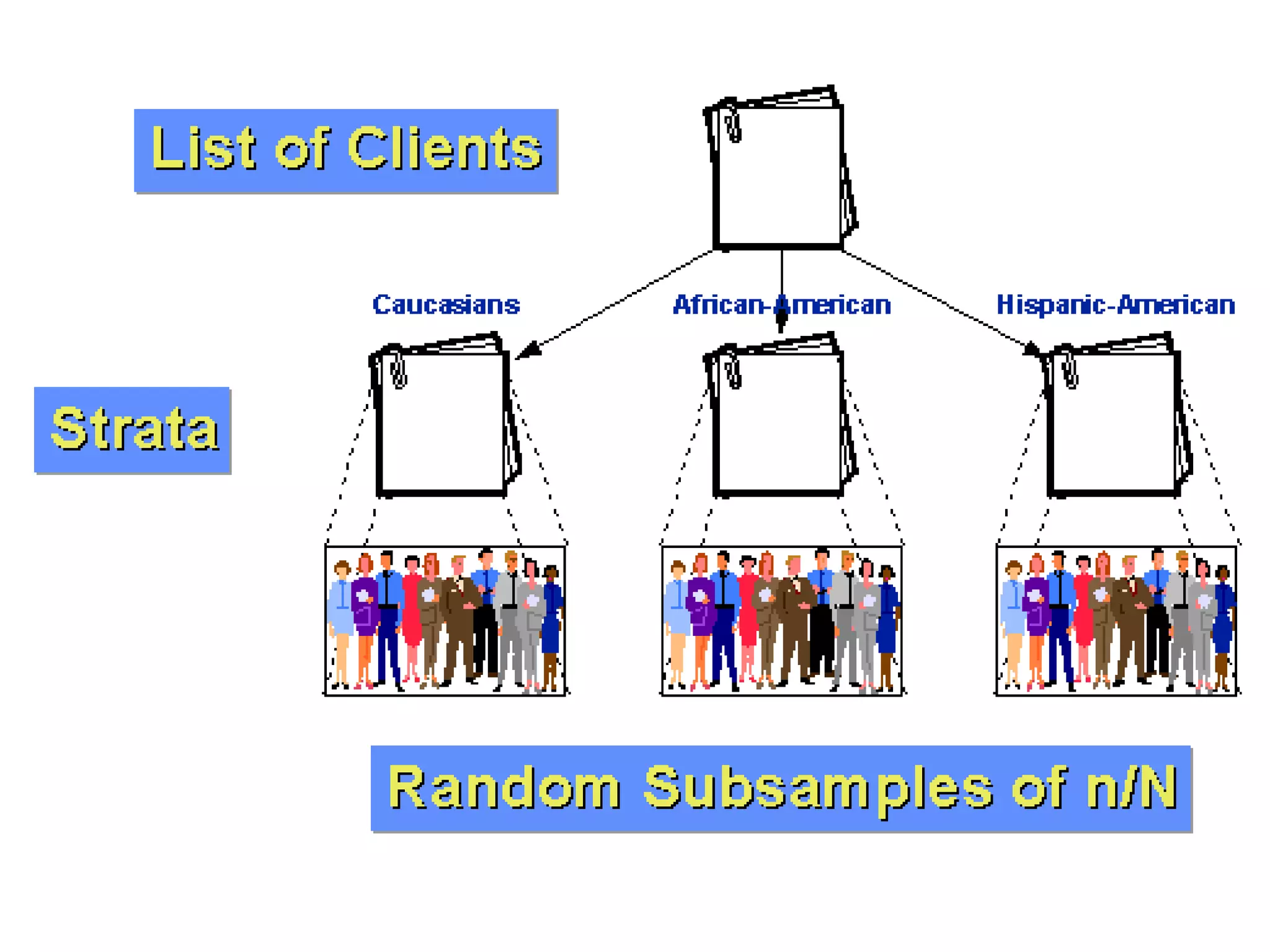
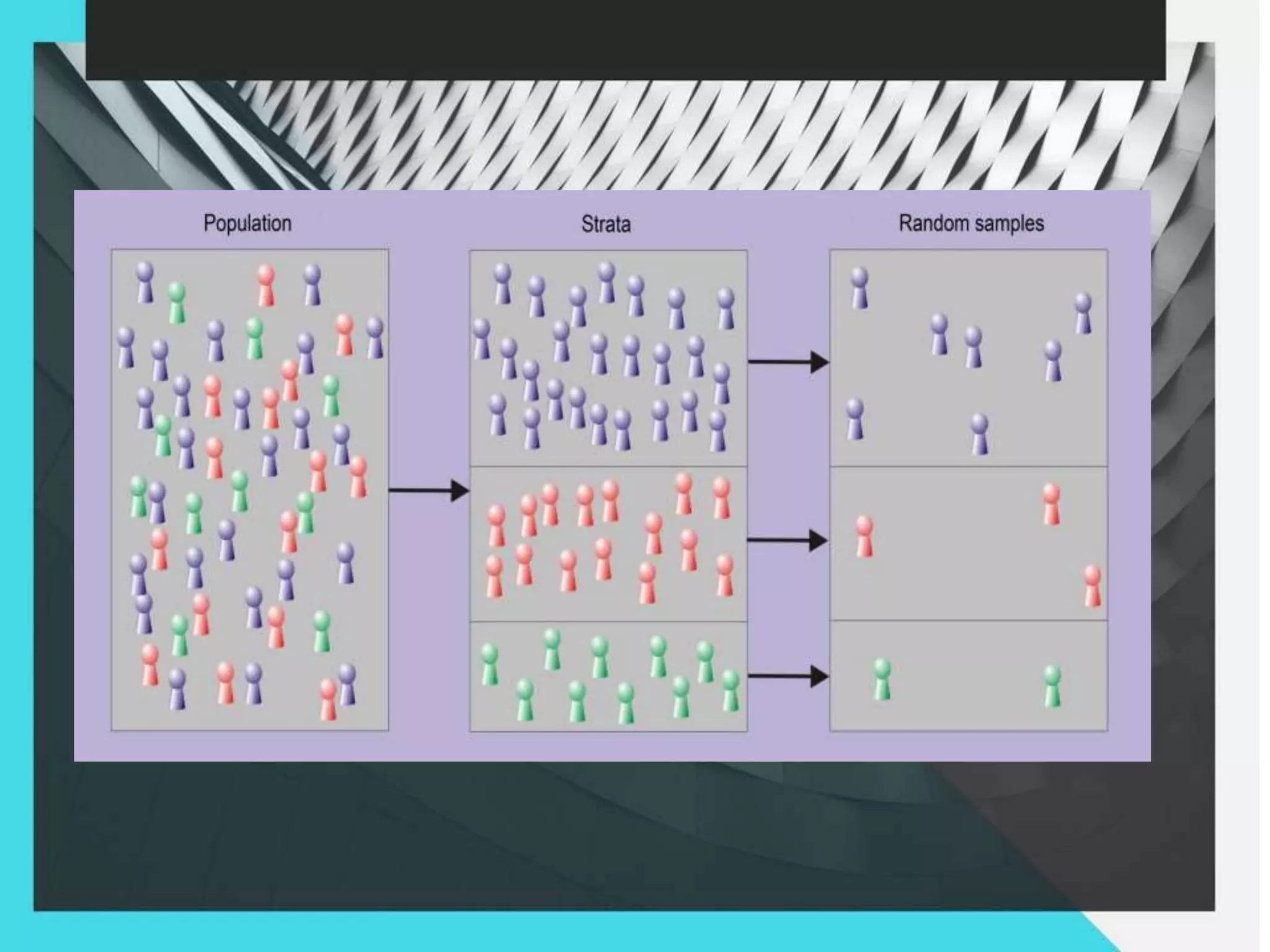
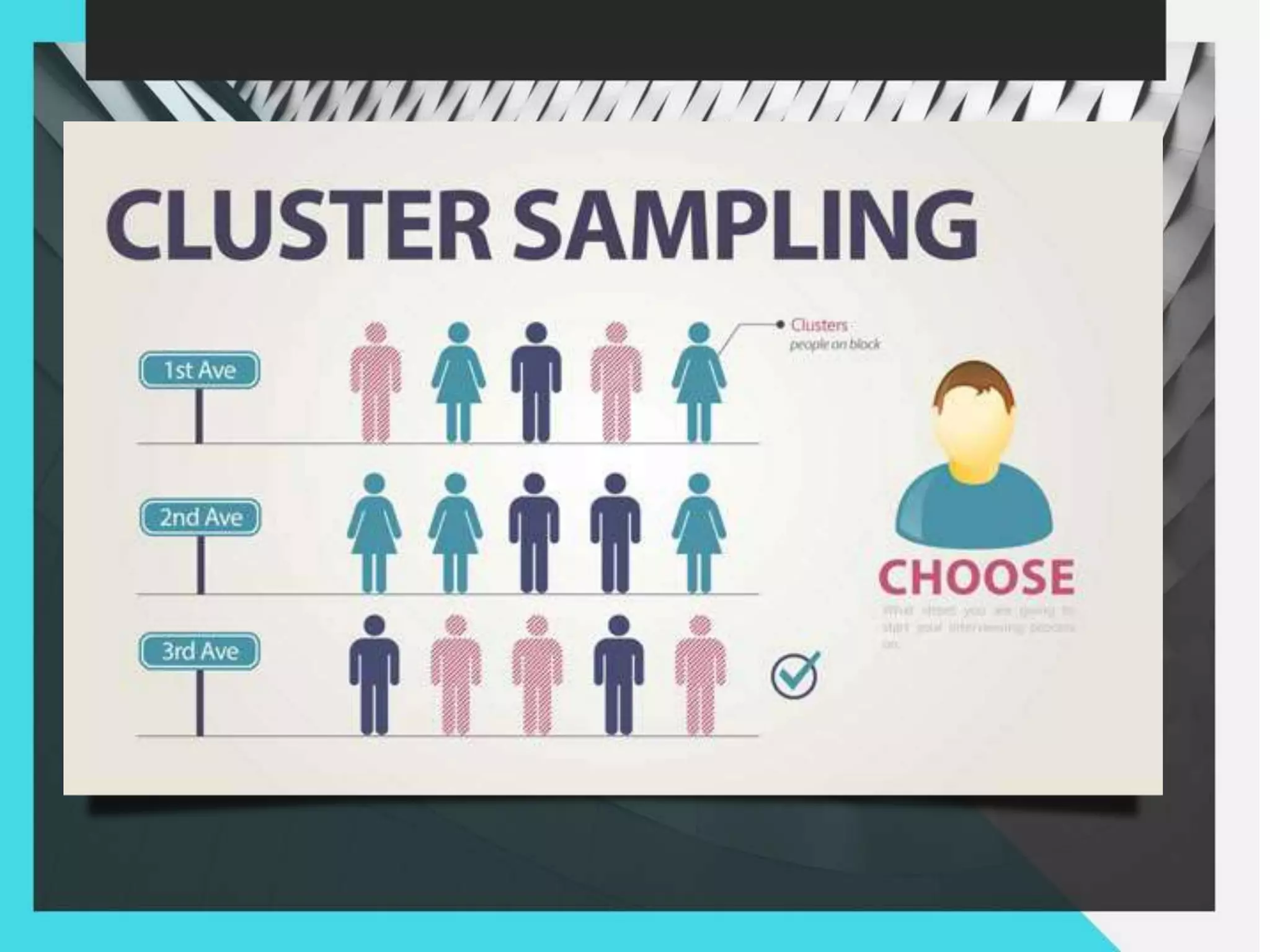
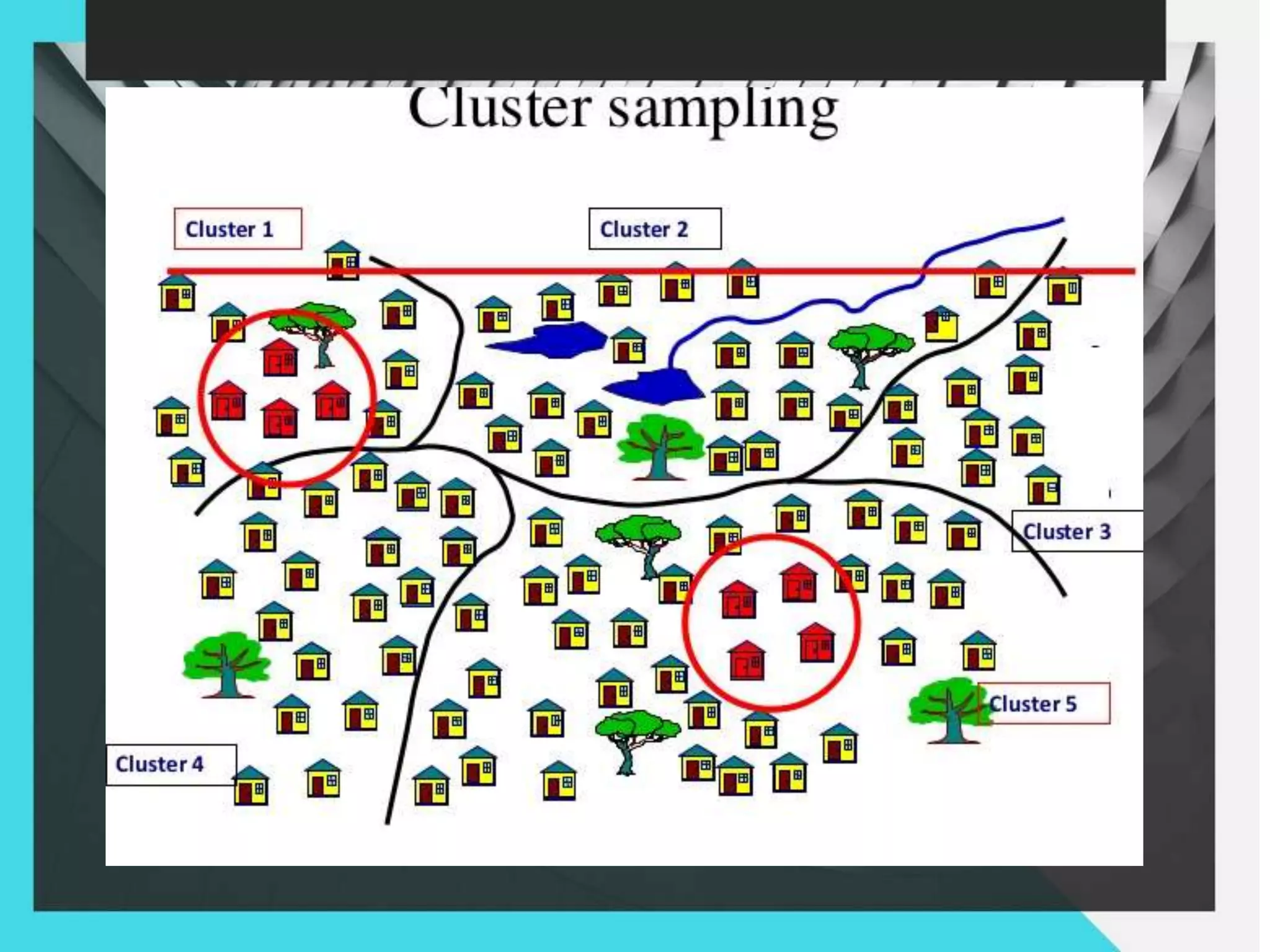
1. The document discusses different sampling methods including simple random sampling, systematic random sampling, stratified sampling, and cluster sampling. 2. It provides examples of how each sampling method works and how samples are selected from the overall population. 3. Exercises are provided to determine which sampling method should be used for different scenarios involving selecting samples from identified populations.

2. What is a sample? Why
study it?

3. SAMPLING
- the method of gathering
information about a population by
taking a representative of the
population called sample

4. Can the data gathered from the
sample be used to make
inferences about the
population?

5. Statistically speaking,
yes.

6. However, every sample has a different
statistic. And this statistic is also
considered a random variable because
the data vary from one sample to
another.

7. SAMPLING AND SAMPLING DISTRIBUTIONS
SAMPLING SAMPLING DISTRIBUTION OF STATISTIC
STATISTICS
PARAMETERS
NORMAL
DISTRIBUTION
t DISTRIBUTION
SIMPLE RANDOM
SAMPLING
SYSTEMATIC
SAMPLING
STRATIFIED
SAMPLING
CLUSTER
SAMPLING
is used to formulate
is done to generate
to approximate
may follow
is done using
the methods

8. SAMPLING
METHODS

9. 1. Simple Random Sampling
2. Systematic Random Sampling
3. Stratified Sampling
4. Cluster Sampling

10. SIMPLE RANDOM
SAMPLING

11. - involves selecting a sample size n
from a population of size N so that
all elements of the population have
equal chances of being part of the
sample.

12. • lotteries
• tables of random numbers
• automatic random number generator

17. SYSTEMATIC
RANDOM
SAMPLING

18. - involves using a random start to
determine the first element of the
sample and the selection of the rest of
the sample is done systematically, i.e.,
every kth interval, where k = N/n.

21. STRATIFIED
SAMPLING

22. - involves dividing the population into
groups called STRATA according to
some chosen classification category
such as age, gender, geographic
location, and so on. Subsample from
each stratum are selected by simple
random sampling.

25. CLUSTER
SAMPLING

26. - the elements of the population are
divided into groups called
CLUSTERS. Clusters are naturally
occurring like barangays, cities, or
municipalities. Samples are obtained
from each cluster by SRS.

29. SLOVIN’S FORMULA
- Used to calculate the sample size n
given the population size N and a
margin of error e.

30. Slovin's formula is used
when nothing about the
behavior of a population is
known at all.

35. EXERCISES
Determine the sampling method to
be used in each scenario.

36. EXERCISES
Determine the sampling method to
be used in each scenario.

37. 1. From a list containing the names
of 500 members of an alumni
association, a sample size of 50 is
obtained by including every 10th
person in the list in the sample.

38. 2. The students in a given school
are classified according to grade
level. Twenty students from each
group will be randomly chosen to
participate in a study involving
students’ study habits.

39. 3. All the students who belong to
ten chosen sections in a certain
school will participate in a study
designed to improve students’
critical thinking skills.

40. 4. A researcher is interested in studying
the effects of diet on the attention span
of third-grade students in a large city.
There are 1,500 third-graders attending
the elementary schools in the city. The
researcher selects 150 of these third-
graders, 30 each in five different
schools, as a sample for study.

41. 5. An administrator in a large urban high school is
interested in student opinions on a new counseling
program in the district. There are six high schools
and some 14,000 students in the district. From a
master list of all students enrolled in the district
schools, the administrator selects a sample of
1,400 students (350 from each of the four grades,
9–12) to whom he plans to mail a questionnaire
asking their opinion of the program.

42. 6. The principal of an elementary school
wants to investigate the effectiveness of a
new U.S. history textbook used by some of
the teachers in the district. Out of a total of
22 teachers who are using the text, she
selects a sample of 6. She plans to compare
the achievement of the students in these
teachers’ classes with those of another 6
teachers who are not using the text.

43. ACTIVITY

44. Using the members of your class as the
population, use AGE as the quantitative
variable of interest and obtain a sample size
of 10 using the four sampling techniques.
Calculate the sample mean age (statistics)
of your data and compare it with the
population mean (parameter). Do this by
triads in a one whole piece of paper.

45. QUESTION: Which of the four
sampling techniques produced
statistics which is closest to the
population parameters?
farthest? What does this imply?